Section 2-3 - Capacitors, Capacitance, and Dielectrics

Capacitors & Capacitance
Parallel Plate Capacitors
Dielectrics
Energy Stored in a Capacitor
Combinations of Capacitors
Correlation to your Textbook

Capacitors & Capacitance

A capacitor can be defined as an device to store charge.  Usually, while storing the charge, it also stores energy.  Here is a very simple example: consider an initially uncharged metal sphere of radius R.  Let's bring a very small bit of charge from infinity to the metal, where it will of course reside on the surface.  Now, the sphere is slightly charged.  To bring the next bit of charge up from infinity, some work must be done to overcome the repulsion it experiences due to the first bit of charge.  The third bit of charge will require even more work, et c.  This energy is stored as the electrical potential energy  of the charges.  Accordingly, the electrical potential at the surface of the sphere increases, as well.

The ability of a capacitor to hold charge is characterized by the capacitance, C.  Specifically, we say that the capacitance is the amount of charged transferred on the capacitor per volt of potential difference:
C = Q/V.
The unit of capacitance is the farad (F), named after Michael Faraday (The faraday was already a unit used by chemists).

What, then, is the capacitance of the metal sphere described above?


Once charged, the potential field caused by the charge will look like that of a point charge: V = keQ/r.  At the surface of the sphere (where r = R), the potential will then be V = keQ/R, where we define the potential at infinity to be zero.  Then,
C = Q/V = Q/[keQ/R] = R/ke.
Note that we generally (but not necessarily) think of capacitors as having two plates, with the charge taken from one and placed on the other.  In this example, one might consider the second plate to be located out at infinity.

Parallel Plate Capacitors

Let's look at a very special type of capacitor, the parallel plate capacitor.  This comprises two flat, parallel, probably metal, sheets of area A separated by a relatively small distance d.  Let's transfer a charge Q from one plate to the other, causing a potential difference V; now one plate has charge +Q and the other -Q.  We can, if we like, talk about the charge per unit area, s = Q/A.  From this, we get the notion that each plate resembles to some degree an infinite sheet of charge like those discussed in the Gauss's Law section of the notes; we can get away with this if the separation of the plates is small compared to the length of a side.  In that case, the positive sheet creates an electric field of magnitude E+ = s/2eo outward, while the negatively charged sheet produces a field of magnitude E- = s/2eo inward.  In the region between the sheets, these fields will add to give a total field of E = s/eo, and in the outer regions, the fields will cancel.

Let's look at the definition of capacitance again:
C = Q/V.
Do some substitution, remembering that E = (-)DV/Ds(here Ds will be the distance between plates, d):
C = Q/V = sA/V = sA/Ed = sA/(s/eo)d = eoA/d.

We see that the capacitance of a parallel plate capacitor depends only on the dimensions of the capacitor, plus some constant that makes the units work out.  For different configurations, the specific result will be somewhat different, but still based on the dimensions only.  The nice result is that, for a situation such as this, the capacitance of the capacitor is a constant regardless of the amount of charge it holds.  This is not always true; special capacitors have been built with new materials from which C can vary with an additional applied voltage.
 

Here's another example.  Calculate the capacitance of two concentric cylinders of radiuses R1 and R2 and length L.  Assume that L is long compared to the radiuses.


If the cylinders are long, we can make use of the expression for the electric field we found in the previous section (assume the inner cylinder R1 is positive)
E = 2kel/r.
DV = - R1R2 E.dr = - R1R2 2kel/r dr = - 2kel ln[R2/R1].  Ignore the negative sign for now; it indicates that the potential is lower on the outer cylinder .
Then, C = Q/DV = lL/[2kel ln[R2/R1]] = L/[2ke ln[R2/R1]].
This result again depends only on the dimensions of the capacitor.

Let's go back to out original example, but let's have two spheres of radiuses R1 (inner) and R2 (outer).  The field is
E = keQ/r2.
Then,
DV = - R1R2 E.dr = - R1R2 keQr-2dr = keQ[1/R2 - 1/R1] (which is again a negative number).  Ignore the negative sign for now; it indicates that the potential is lower on the outer sphere.
Then, C = Q/DV = Q/[keQ[1/R1 - 1/R2]] = R1R2/ke[R2 - R1]

In the parallel plate and coaxial cylinder examples, we assumed that the E-field was uniform (first case) or radial (second example).  However, when you mapped out the electric field for aprallel plates in your lab exercise, you found that the field bulged out near the ends of the plates. These edge effects can be neglected if the plate separation is small.

Dielectrics

We recall a discussion about the effects of an electric field on metals; the external field casues the charges inside the metal to re-distribute themselves (thus causing an internal field) until the total internal field is zero.  Here, we introduce materials known as dielectrics.  In these materials, the electrons are not as free to move about as those in metals, and so the external field is not completely cancelled, resulting in not a zero net field, but a reduced net field.  The degree to which the material reduces the field is characterized by the dielectric constant, k, such that
E = EEXT/ĸ.

What is the dielectric constant of vacuum?


In a very naive sense, what might one say is the dielectric constant of a metal?

How does the dielectric affect the capacitance of a capacitor?  Insert a slab of dielectric material into the gap between the plates of a parallel plate capacitor, filling the space completely.  Repeat the calculation above.  Then,
C = Q/V = sA/V = sA/Ed = sA/(EEXT/k)d = ksA/(s/eo)d = keoA/d = k Co
That is, the dielectric material increases the capacitance by a factor k. Although we just did this for a parallel plate capacitor, the result is the same for any shape, since E is reduced by factor k, so then so is DV, and so C is incresed by factor k.

LAB EXERCISE: Find the dependence of capacitance on plate area and plate separation for a parallel plate capacitor.

Energy Stored in a Capacitor

When we spoke about transferring the charge from one plate to the other, we mentioned that very little if any energy was required to move the very first electron, but that slightly more was necessary for the next, since we need to pull it away from now positive plate and force it onto the other plate, which is now negatively charged.   In fact, each additional charge we transfer will be harder to move than the preceeding one.  Let's see if we can calculate how much total work is necessary to charge up a capacitor.
First, regard the figure, which shows the relationship between the charge transferred and the potential difference between the plates:

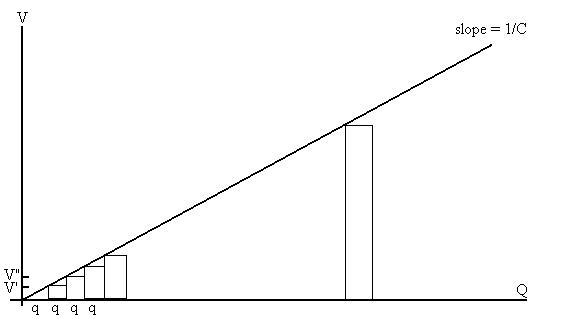
The first q is transported against a zero potential difference, so no work is done, and no energy is stored.  However, in the process, the potential difference is raised to V'.  When the next q is transported, work qV' is done.  This is represented by the area contained by the small rectangle.  When the next charge q is moved, it's moved against a potential difference of V", and the work required is qV", once again represented by the area inside that rectangle.  Once we move the last charge (at potential V, for a total of Q), the total work should be the sum of the areas of all the rectangles.  If we make the size of the charges we moved smaller and smaller, and consequently, the number of them moved larger and larger, the sum of the rectangles' areas should be very close to the area under the triangle,
Wtotal = 1/2(base)(height) = 1/2(Q)(V).
Since work is a transfer of energy, we see that there is now energy stored in the capacitor.
UC = 1/2(Q)(V) = 1/2Q2/C = 1/2CV2.
Alternatively, we can use calculus:
UC = W = 0Q V(q) dq = 0Q [1/C]q dq = 1/2q2/C 0|Q = Q2/2C, as before.

Another quantity that is often considered useful is the energy density, ηE.  Consider the parallel plate capacitor (and ignore edge effects).  The energy stored in the capacitor is 1/2CV2.  The volume of the capacitor is Ad.  The energy per unit volume is then
ηE = 1/2CV2/Ad = 1/2[eoA/d]V2/Ad = eoV2/2d2 = 1/2 eoE2.
The idea here (which I personally don't care for) is that  the electric field itself possesses some energy.  It's sometimes useful.

Combinations of Capacitors

Consider two capacitors connected as shown:

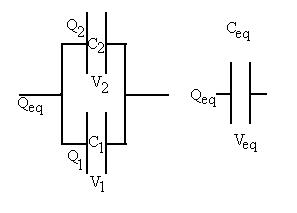
We want the equivalent capacitor on the right to do the same job as the combination on the left: store the same amount of charge Qeq with the same applied potential difference Veq.  What do we know?  By conservation of charge, we know that
Qeq = Q1 + Q2,
since that charge is split between the two capacitors as it is sent in from the left/taken off to the right.
We can also say that
Veq = V1 = V2,
since the potential is related to the work done taking a test charge from one side of the combination to the other, and since the electric field is a conservative field, that work must be independent of the path taken.
 
 
Delving into this a little more deeply, when everything is in equilibrium, the metal wires are equi-potential surfaces, so if the left hand side of the capacitor's wire is at potential VA, then every spot on that wire and the plate itself is also at potential VA.  The same is true for the other end, which we might say is at potential VB; every point on the right side wire and the right hand plate is at potential VB.  Yet another way of looking at it is that, inside a metal at equilibrium, the electric field is zero, and so no work is necessary to move a test charge from the end of the wire to the plate.  So, in review, all of the potential drop is across the plates of the capacitor (once equilibrium is reached).

In addition, we know from the definition of capacitance that:
C1 = Q1/V1, C2 = Q2/V2, and Ceq = Qeq/Veq.
Now, we start substituting:
Qeq = Q1 + Q2
CeqVeq = C1V1 + C2V2
But, all the Vs are equal, so we can cancel them out:
Ceq = C1 + C2
Here is our result: the equivalent capacitance should be the sum of the original two capacitances.  Incidently, this is referred to as a parallel arrangement of capacitors.  For more than two such capacitors, just continue to add terms.

Does this make sense?  Try a simple example:
Suppose that we take two identical capacitors Co and connect them as shown above.  The relationship we just derived indicated that the equivalent capacitance is Co + Co = 2Co.  But, we could just as well have connected them +plate to +plate and - plate to - plate without the wires:

in which case, we'd have a single capacitor of spacing d, area 2Ao, and therefor capacitance eo(2Ao)/d = 2Co, as expected.

Let's try an different arrangement:

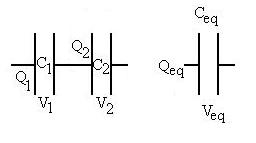
In this case, we can say that Q1 = Q2 = Qeq, since all of the Qeq we put on the capacitors from the left will end up on the left plate of C1, and the Qeq we take off to the right will all come from the right plate of C2, making it possess charge -Qeq.  We expect that the right plate of C1 will then have a charge -Qeq attracted to it by the other plate's positive charge, and that will leave behind charge +Qeq on the left plate of C2.  In addition, we can say that Veq = V1 + V2, again because the electric field is conservative.  Also once again, we know by definition that
C1 = Q1/V1, C2 = Q2/V2, and Ceq = Qeq/Veq.
So start substituting:
Veq = V1 + V2
Qeq/Ceq = Q1/C1 + Q2/C2
But, all the Qs are equal, so cancel them:
1/Ceq = 1/C1 + 1/C2 ,
which is the result for series capacitors.  For additional series capacitors, just continue to add reciprocal terms.
 

What if there is a combination of parallel and series arrangements?  Look for small groupings on one type or the other and reduce them first.  Then combine those simplified equivalent capacitors with it neighbours until only one capacitor is left (or at least until the system is simple enough to determine the answer to your problem).
Try some examples:


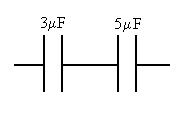
What is the equivalent capacitance of this combination?


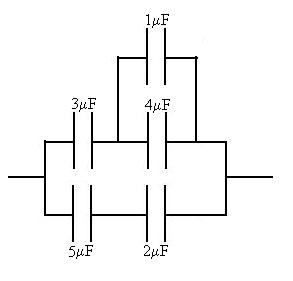
What is the equivalent capacitance of this combination?


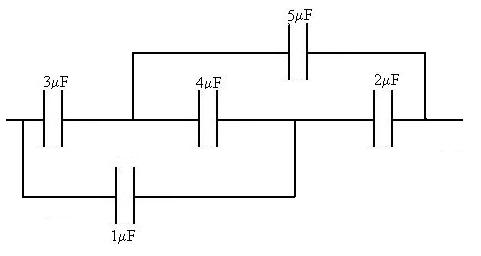
What is the equivalent capacitance of this combination?



Lastly, let's look at a particular example, more as a warning than anything else.  Consider two identical capacitors, C, of which one has charge Qo and potential difference Vo and the other of which is uncharged.  The total energy of this system is then
(UC total )o = Qo2/2C + 0 = Qo2/2C.
After the capacitors are connected, each will have (we won't work this out explicitly here) charge Qo/2, and energy [Qo/2]2/2C = Qo2/8C, and the system will have total energy
(UC total )f = Qo2/8C + Qo2/8C = Qo2/4C.
Note then that a naive application of conservation of energy to solve this problem would not work!  Where did the missing energy go?

In the second case mentioned, will more energy be lost than in the first case?

Additional Examples

Consider a parallel plate capacitor (area A and splate separation d) that is half filled with a dielectric k.  What is the capacitance?

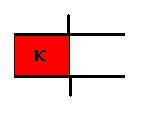
Treat this as a parallel combination.  CTOT = Cdielectric + Cair =  keo(1/2A)/d + eo(1/2A)/d = [1 + k] eoA/2d.

What if the dielectric were arranged the other way?  Let's let the dielectric occupy 3/4 of the volume between the plates.

Two ways to do this (which are ultimately identical).  First, let's slap a thin sheet of metal on the exposed face of the dielelctric.  That makes two capacitors in series, and the total capacitacne should be:
1/CTOT = 1/Cdielectric + 1/Cair = 1/[keoA/(3/4)d] + 1/[eoA/(1/4)d] = 3/4d/keoA + 1/4d/eoA = 3/4d/keoA + 1/4dk/keoA = [3+k]d/ 4keoA
So, CTOT = 4keoA/[3+k]d.
 More directly,
Assume there's a charge +/- Q on each plate.  The field where there is no dielectric is E = s/eo. The field where there is dielectric is E = s/keo.
The potential difference betweet the plates is then
DV = - 03d/4 E.dr - 3d/4d E.dr = - 03d/4 s/keo dr - 3d/4d s/eo dr = - 3ds/4keo - ds/4eo = - 3ds/4keo - dks/4keo = -[3 + k]ds/4keo = -[3 + k]dQ/A4keo =
Drop the minus sign.  Then
C = Q/DV = Q/[[3 + k]dQ/A4keo] = QA4keo/[[3 + k]dQ] = 4keoA/[[3 + k]d] .
Note that if we let k -> 1 (i.e. the capacitor is empty), then we get back our original result of eoA/d.

Two more examples...

Consider a coaxial capacitor filled with two dielectrics.  The inner conductor has radius a, dielectric 1 fills the space from a to b, then dielectric 2 fills the space from b to the outer conductor at c.
We've seen previously that the capacitance of an empty coaxial capacitor is
C = L/[2keln(R2/R1)]
We can consider this to be two series capacitors:
CInner = k1L/[2keln(b/a)] and COuter = k2L/[2keln(c/b)]
1/CTotal = 1/CInner + 1/COuter
    = 2keln(b/a)/k1L + 2keln(c/b)/k2L = [2ke/k1k2L][k2ln(b/a) + k1ln(c/b)]
So, CTOTAL = [k1k2L/2ke]/[k2ln(b/a) + k1ln(c/b)].

Consider a parallel plate capacitor with plate separation d, and plate dimensions W and L.  The space between the plates is filled with two dielectric materials, as shown:

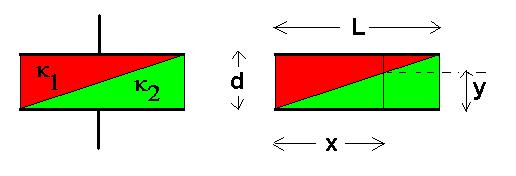
Find CEQ.
Divide the capacitor up into narrow strips of width dx.  Let x be the distance from the left end.  The thicknesses of the two dielectric layers are then y and d-y, where y = (d/L)x.
Each of these mini-capacitors has capacitance
dCUPPER = k1eoWdx/(d-y)   and dCLOWER = k2eoWdx/y.
These two capacitors combine in series:
1/dC = 1/dCUPPER + 1/dCLOWER = (d-y)/k1eoWdx + y/k2eoWdx = k2(d-y)/k1k2eoWdx + k1y/[k1k2eoWdx] = [k2(d-y) + k1y]/k1k2eoWdx
So,
dC = k1k2eoWdx /[k2(d-y) + k1y] = k1k2eoWdx /[k2d + (k1-k2)y] = k1k2eoWdx /[k2d + (k1-k2)(d/L)x] = k1k2eoWdx /d[k2 + (k1-k2)(x/L)]
Now, we want to add up all of these slices that are in parallel:
CTOT = 0L k1k2eoWdx /d[k2 + (k1-k2)(x/L)]
This is amenable to u substitution with u = k2 + (k1-k2)(x/L)  and du = (k1-k2)(dx/L).  This results in
CTOT = [k1k2eoWL /d(k1-k2)] ln [k2 + (k1-k2)(x/L)] 0|L = [k1k2eoWL /d(k1-k2)] ln [k1/k2].
Note that this will work regardless of which dielectric constant is larger.

For fun, you can try to show that if k1 and k2 are equal, this reduces to keoA/d.  HINT: you'll need a Taylor's expansion for the ln term.


Continue to Next Section
Return to Notes Directory

D Baum 2001- 2009