Section 2-8 - Geometric Optics

The Speed of Light

Aristotle concluded that light travels infinitely fast, based on the observation that, when one turns on a lamp, the reflection in a mirror appears immediately.  Some describe this as there being no 'echo,' no delay between the light which took a direct path to our eyes and that which was reflected from the mirror.

The first scientific attempt to measure the speed of light was performed by Galileo, who took a lamp to the top of a hill, while his assistant did the same on a different hill.  Galileo uncovered his lantern, the assistant uncovered his when he saw Galileo's light, and Galileo measured the time from when he uncovered to when he saw his assistant's light.  This experimental technique is still used today and is called a time-of-flight measurement.  Unfortunately, Galileo was only measuring human reaction times.

The next advance was made by Roemer, who observed slight discrepancies in the time between the eclipses of Jupiter's moons.  He concluded that the increase in the period was due to the earth moving in its orbit away from Jupiter, and decreases in the period were due to the earth approaching Jupiter, such that the extra time was that necessary for the light to cross the orbit of the earth, and that the speed of light was therefor not infinite. Huygens used these data and arrived at a value of about 2.3 x10⁸ m/s (the size of the earth's orbit was not well known, then).

In 1849, Fizeau used a toothed wheel, and later Michelson used a rotating mirror apparatus, to determine that the speed of light was about 3x10⁸ m/s.  The idea is that light from a bulb is reflected to a mirror some thirty-five km away when the mirror is in the position shown in the figure.  After completing the round trip, the mirror must have rotated 45^o so that a different face reflects the light to the observer's eye.

If the light is seen for any speed of rotation, then the speed of light would be what?

The Nature of Light

However, by the turn of the ninteenth century, the wave view of the nature of light regained support when Young explained interference and diffraction effects in terms of waves; these effects simply can not be explained in terms of a particle model.  By mid-century, Foucault had shown that Newton's explanation of refraction was based on false assumptions, and Maxwell (1860s) combined Gauss's Law, Ampere's Law, and Faraday's Law to predict the existence of electro-magnetic waves with an expected velocity equal to the known speed of light; the implication seems clear: light is an electromagnetic wave.

In the 1880s, Hertz used a spark-gap to produce electro-magnetic waves of a type we now call radio waves; he demonstrated that such waves exhibit all of the behaviours of light, such as reflection, refraction, polarization, and diffraction, and so he surmised that
1) radio waves are EM waves,
2) light behaves in the same manner as radio waves,
3) therefore, light is an EM wave.
Interestingly, Hertz's experiment, which confirmed the wave nature of light, also exhibited different results when conducted with or without the room lights on, a behaviour which could not be explained with the wave model and which we now call the photo-electric effect.  Einstein was able to explain this effect, but by using a particle-like model for light; these particles are called photons.  It was left to the more mature outlook of the twentieth century to reconcile these two models; we say now that light is neither wave nor particle, but that it exhibits some behaviours of each.

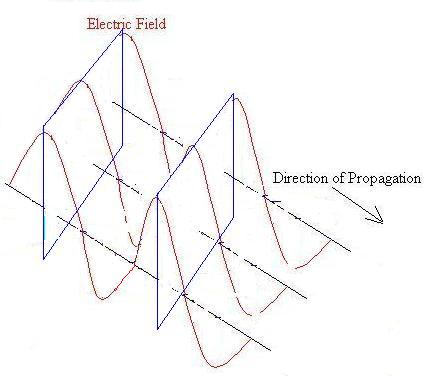
For now, let us consider light to be a wave.

Waves, Wavefronts, and Rays

Reflection, Refraction, and a Surprise

Reflection

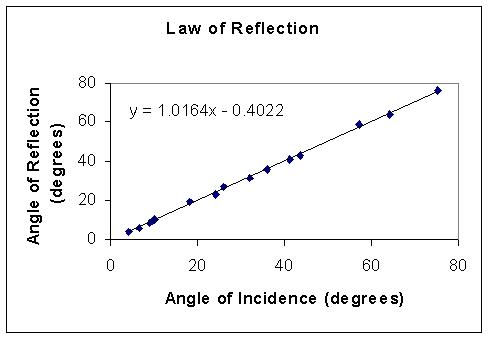
Here are some experimental results comparing the angles of incidence and reflection (2001/2 class):

This property could be explained with either the corpuscular or wave theories of light.  A ball hitting a wall in an elastic collision and without spin will rebound at an angle equal to the incident angle because of conservation of momentum.

The momentum in the x direction will remain unchanged, and the momentum in the y-direction will completely reversed, and so q_r = q_i.
 

For waves, we first need to discuss Huygen's Principle, which states that every point on a wave front can be considered to be a point source for new waves.  Then, we consider a ray (with its corresponding perpendicular wavefront) incident at speed v on a flat surface at angle q₁ as shown.  The edge of the wavefront has just reached Point Aat time t₁:

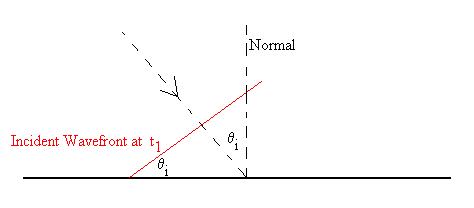
According to Huygen's Principle, Point A will be the source for new waves (Of course, so will many other points on the surface as well, but we'll consider only what happens at Points A & B).  Consider the same wavefront a time Dt later, during which time the wave has moved such that the other edge of the wavefront has arrived at Point B.  The distance that edge has moved in the interval is vDt.  Now according to Huygen's Principle, Point B is a source for new waves.  The wave created at B has not yet had any chance to go anywhere, but the wave from Point A (shown in blue) could be anywhere on a circle of radius vDt centred on Point A.

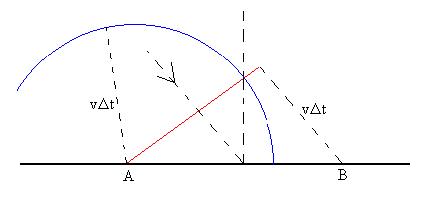
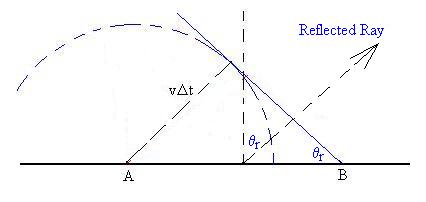
The reflected wavefront has to meet two conditions: first, it must be tangent to the circle we drew around A, since it must be perpendicular to its direction of motion away from A, and it must pass through B.  We can then also generate a ray indicating the direction of the reflected light.  Through some geometry, we knw that the angle at Point B is equal to the angle of reflection, q_r.

Now, we have two right triangles which share a common hypotenuse (between Points A & B) and which each have a side of length vDt.

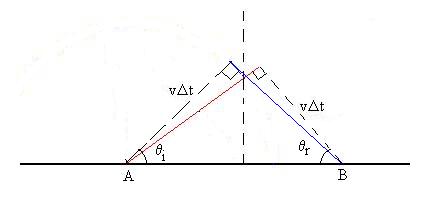
These triangles are therefor congruent, and the angles at Points A and B are equal.  So, too, then are the angles of incident and reflection.

Another point of view is Fermat's Principle of Least Time, which states that light will take the path from one point to another which requires the least time (Strictly speaking, this is a special case of a principle used in mechanics, where the actual statement is that the time is at an extreme.). Consider two points, A and B.  Light travels from Point A to Point B after reflecting off a mirror along the x axis.  Let x represent the spot at which the reflection occurs. 

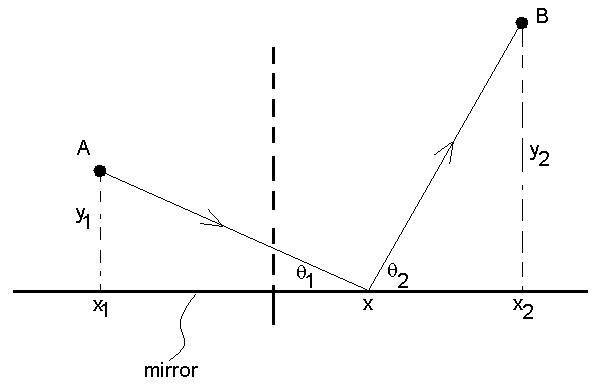
The shortest time in this case also means the shortest distance.  For given reflection point x, the distance travelled by the light will be:
D = [y₁² + (x₁ - x)²]^1/2 + [y₂² + (x₂ - x)²]^1/2

Then set dD/dx = 0

¹/₂[y₁² + (x₁ - x)²]^-1/2[2(x₁ - x)(-1)] + ¹/₂[y₂² + (x₂ - x)²]^-1/2[2(x₂ - x)(-1)] = 0
- [y₁² + (x₁ - x)²]^-1/2(x₁ - x) = [y₂² + (x₂ - x)²]^-1/2(x₂ - x) = 0
cosq₁ = cosq₂
q₁ = q₂

We should of course go back and take the second derivative to show that this corresponds to a minimum.

Refraction

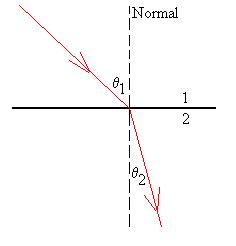
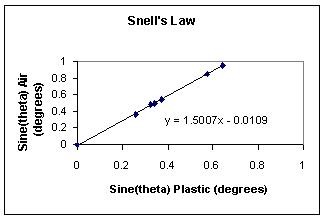
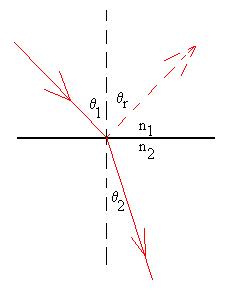
Here are some experimental results comparing the sines of q₁ and q₂ for an air-plexiglas interface (class of 2001/2).  The line's slope represents n_Plexiglas:

We now know that this effect is caused by the fact that light has different speeds in different materials, or in different parts of the same material (see derivation below).  Remember (from above) the wave equation, where we saw that the speed of light (in vacuum) was given by
c = 1/[e_om_o]^1/2.
Think back to the effect of the insertion of a dielectric of constant k into a capacitor:
C_diel = ke_oA/d.
So, if the light wave were to travel through a material with dielectric constant k, we would expect to have to modify our velocity result accordingly:
v = 1/[ke_om_o]^1/2 = c/k^1/2,
that is, the light slows by a factor n = k^1/2, so that
v = c/n;

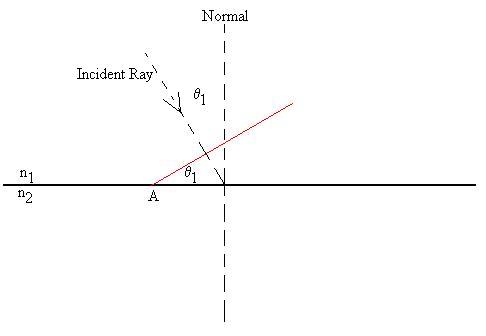
Let's see if we can prove that a change in speed will account for refraction. Consider a wavefront incident on a flat interface at angle q₁ (red line), for which we can consider the wave at Point A to be the source for new waves.

A time Dt later, the waves created at A are somewhere on the dotted curve a distance v₂Dt from A, while the upper end of the wavefront still in material one has traveled a distance v₁Dt to reach the interface at Point B.  To construct the new wavefront in material two, we know that it must be tangent to the dotted curve (since it must be perpendicular to its own direction of motion) and pass through B (blue line).

We observe the two right triangles which share a hypoteneuse (H) between Points A & B

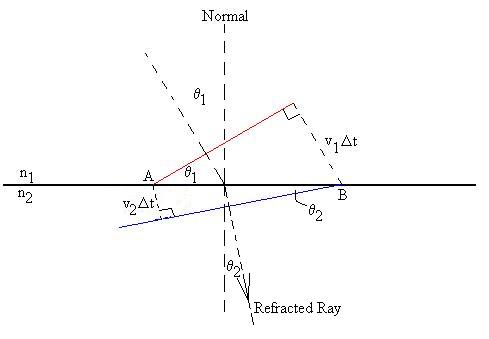
and determine that
H = v₁Dt/sinq₁ = v₂Dt/sinq₂,
(c/n₁)/sinq₁ = (c/n₂)/sinq₂,
n₁sinq₁ = n₂sinq₂.

Newton gave a detailed explanation of how refraction could be accounted for in the corpuscular theory, but we shall not discuss it here, since Foucault showed it to be based on false assumptions.  Realize, though, that it was a well respected theory for over 150 years.

Question:
What would happen if n₁ = n₂?

Then set dT/dx = 0

¹/₂(n₁/c)[y₁² + (x₁ - x)²]^-1/2[2(x₁ - x)(-1)] + ¹/₂(n₂/c)[y₂² + (x₂ - x)²]^-1/2[2(x₂ - x)(-1)] = 0
- n₁[y₁² + (x₁ - x)²]^-1/2(x₁ - x) = n₂[y₂² + (x₂ - x)²]^-1/2(x₂ - x) = 0
n₁ cosq_A = n₂ cosq_B
But, q_A and q₁ are complementary, as are q_B and q₂ , so

Example:
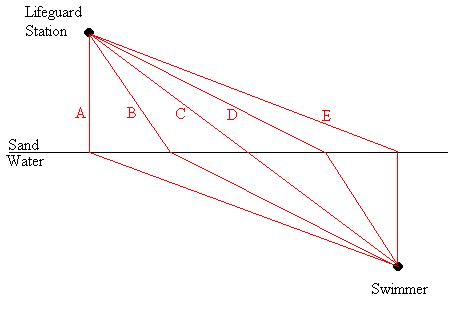
Consider the path a lifeguard should take across the beach and through the water to reach a drowning swimmer as quickly as possible.

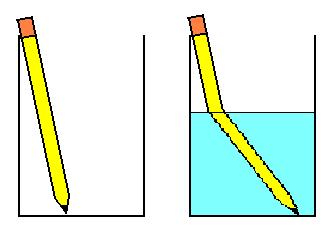
There was a London stage mystery play back in the thirties (of which I'm afraid I have forgotton the title) in which a major plot device was the fact that the stolen jewels had been hidden in a pitcher of water, thus making them invisible.  Would this really work?

The index of refraction is also generally wavelength dependent.  For example, n_glass for light with wavelength 400nm is generally higher than for light of wavelength 700nm.  As a result, these two wavelengths will be refracted along slightly different paths.  If white light comprising all colours is incident on glass, the colours will be spatially separated, forming a spectrum.  Newton coined this expression, because the light so produced appeared 'ghostly.'  Natural examples of such spectra include rainbows and sun-dogs.

Total Internal Reflection

Ray Tracing and Mirrors - Plane, Concave, Convex

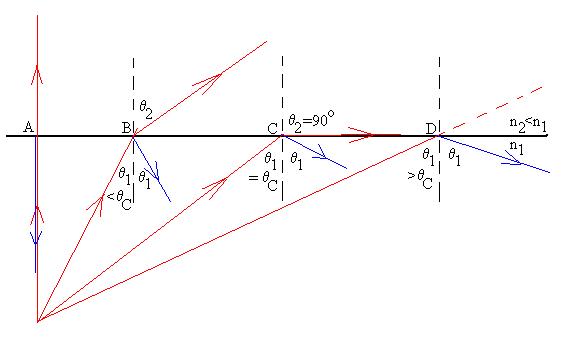
What about mirrors with a curved surface?  We shall restrict ourselves to mirror surfaces which are sections of a sphere, since that will make our derivations a little easier, but you should realize that, in real life, the surfaces could be parabolic or hyperbolic (both common in telescopes) or one of a number of other shapes.

Consider a concave mirror, as shown.  We shall draw in the optical axis as a reference line; it passes through the centre of the mirror, perdendicular to its plane.  If the surface is part of a sphere, there must be a centre to the sphere (CoS), and the distance of this point to the mirror is the radius of curvature of the mirror surface, r.  Now, let's consider a ray which comes into the mirror parallel to the OA, a small distance d away from it (the derivation we're about to do requires small angles).  The ray will hit the mirror surface at an angle q and be reflected at the same angle from the normal.  How do we generate the normal? It will connect that point on the mirror where the reflection takes place to the CoS, i.e., it's a radius of the sphere.  The ray will return to the left and eventually cross the OA at a distance we'll call f from the mirror.

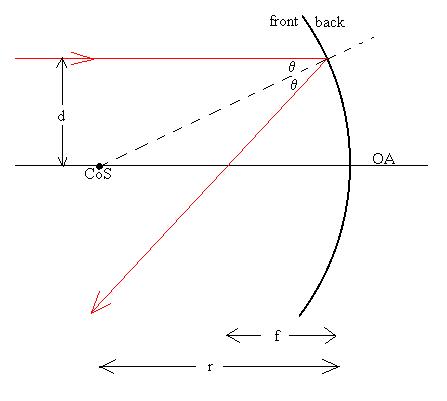
Consider two triangles in this diagram:

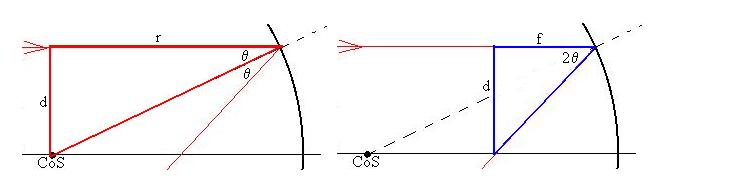
Because of the curvature of the mirror, the distances labelled 'r' and 'f' are not quite r and f, but for small values of d, they will be close.
For the red triangle, we can write that (at least approximately)
d/r = tanq.
For the blue triangle, we can write that (at least approximately)
d/f = tan(2q),
but since the angles are small, we can re-write this as
d/f = 2 tan(q).
Comparison of the two relations tells us that f = r/2, and that this is true regardless of d.  This last bit of information tells us that any ray coming in parallel to the OA will be reflected back through this special point, which we shall now call the focal point.  The distance f is then known as the focal length of the mirror.  Note that this result required a number of approximations, for example, the angles we used must be small, and the tangents of q and 2q are actually a little bigger than we said.
In real life, of course, this is not quite true, and spherical abberation is the result.  Parabolic surfaces do not exhibit such abberation.

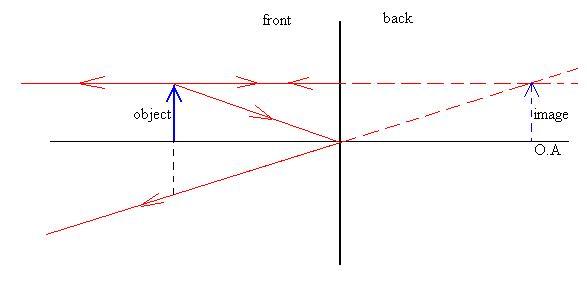
Convex mirrors should also have a focal point, although it is behind the surface of the mirror, and the rays don't actually cross there, they only seem to have crossed there:

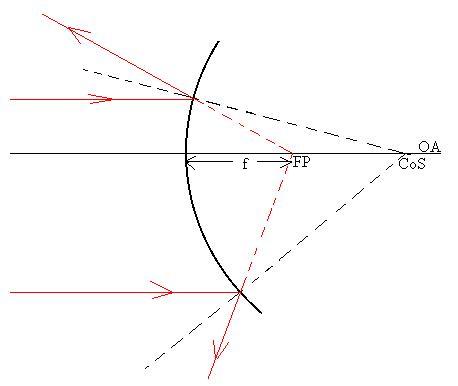
A similar argument can be used to assert once again that f = r/2.
Prove this to yourself.

Let's see if we can use some of this information to predict where an image of an object will form.  We shall use an arrow as our object, because it possesses attributes in which we are interested: location, orientation, size, and as we'll see later, reality or non-reality.  The technique we're about to use is called ray tracing, and it should be done with pencil, paper, and a ruler.
Consider the following situation involving a concave mirror; the mirror is drawn flat to aid in the raytracing process, but keep in mind that the surface is actually curved:

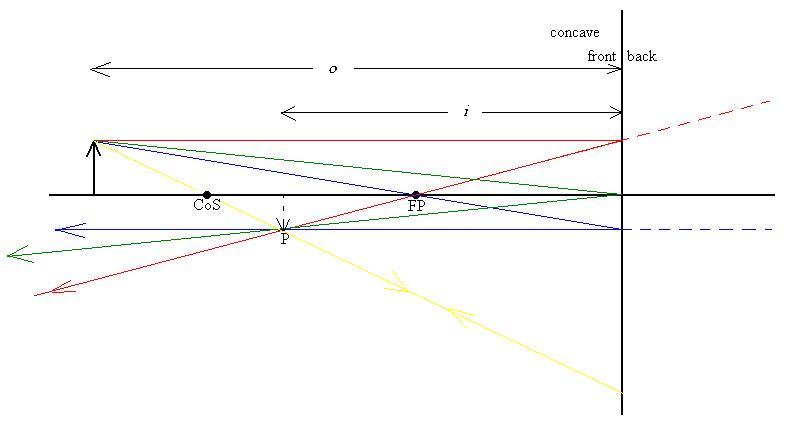
The distance o is called the object distance and it is measured from the mirror surface.  Consider four rays of light which emanate from the head of the arrow:

• The red ray leaves the arrow head, comes in parallel to the OA, then is reflected back through the focal point.
• The blue ray leaves the arrow head, passes through the focal point, hits the mirror, and is then reflected back parallel to the OA; this is essentially the red ray in reverse.

• The green ray leaves the arrow head, hits the mirror at its centre, where the mirror is perpendicular to the OA, and the ray is therefor refleced at the same angle with respect to the OA as it was incident.  We can generate this ray easily, since it will pass under the object at the same distance from the optical axis as the head of the arrow is above it (see figure for the plane mirror, above).
• The yellow ray leaves the head of the arrow, travels along a radius of the spherical surface, hits the mirror normally, and is therefor reflected back along its own path through the CoS.

Here is another diagram using a concave mirror, with the same colour code as above:

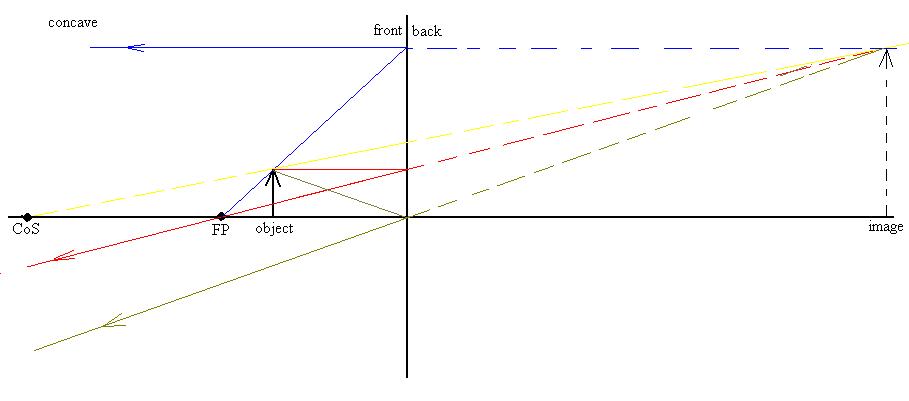
Note that we cannot draw a line from the arrow head through the focal point, then to the mirror, so we need to use a trick: draw a ray (blue) from the focal point which just grazes the arrow head, continue onward toward the mirror, then reflect it back parallel to the OA.  Similarly for the yellow ray, we start at the centre of the sphere, just graze the tip of the object, and continue from there as before.
How would one describe this image?

Here is an example using a convex mirror:

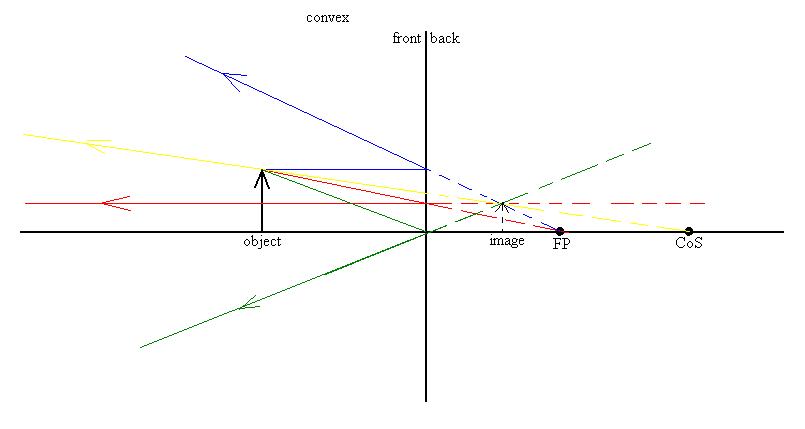
Here, the rays are constructed a little differently, but with a correspondence to the four described above:

• The blue ray leaves the arrow head, comes in parallel to the OA, then is reflected back away from the focal point.
• The red ray leaves the arrow head, head towards the focal point, hits the mirror, and is then reflected back parallel to the OA.
• The green ray leaves the arrow head, hits the mirror at its centre, where the mirror is perpendicular to the OA, and the ray is therefor refleced at the same angle with respect to the OA as it was incident.  We can generate this ray easily, since it will pass under the object at the same distance from the optical axis as the head of the arrow is above it (see figure for the plane mirror, above).
• The yellow ray leaves the head of the arrow, travels towards the centre of the spherical surface, hits the mirror normally, and is therefor reflected back along its own path.

Describe the image.

Ray Tracing and Lenses - Converging and Diverging

Here are the rules we will use for constructing ray diagrams for converging lenses:

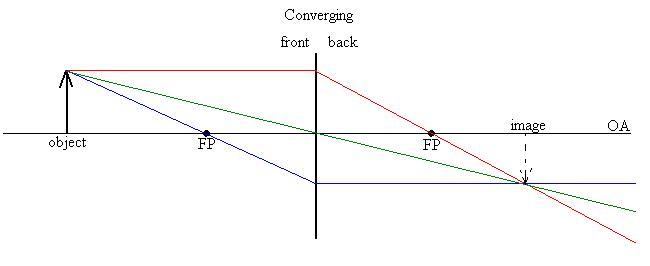
One red ray from the tip of the arrow parallel to the OA, through the lens, and bent through the focal point.
One blue ray from the tip of the arrow, through the other focal point, hit the lens, and come out parallel to the OA.  This is the the rule for the red ray used in reverse.
One green ray from the tip of the arrow, through the centre of the lens undeflected.  This last requires some explanation:

Consider a ray which hits near the centre of the lens at some angle as shown.

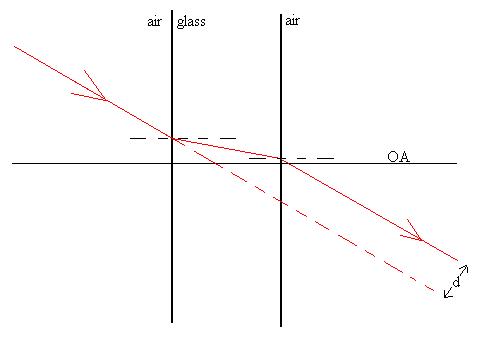
The ray will be refracted at the first surface, which we shall assume is essentially perpendicular to the OA.  It hits the second surface, which is also perpendicular and exits in the same direction as it was initially traveling in.  Why?
n_air sin q_air,left = n_glass sinq_{glass, left}  = n_glass sinq_{glass, right} = n_air sin q_air,right
Note, however, that the ray is offset from its original line of travel, but as the thickness of the lens goes toward zero, the amount of offset (d) also decreases.  So, we conclude that for a thin lens, the ray through the centre is undeflected.
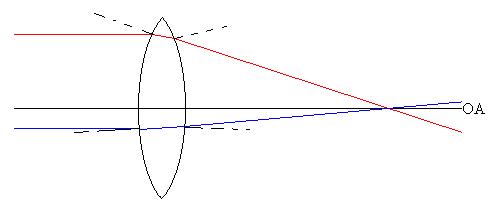
Describe the image produced above.

A diverging lens spreads out light coming in parallel to the OA, so that it seems to have come from the focal point:

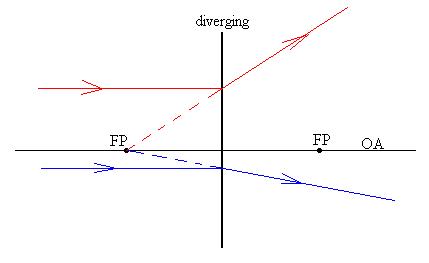
Here is an example of ray tracing for a diverging lens:

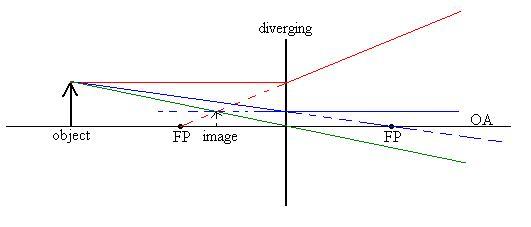
One red ray from the tip of the arrow parallel to the OA, through the lens and bent away from the focal point.
One blue ray from the tip of the arrow, towards the other focal point, hit the lens, and come out parallel to the OA.
One green ray from the tip of the arrow, through the centre of the lens undeflected.
Describe this image:

Let's try another converging lens, where the object is inside the focal length:

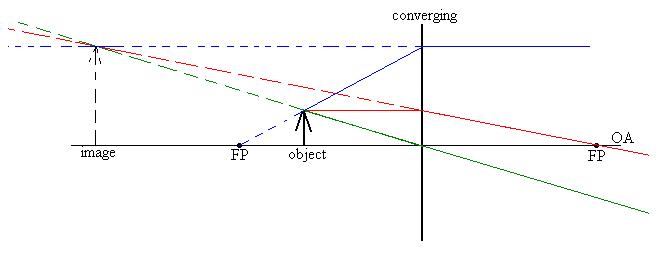
One red ray from the tip of the arrow parallel to the OA, through the lens and through the right hand focal point.
Blue ray: here, we had to use our trick again, starting from the left hand focal point, just grazing the tip of the arrow, hit the lens, and come out parallel to the OA.
One green ray from the tip of the arrow, through the centre of the lens undeflected.
Describe this image:

Question:
Occasionally, students will ask, 'Which ray (of the many) from the object will reach the image first?'

The Thin Lens Equation

Let's briefly consider the meaning of having a 'virtual object.'  Suppose that there are two (or more) lenses or mirrors through which light must pass.  Where will the final image form?  What we do is consider each optical element separately.  Find the image produced of the actual object by the first optical element, then use that as the object of the second element.  In some cases the image of the first element will form behind the second element, and so we consider it to be a virtual object.

Defects of the Eye

The retina has two basic types of photoreceptors:

Cones, which are concentrated near the center of the retina (the fovea), appear to be able to distinguish among three basic colors (red, green, and blue, each with some overlap into neighboring parts of the spectrum), but which are not sensitive to low light levels. The figure is very qualitative and the exact shapes of the curves vary from person to person.

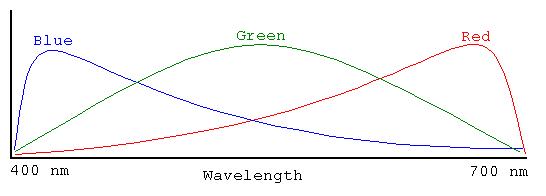
It is thought that light of any single given wavelength will excite all three types of photo-receptors in a unique combination; however, the correct combination of several wavelengths can produce the same sensation as would a single wavelength not actually present!  For example, consider the eye's response to a single wavelength of yellow (589 nm), which excites equal amounts of green and red, plus a little blue, then consider a combination of a red wavelength (670 nm) and a green wavelength (535 nm) which excites the eye receptors in the same proportions; that combination will be perceived as yellow, even though no yellow light is actually present.

A second example: Light of just two wavelengths, 480 nm and 580 nm, can stimulate the same response as a complete spectrum of white light.

In fact, this is how color televisions work, by using mixtures of three basic or primary colors to evoke in the human eye the sensation of colors which are not actually present.
Lastly, since the actual response curves can vary from person to person, it is entirely possible that one person's orange could look very different from another person's orange.

Rods, which are very sensitive to low levels of light, are more evenly distributed over the retina, but do not distinguish between different colours of light.  The photosensitive chemical in the rods is rhodopsin.

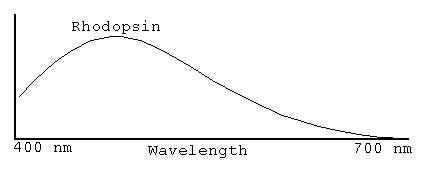
In low light levels, humans lose their color perception (Try it! Go out before dawn, and everything is in black and white!), since only the rods are receiving enough light to trigger signals to the brain; at higher light levels, the rods shut off and the cones take over.
Normally, in going from a bright room to a dark room, there is a time delay until the cones shut off and the rods turn back on.  The poor response of rhodopsin in the red part of the spectrum allows humans to preserve their night vision by using only red light while still indoors.  Since the rods' response is not saturated by the bright red indoor light, the rods can begin seeing in the dark almost immediately.

It is thought that photo-chemical reactions in these cells initiate signals sent along nerves to the brain for processing.  While most nerve connections for each side of the body are sent to the opposite side of the brain, vision signals from each eye are sent to both sides of the brain.

Color Blindness

Myopia

Hyperopia

Presbyopia

Astigmatism

Question:
Recall the book or films of The Lord of the Flies by William Golding.  In that story, Piggy's glasses were coveted by both tribes of boys as a tool to start fires.  What flaw is there in this plot device?