Section 1- 3 - Motion in Two Dimensions
Graphical Addition of Vectors
Decomposition of Vectors
Motion in Two Dimensions
Projectile Motion in Two
Dimensions
Shape of a Projectile's Path
The Range Equation
Relative Velocity
Correlation
to
your Textbook
Graphical Addition of Vectors
We talked in the last section about vectors in one dimension, but
wimped
out a bit by indicating the direction with the sign of the
quantity.
Let's move on to two dimensions.
A scalar is a quantity with only magnitude (e.g.,
temperature).
A vector is a quantity which has both magnitude and direction
(e.g., wind velocity).
Are there other types of quantities? Yes, the next one up is
called a tensor, followed by super tensors, super-super
tensors, et c.
The names of vectors are written in bold type in print, or with an
arrow when handwritten: A or  .
The magnitude of a vector is denoted by dropping the bold type, or by
enclosing
the symbol with vertical lines: A or |A|.
.
The magnitude of a vector is denoted by dropping the bold type, or by
enclosing
the symbol with vertical lines: A or |A|.
For now, it might be useful to visualize vectors specifically to
represent
displacements, while realizing that they may also represent much more
abstract
quantities. So, in that sense, the vector A tells us to
travel
so far in such-and-such a direction. An example might be 5 km at
qA=37o,
remembering that the angles are customarily measured CCW from the
x-axis.
We can visualize adding vectors again in terms of displacements: A
+ B says that we should start at our origin and travel A m in a
direction given by qA, then from
that intermediate destination, travel B m in the direction given by qB.
Conceptually, this is known as the tip-to-tail method of addition:
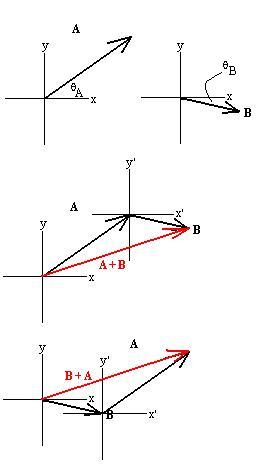
We can move the vectors around at our convenience to add them as shown,
since a vector is defined only by its magnitude and direction; so long
as those are kept the same, we can slide the vector around the page as
much as we want.
We realize that addition is commutative (see figure above) and
associative
(not shown). The vector A + B can be given its
own
name (C?) so that we can write that
C = A + B = B + A.
C is called the resultant of the addition of A and
B. Here is an equivalent alternate method, called the parallelogram
method of addition:
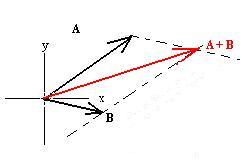
Place the vectors tail to tail, then construct lines parallel to each
through the tip of the other. The diagonal is then A + B.
You
can see how these methods are identical: the lower triangle
corresponds
to the one in the B + A figure above, while the upper
one
corresponds to the A + B figure above.
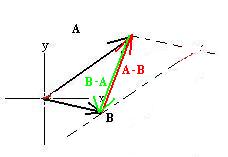
Subtraction of vectors is not obvious, but we can take a leaf from
the
algebraists' notebook:
A - B = A + (-B),
where (-B) is a vector with the same magnitude as B,
but directly oppositely.
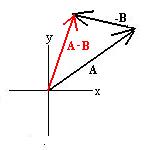
Comparison to the parallelogram method reveals that A - B
is the other diagonal of the parallelogram (as is B - A
pointing
in the opposite direction):
To add vectors graphically, one would take paper, ruler and protractor,
choose a scale, and draw arrows to represent the vectors such that the
length of each is proportional to the magnitude of the corresponding
vector.
To find the resultant, measure the length of the resultant with the
ruler
and back convert to find the magnitude, and use the protractor to find
the direction.
Decomposition of Vectors
Now that we can add vectors, we can also see that any given vector
(shown
in black) can be written as the sum of two (or more) other vectors:

If that's true, we might as well choose two vectors which will be
convenient
for us. If we make the two vectors perpendicular, we might be
able
to use trig relationships to suss out some info.
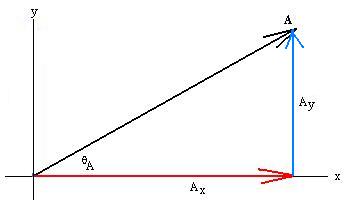
Ax is called the x-component of A and Ay
is the y-component of A, that is, how much the vector
points
in each direction. Ax and Ay are actually
scalars,
although they can be positive or negative or zero. We convey the
directional information through the use of the unit vectors i
and
j. Unit vectors have length one and are dimensionless (that
information
is carried in the components). So, we can write that
A = Axi + Ayj.
From trig, we see that Ax = AcosqA
and that Ay = A sinqA.
Note
that if we measure qA CCW
from
the x axis, that the signs of the trig functions correctly give the
signs
of the components. Here is an example:
Let A be 15 m at qA= 120o,
which
is in the second quadrant. We find that
Ax = A cos qA =
(15m)*cos(120o)
= - 7.5 m Ay
= A sin qA = (15m)*sin(120o)
=
13 m
and the signs of these components match what we know about the
direction
of A.
Now, we have an alternate manner of adding vectors using the
components.
Let C = A + B:
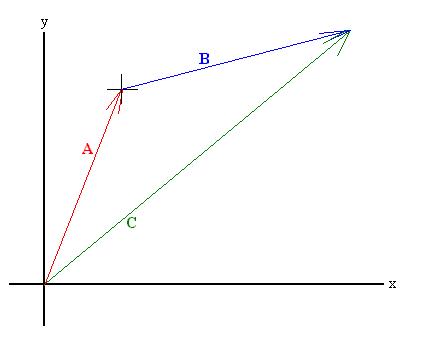
Let's draw in the components of both A and B, as well as of C:

It should be clear that Cx = Ax + Bx
and that Cy = Ay + By. We might
say that the each component of the sum of two vectors is the sum of the
corresponding components of the two vectors. Subtraction of
vectors
works the same way.
Converting C back into a magnitude and direction is easy:
Use
the Pythagorean theorem to find |C|:
C = [Cx2 + Cy2]1/2
and qC = arctan[Cy/Cx].
Be
sure to watch the quadrant!
Motion in Two Dimensions
We need a new way of keeping track of the motion of a particle.
Let's
define the position vector r as
r = xi + yj.
The displacement is then
Dr = rf - ri
= (xf i + yf j) - (xii
+
yij) = (xf - xi)i
+ (yf - yi)j = Dxi+
Dyj,
so that the displacement is the vector sum of the individual
displacements
in the x and y directions (no surprise there).
The average velocity is vave = Dr/Dt
= [Dxi +
Dyj]/Dt = [Dx/Dt]
i+
[Dy/Dt]
j] = (vx)avei
+
(vy)avej.
The instantaneous velocity v is defined as before as lim Dt->0Dr/Dt.
The average acceleration is aave = Dv/Dt
= [Dvx i +
Dvy j]/Dt = [Dvx
/Dt]
i+
[Dvy
/Dt]
j] = (ax)avei
+
(ay)avej.
The instantaneous velocity a is defined as before as lim Dt->0Dv/Dt.
Consider a ball whirled around on the end of a string at constant
speed.
Is the velocity of the ball constant? Is its acceleration?
Projectile Motion in Two
Dimensions
We shall make three assumptions here:
- Once an object is launched, its acceleration is a constant ag
downward.
- Air resistance is negligible.
- The motions in the x and y directions are independent.
This last factoid we confirmed by observing a demonstration.
First,
two balls were released from rest at the same time and allowed to fall
toward the table; they arrived at the same time. Then, one ball
was
dropped while the other was launched horizontally from the same height
at the same time; once again, they arrived at the same instant.
We
concluded that the vertical motion was independent of any horizontal
motion
the objects may have possessed. (In fact, there are some
situations
where this is not true, for example when the air flow around an object
is turbulent, but we'll ignore them.)
So, we may write our kinematic equations separately for the two
directions:
vfx = vix + ax
t
x = xi + vix t + 1/2ax
t2
vfx2 = vix2 + 2ax
(x f -
xi)
vx ave = [vfx + vix]/2 |
vfy = viy + ay
t
y = yi + viy t + 1/2ay
t2
vfy2 = viy2 + 2ay
(yf -
yi)
vy ave = [vfy + viy]/2 |
The only quantity common to the two systems is the time, t.
Example:
A ball is rolled horizontally off a table 1.5 m in height at 5
m/s.
How far from the base of the table will the ball strike the floor?
Draw a figure to help visualize the situation, including a system of
axes with an origin (here, at the edge of the table, with y positive
upward
and x positive to the right):

Write down all we know:
Set yi = xi = 0. Then, yf =
-1.5
(the ball moved downward) and xf is the distance from
the
base we're looking for.
vix = vi cosqi
= vi = 5 m/s viy
= vi
sinqi = 0
ax = 0 ay = -ag = -10
m/s2
Now, choose which relationships to use; since we need the time to link
the two motions, and we also need to know something about the
displacements,
choose
x = xi + vix t + 1/2ax
t2
and
y = yi + viy t + 1/2ay
t2.
Simplify the y equation and substitute in the values:
-1.5 = 0 + 0* t + 1/2(-10)t2.
t2 = (-1.5)*2/(-10) = 0.3
t = +/- 0.55 seconds - We want an answer which is in the future, so
t
= 0.55 s.
(Why two answers? Once again it's a question of the equations
not being very smart. All they know is that at t = 0, the ball is
at height y = 0 with a horizontal velocity of 5 m/s. They assume
that the ball got there by rising up to that point, i.e., they
assume
that the y-acceleration was -10 m/s2 all along.)
Substitute this result back into x equation:
x = xi + vix t + 1/2ax
t2
x = 0 + 5 *0.55 + 1/2*0*t2
x = 2.7 m
Here is another example:
Take the same ball as above and launch it at at 5 m/s at a 30o
angle above the horizontal. How far from the foot of the table
will
it land? Use the same origin and co-ordinate system as above.
Write down all we know:
Set yi = xi = 0. Then, yf =
-1.5
(the ball moved downward) and xf is the distance from
the
base we're looking for.
vix = vi cosqi
= (5 m/s)*cos30o = 4.3 m/s viy
= vi sinqi
= (5
m/s)*sin30o
= 2.5 m/s
ax = 0 ay = -ag = -10
m/s2
As before,
x = xi + vix t + 1/2ax
t2
and
y = yi + viy t + 1/2ay
t2.
Simplify the y equation and substitute in the values:
-1.5 = 0 + 2.5* t + 1/2(-10)t2,
or
5t2 - 2.5t - 1.5 = 0
Here, we have a quadratic equation, the solutions of which are t =
-0.35 and +0.85. We want an answer which is in the future, so t
=
0.85 s.
Substitute this result back into x equation:
x = xi + vix t + 1/2ax
t2
x = 0 + 4.3*0.85 + 1/2*0*t2
x = 3.7 m
Shape of a Projectile's Path
Let's try to determine the type of path a projectile will take through
space near the surface of the earth. Start once again with the
kinematic
equations:
x = xi + vix t + 1/2ax
t2
y = yi + viy t + 1/2ay
t2
Let viy = vi sinqi
and vix = vi cosqi.
Also, ax = 0 and ay = ag.
Lastly, since our choice of origin is arbitrary, let's set xi
= yi = 0 for simplicity.
So,
x = vi cosqi t
y = vi sinqi
t + 1/2ag
t2
Re-arranging the first equation gives us:
t = x / vi cosqi.
Substitute this into the y-equation:
y = vi sinqio [x
/vi
cosqi] + 1/2ag
[x
/vi cosqi]2
which simplifies to :
y = tanqi x + 1/2ag
[x
/vi cosqi]2
For any given situation, qi,
vi, and ag are constants, so this
relationship
has
the form
y(x) = Ax2 + Bx
and the path is parabolic.
The Range Equation
Let's discuss a special case of projectile motion which is of
historical
interest. In the 17th and 18th century,
being
a physicist usually meant being an artillery officer. Consider a
flat plain (which is also a plane) on which are located a battery and a
target. Given an initial projection angle qo
(elevation) and speed vo (muzzle velocity, for
guns or cannon), how far will the projectile land from the gun (range,
R)?
We'll assume, since the plane is horizontal and flat, that yo
= yf = 0.
Assume that up is positive y and that the direction from cannon to
target is positive x.
Also, let's say that xi = 0, xf = R, ax
=
0 and ay = ag.
And, let viy = vo sinqo
and vix = vo cosqo.
Then,
xf = xi + vix t
+ 1/2ax
t2
y = yi + viy t + 1/2ay
t2
so that, after substitution,
R = vo cosqo t
0 = vo sinqo t + 1/2ag
t2
Solving the second equation for t (times at which the projectile is
at ground level) results in
t = 0
and
t = [2vosinqo]/(-ag)
Note that ag is presumably a negative number, so the
denominator
above is positive.
R = vo cosqo [2vosinqo]/(-ag)=
vo2 [2sinqocosqo]/(-ag)
=
vo2 [sin(2qo)]/(-ag)
where we've made use of one of the trig identities. Our result,
the range equation, is then
R = vo2 sin(2qo)/|ag|,
where we've fixed any potential sign problems by taking the absolute
value of ag.
Let's consider a couple of questions:
First, what angle(s) give(s) the maximum range for a given muzzle
velocity?
The sine function is a maximum (1) when the angle (2qo)
is
90o, so the elevation angle should be half that, or 45o,
to
attain maximum range.
Second, for a given range and muzzle velocity, at what angle(s) should
a projectile be launched? Re-arranging the range equation results
in:
sin(2qo) = R |ag|/vo2
.
As we saw above, if R |ag|/vo2
= 1, then only 45o will do the job. But if R |ag|/vo2
< 1, then there are two angles which will work:
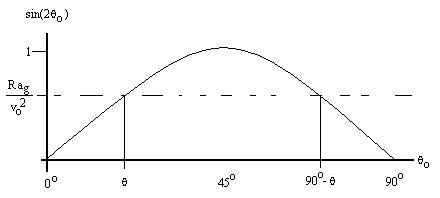
What's more, those two angles will be complementary, since the
curve shown is symmetric.
Example: At what angles can a projectile be launched at 300
m/s
in order to hit a target on the same level which is 5 km away?
So, what's the difference between these two paths? At a low
angle,
the projectile is not in the air long, but it has a high x-component of
velocity, while at a high angle, the projectile spends a lot of time in
the air, but has a correspondingly lower x-component of velocity.
These two effects combine to give the same final x displacement as for
the low angle case. The first is useful in tank warfare, where it
is important to hit the other guy before he gets off a shot at you,
while
the second is good if there are fortifications around your target.
What if R |ag|/vo2
>1? Then there is no angle that can get the projectile to the
target;
it will fall short.
Just as an aside, how long are these times? We saw above that
t = [2vosinqo]/|ag|
and so the other time is
t' = [2vosin(90o-qo)]/|ag|
t' = [2vocosqo]/|ag|
What can we say about the maximum altitude hmax attained
by the projectile?
vy2 = viy2 + 2ay
(y - yi)
Let yi = 0, viy = vosinqo,
ay = ag, and let up be positive.
At the highest point in the trajectory, vy = 0 and y = hmax,
so,
0 = [vosinqo]2
+ 2ag (hmax)
hmax = [vosinqo]2/(-2ag)
= [vosinqo]2/2|ag|
Relative Velocity
On occasion, it is useful to consider the motion of an object with
respect
to an origin/co-ordinate system which is itself in motion to some third
reference frame. The simple example given in class was that of
the
moving sidewalk-type 'people mover' seen at most large airports.
These conveyances allow the weary to ride from one end of the concourse
to the other, while also providing those in a rush a little extra speed
as they run down the walkway. For example, consider such a
walkway
(W) which moves with a speed of +2 m/s with respect to the ground (G):
vW,G = +2 m/s (once again, we'll use the sign of the number
to indicate the direction of the vector quantity).
The subscript notation vA,B gives the velocity of A with
respect to B.
Now, think of a person (P) walking in the same direction at 1 m/s along
the walkway: vP,W = +1 m/s.
It's easy to see that the person's velocity with respect to the ground
is +3 m/s, since
vP,G = vP,W + vW,G.
What is the person decided to walk backward on the walkway, such that
vP,W = -1 m/s? Then, vP,G would be only +1
m/s; the person would still be going in the same direction as before,
although
more slowly. If he walked at -2 m/s with respect to the walkway,
he'd actually be standing still with respect to the ground, and
incidently
greatly annoying his fellow travelers.
Question: Suppose that this traveler walks the correct way on
the 'people mover' at a speed of 1 m/s, while his twin brother walks at
2 m/s the correct way on the return walkway. What is the relative
speed between the brothers?
Now, let's examine the relationship above more carefully:
vP,G = vP,W + vW,G.
One of the hardest aspects of relative velocity is to determine which
two quantities get added to obtain the third. Notice, though,
that
in the example, the lettre 'P' representing the person occupies the
first
subscript position in both of the terms it appears in, while the 'G'
occupies
the second position in both terms; only the 'W' changes position.
A quick way to remember is to add the two terms from which one
subscript
changes position.
Since we can add velocity vectors independently in the x, y, and z
directions,
we can rewrite the relationship above more generally as
vA,C = vA,B + vB,C.
Here's another example:
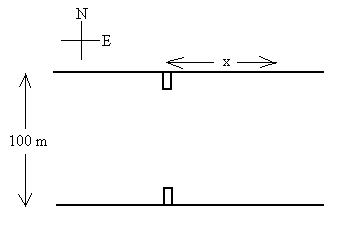
Consider a boatman who wishes to cross a river (100 metres wide) from
one dock north to another exactly opposite. His boat will make 20
m/s in calm water. The velocity of the water is 8 m/s
eastward.
He aims his boat exactly northward and sets off. How far
downstream
(x) will he actually land, in what compass direction did he actually
travel,
and how long will it take him to get there?
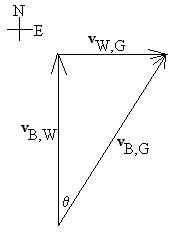
We write the relative velocity
relationship
as
vB,G = vB,W + vW,G,
where
B = 'boat,' W = 'water,' and 'G = 'ground.'
There are a number of ways to solve this; the shortest may be to
realize
that, if the velocity components are all constant, a displacement
component
diagram can be constructed,
DrB,G = DrB,W
+DrW,G,
where each term is parallel to the corresponding velocity term.
The two triangles so formed are then similar, and so there is a
proportionality
of the lengths of the sides:
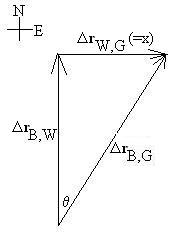
20/8 = 100/x; x = 40m (downstream).
The direction traveled can be found using the tangent of the angle
q:
tanq = 8/20; q
= 21.8o.
For the time, we consider that the motion northward (in this case)
is independent of the motion eastward; it wouild take 5 seconds to
cover
100 metres at 20 m/s.
Now, suppose that, having learned his lesson, he tries again to
cross
directly to the other side. In what direction should he aim his
boat
(relative to north) to arrive exactly at the other dock, and how long
will
it take him??
The common error here is simply to flip the triangle over. But
what should be done is to deform the triangle by sliding vW,G
over
until the sum, vB,G, is pointing due north:
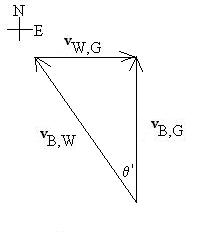
Before, the two short sides of the right triangle were vB,W
and vW,G, but now those vectors are the hypotenuse
and a short side, respectively. So,
q ' = arcsin(8/20) and |vB,G
| = 20cosq '.
Finish the calculations yourself.
Mastery Question
Suppose that a man tosses a ball vertically while riding a train
moving
at constant velocity vT. What shape trajectory will
the
man see the ball take? What shape trajectory will someone
standing
by the side of the track see the ball take?
Now, suppose that the train accelerates forward (aT) and
the ball is launched as before when the train has velocity vT.
What
path will the observer in the train see the ball take? What
path will the stationary observer see?
Click here for solution.
Try this Applet: http://users.erols.com/renau/velocity_composition.html
Return to Notes Index
Continue to Next Section of Notes
D Baum 2000, 2001, 2002













