Section 1-6 - Work & Energy
Work & Energy
Conservative and
non-Conservative
Forces
Potential Energy
Conservation of Mechanical
Energy
& Conservation of Total Energy
Springs
Power
Correleation
to
your
Textbook
Work & Energy
We started by observing an object at rest on the table, then the
same
object
in motion. We agreed that there is some quality the object
possesses
in the later case which it lacks in the former. Let's call
that
quality
energy.
How was that quality transferred into the object? A force
was
applied, but the force must have acted through a
displacement.
Let
us call the transfer of energy into (or out of) an object the work
done
on the object. The bigger the force, the more energy is
transferred,
and the greater the displacement over which the force acted, the
more
energy
is transferred. What's more, there is an effect due to the
relative
orientation of the force with the displacement:
If F and Dx are in the
same
direction, energy is transferred into the object and we
say
that
positive work was done.
If F and Dx are in the
opposite
directions, energy is transferred out of the
object and
we
say that negative work was done.
If F and Dx are
perpendicular,
no
energy is transferred into the object and we say that no work was
done.
How can we write this in a more mathematical way? Let the
work
W be defined as:
W = F (Dx) cosqF,Dx,
that is, as the magnitude of the force times the magnitude of the
displacement,
times the cosine of the angle between those two
vectors.
So,
if F and Dx are
parallel,
qF,Dx=
0o and W = FDx (positive).
if F and Dx are anti-parallel,
qF,Dx
= 180o and W = - FDx
(negative).
if F and Dx are
perpendicular,
qF,Dx
= 90o and there is no work done.
The guess of the cosine function is not quite as arbitrary as it
seems.
Consider a force applied at some random angle as shown here.
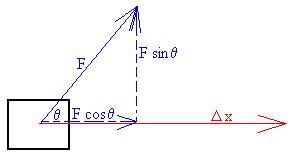
We can always decompose the force vector into a component
perpendicular
to the displacement (which will do no work) and one parallel (or
anti-parallel)
to the displacement which will perform work
W = (Fcosq) Dx,
as before. This leads us to an alternate way of writing the
definition
of work:
W = F|| Dx.
Indeed, we could also look at the work as the whole force times
the
component of the displacemnt in the direction of the force:
W = F Dx ||.
| It might be useful to introduce vector multiplicaton
at this
point. There are several types of multiplication, of
which we
will
discuss two.
We define the scalar product (also called the inner
product
or the dot product) of two vectors A and
B to
be:
A.B = |A| |B| cosqA,B,
= ABcosqA,B,
that is, the magnitude of A times the magnitude of B
times the cosine
of the angle between them. One interpretation of
this definition
is that we are multiplying the magnitude of A
vector by the
component
of B that lies in the direction of A:
A.B = AB|| = ABcosqA,B.
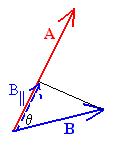
The work is an example. We can write that W = F.Dx.
Another type of vector multiplication is the vector
product or
the cross
product: AxB. We define the
magnitude of the cross
product to be
|AxB| = |A| |B| sinqA,B,
=
AB sinqA,B.
The direction of AxB is perpendicular to
the plane that
contains A and B and can be obtained by
using the right-hand-rule
(RHR). Point the index finger of the right hand in
the direction
of A and the middle finger in the direction of B;
the
right
thumb then points in the direction of the cross
product. One
interpretation
of the cross product's magnitude is that it is the area
of the
parallelogram
formed by the vectors A and B when they
are placed tail
to
tail:

The base of the parallelogram is A and the height is
Bsinq,
making the area A(Bsinq).
What is the
direction of AxB in this example?
We'll discuss
quantities that
can
be written as cross products later. |
What if the force applied were not constant (or, a variable
force)?
Clearly,
more work would be done in some displacement intervals than in
others.
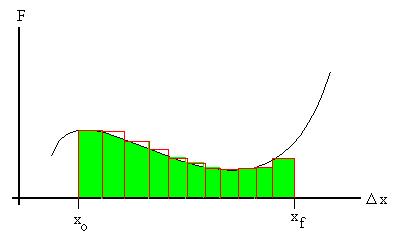
We need to break the overall displacement down into very small
displacements
Dxi,
over which we can consider the force to be relatively constant at
value
FDxi; we then find the work
done
over that interval to be WDxi
= FDxi Dxi
.
Then the work done by the force is
WF = SDxi WDxi
=
SDxi
FDxi
Dxi
This value approaches the area under the force-displacement curve
as
the widths of the Dxi's go
toward
zero.
What if the curve were to go below the axis? Then the work
would
be negative. What if the Dx
values
were
negative? That would also switch the sign of the work.
Let's stop for a second. We've defined the work, but we can
define
anything we please to be whatever we please; what's the
point?
The
definition is meaningful only if it is useful. Let's think
back
to
the beginning of this discussion. We talked about the work
on an
object as a transfer of energy, so that we should be able to say
that
the
work is the change in the amount of this energy stuff that
the
object
possesses, i.e., W = DE.
Keep
this
in mind as we do a little derivation:
First, let's simplify by restricitng ourselves to a one
dimensional
world; the directions of the forces and displacements will be
carried
by
the signs of those quantities (like we did in the kinematic
section),
such
that a negative force and a negative displacement, when
multiplied,
will
result in a positive work, as before (check the other combinations
yourself).
Consider the total work done on an object, which is the
sum of
the
individual works done by each force:
WTOT = Si Wi
=
Si
[Fi
Dx]
= [ Si
Fi
] Dx.
Now, let's invoke Newton's Second Law, Si
Fi
= ma, and substitute:
WTOT = [ma] Dx = m[a Dx].
Note that this will only work if we are finding the total work
done
on the object. Why?
Consider one of our kinematic
equations:
vf2 = vo2
+ 2a Dx.
Looks like we could do a
substitution:
WTOT = m[a Dx] = m[vf2
- vo2]/2 = 1/2mvf2
- 1/2mvo2.
Well, this is interesting. We've found a quantity for which
the
work done on an object is the change in the amount of that quantity
the
object possesses. That sounds a lot like the energy.
Let's
tentatively define the energy E as 1/2mv2.
Let's be a bit more specific; when we spoke of the quality the
demonstration
object possessed as the energy, it possessed said quality due to its
motion,
so we shall define the kinetic energy 1/2mv2
as energy by virtue of motion.
WTOT = DKE.
This last relationship is called
the work-energy theorem. It is the second 'picture'
of
the
three we shall use to solve problems, the first being forces and
accelerations.
| Net force |
causes |
change in velocity (acceleration) |
| Net work |
causes |
change in kinetic energy |
| ? |
causes |
change in ? |
Note that it is nothing more
than
Newton's Second Law, combined with one of the kinematic
equations, plus
a definition. Why bother? We will find that this
picture
will
be on occasion more convenient to use than forces and
accelerations,
especially
in cases where we don't need to know the time a trip takes, or
when the
acceleration is not constant (see Note 1
below).
Note also that work is a
scalar.
Since the kinetic energy depends on the speed of an object, and
not the
direction of the object's motion, it is a scalar; the work is
the
change
in the KE, so it too is a scalar. Although we did this
derivation
for one dimension, it can be done quite easily for three with
the same
result (see Note 2 below). A
combination
of
these arguments let's us assert that the result is valid even
for
variable
forces in three dimensions.
Here are some examples:
Let's throw a ball upward with an initial speed of 12 m/s.
How high does it rise (h)?
The only force acting on the ball is its weight, gm,
downward. The displacement is h upward, so our angle is 180o.
The work done is therefor
Wg = (gm)(h)(cos 180o) = -gmh.
The ball stops at its highest altitude, so vf = 0.
So,
-gmh = 1/2 m vf2 - 1/2
m vi2
-gmh = - 1/2
m vi2
gh = 1/2 vi2
gh = 1/2 vi2
h = vi2/2g = 122/(2*10) = 7.2 m.
Consider a block of mass m = 5
kg
at the top of a frictionless ramp L = 2 metres long, which is
inclined
at q
= 37o to the horizontal.
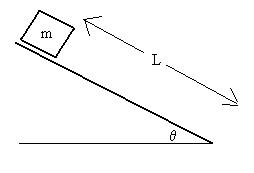
If the mass starts from rest at
the top, how quickly will it be moving when it reaches the
bottom?
Draw a free-body diagram:
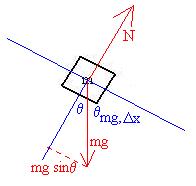
WN = 0, since the force is perpendicular to the
displacement
Wg = mg L cosqmg,Dx
WN + Wg =
1/2mvf2
-
1/2mvo2
mg L cosqmg,Dx
=
1/2mvf2
vf2 =
2g L cosqmg,Dx
vf =
[2g L cosqmg,Dx
]1/2
= [2*10*2*cos53o]1/2 = 4.9 m/s.
Now, let's suppose that the block started out with an initial
velocity
of 6 m/s down the plane. Make a guess what the speed will be
at
the
bottom:
Let's work it out:
WN + Wg =
1/2mvf2
-
1/2mvo2
mg L cosqmg,Dx
=
1/2mvf2
-
1/2mvo2
vf2 =
2g L cosqmg,Dx
+ vo2
vf =
[2g L cosqmg,Dx
+ vo2]1/2
= [2*10*2*cos53o + 62]1/2 = 7.7
m/s.
Are you surprised? What went wrong with your guess?
Isn't
the acceleration the same in each case?
Why isn't the change in velocity the same?
Here is another throught
question:
Suppose that I drop an object from a given height; the force of
gravity
(the object's weight) does work and the kinetic energy of the
object
increases.
Now, suppose instead that I slowly lower the object slowly from
the
same
initial altitude. Compare the work done by gravity in the
second
case to the work done in the first case.
What about the total work done in
each case?
Conservative and
non-Conservative
Forces
Let's divide the realm of forces in to two categories: conservative
forces and non-conservative forces. This may
seem
rather
facile, in that I could divide forces in to red and non-red
categories,
and each force would have to fit into one of them. However,
this
is a distinction which we will find useful.
There are a number of ways to define what a conservative force
is.
I like to say that a conservative force is one for which the work
it
does
on an object moving from Point A to Point B is independent of the
path
the object takes. Let's take the weight of an object as a
concrete
example. Suppose that I lower a mass m from a height h above
the
table to the top of the table. I'm only interested at this
point
in what the weight does, not what any other force, such as from my
hand,
does. The force is mg downward, and the displacement is h
downward,
and those two vectors are parallel, so we have that
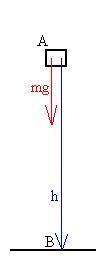
Wg = (mg)(h)(cos0o) = mgh.
Now, let's take the object on a little tour of the region.
Move
it horizontally a displacement s, then down h, then horizontally
again
s', back to point B:
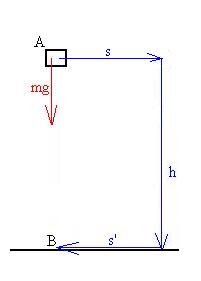
The work done will be
WAB = mg s cos 90o + mg h cos 0o
+
mg s' cos 90o = mgh,
again.
Let's pick a random path:
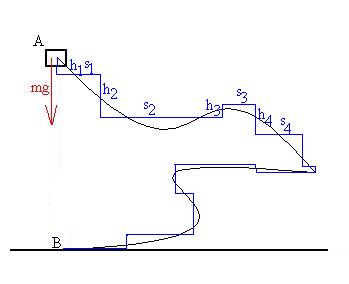
You might be able to see that we can always approximate any path
to
an arbitrary degree of accuracy with these stepped horizontal and
vertical
movements. From previous discussion, we know that any
horizontal
movements will correspond to no work being done by gravity.
The
vertical
displacements are each of magnitude hi , some parallel
to
the
weight and some anti-parallel, such that the work done by the
weight
during
each vertical motion is
Wvertical = Si mg
hi cosqi = mg Si
hicosqi,
where cosqi = +1 if the
displacement
is downward (parallel to the force) and -1 if the displacement is
upward
(anti-parallel to the force).
We realize that Si
hicosqi
= h,
and see that
Wvertical = Si mg
hi
cosqi = mgh,
as before, so that the work done by the weight throughout the
whole
trip is
WAB = mgh,
independent of the path taken.
Let's consider an example of a non-conservative force:
friction.
Consider an object being slid across a table top along two paths
(let
all
Dx's
be the same magnitude):

Remember that we are not concerned with the work done by any other
force, such as that of the hand which pushes the block.
The frictional force will be (not proven here):
Ff = mKmg,
so that the work done by friction from Point A to Point B along
the
direct path is
Wdirect = Ff Dx
cos(180o)
= -mKmg Dx.
Along the indirect path, this will be three times bigger:
Windirect = -mKmg
Dx1
- mKmg
Dx2
- mKmg
Dx3.
= -3mKmg
Dx.
So, we see that friction is not a conservative force.
Potential Energy
Let's consider the dropped pen again. We can say that during
its
fall, the pen is acted on only by the force of gravity, which then
causes
a change in the pen's kinetic energy (work-energy theorem). We
can
develope an alternate notion, by saying that energy is somehow
stored
in
the pen by virtue of its altitude above the table, and that this potential
energy is then converted to kinetic energy as the pen
falls.
The idea of potential energy is really only a bookkeepping device, a
different
way of looking at work. What we find is that any conservative
force
can have a potential energy function associated with it. For
example,
if a conservative force does positive work on an object so that the
KE
increases, we could alternatively say that the PE of the
object
is decreasing while the KE is increasing, and vice versa.
So,
for a given conservative force, Wcons = - DPE.
To do this, we divide the total work on an object into two types,
depending
on whether the force was conservative or non-conservative:
Wcons + Wnon-cons = DKE
- DPE + Wnon-cons = DKE
Wnon-cons = DKE + DPE.
Remember that there may well be more than one conservative force
operating
on the object, which would require us to have more than one DPE
term. Also remember that one should not put the term on both
sides
of the relationship; don't count gravity's effect as both a work
and as
a potential energy.
Can we figure out what the gravitational potential energy
function
is?
Not really. We can only figure out an expression for the change
in the PE. Suppose that we let y be the vertical location of
the
object, and that we lift (or lower) the object by some
displacement Dy.
The force of gravity is of course downward, so if we lift the
object, Dy
is positive, the angle between the weight and the displacement is
180o,
so
the work done is equal to (mg)(Dy) (-1)
=
-mg Dy, while the change in PE is the
negative
of that, or +mgDy. If we lowered
the
object,
the signs of each term (work and DPE)
would
correspondingly reverse. So
DPEgrav = mg Dy,
and it seems O.K. to say that
PEgrav = mgy,
so long as we keep in mind that the assignation of PE = 0 is
arbitrary.
Later, we'll discuss the potential energy from a different
conservative
force.
Conservation of
Mechanical
Energy
In the absence of non-conservative forces, or at least of
non-conservative
forces which do work,
Wnon-cons = DKE + DPE
becomes
0 = DKE + DPE.
Let's write this out more explicitly:
0 = KEf - KEo + PEf - PEo,
which can be re-written as
KEo + PEo = KEf + PEf
.
This says that, in the absence of non-conservative forces (or at
least
of such forces which do work), the total mechanical energy
is conserved.
When
some quantity is conserved, it means that one ends up with the
same
total amount one started with; the energy may change form, but it is
neither
created nor destroyed.
Here are the results of an experiment measuring the PE and KE of an
object as it slides down a frictionless incline (Fadul, Didolkar,
&
Gowda, 2002):
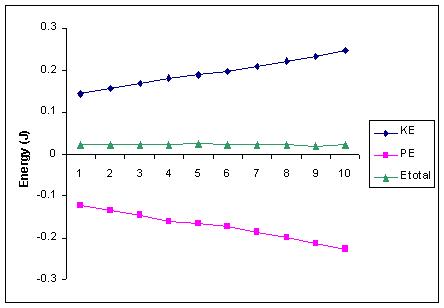
Note that, as the PE decreases, the KE correspondingly increases,
but
that the total energy remains constant (to within experimental
error).
Example:
Consider a block of mass m = 5 kg
at the top of a frictionless ramp L = 2 metres long, which is
inclined
at q
= 37o to the horizontal.
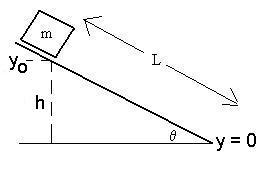
If the mass starts from rest at
the top, how quickly will it be moving when it reaches the
bottom?
Wnon-cons = DKE + DPE
Draw a free-body diagram:

There are two forces acting on the mass: the weight and the normal
force. As before, WN = 0, since the force is
perpendicular to the displacement. On the other hand, the
weight
is a conservative force, and can be dealt with on the right side of
the
equation.
0 = 1/2mvf2
-
1/2mvo2
+ gmyf - gmyo
We can set yf = 0 and then yo = h = L sinq = 2*0.6 = 1.2 m. Then,
0 = 1/2mvf2
- gmyo
1/2mvf2
= gmyo
vf2
= 2gyo
vf2 =
[2gyo]1/2 = [2*9.8*1.2]1/2
= 4.9 m/s, as before.
O.K., you might ask, why bother? The answer should be apparent
in
this example:
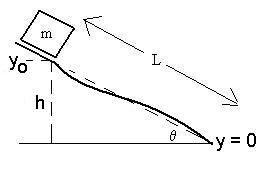
Here, the mass does not slide uniformly down a straight
surface.
The force acting on the mass as it goes down the slide varies as
gmsinq, so the acceleration would not be
constant. Likewise, the work done by the weight on the block
would be difficult to calculate directly (that would require some
integration and we would have to know the exact shape of the
slide.). However, this problem still fulfuills the
requirements for conservation of mechanical energy: since the normal
is
always perpendicular to the path taken, no non-conservative forces
do
any work. We can find the speed of the block at the bottom of
the
slide regardless of the shape of the slide.
This concept of the conservation of mechanical energy is not
quite
the
same as conservation of total energy, which you may have
heard
of
in your other classes. This is a much more restricted form
of
that
concept.
For example, let's look once again at the falling pen. Just
after
release, the pen has zero KE and mgh of PE (we'll let PE = 0 at
the
table
top). Just before hitting the table, the PE = 0 and
the
KE
is not zero, and in fact equals numerically mgh:
KEo + PEo = KEf + PEf
0 + mgh = 1/2mvf2 +
0.
Right after the pen hits the table, it has no PE and no
KE!
What happened to the energy?
Now in a more general way, we can
talk about the conservation of total energy, but only if we
broaden the
definition of energy. You may remember from your other
classes
that
the molecules in solids can be modeled by balls connected by
springs,
and
that the balls are constantly vibrating, possessing kinetic (and
potential)
energy . This KE is different (in a fashion) from the translational
KE discussed above, in that for TKE, every particle shared the
same
velocity
vector, but for vibrational KE, the motions are more
random.
When the pen hit the table, shock waves went out from the impact
through
both the table and the pen, increasing the vibration of the
molecules
in
each object. This increased thermal energy is
observed
macroscopically
as an increase in the temperatures of both the table and
the
pen.
Other energy is carried away as sound, which eventually
warms
other
the objects it hits.
Springs
In this course, at least for now,
we
shall assume that all springs obey Hooke's Law: the force
necessary
to stretch (compress) a spring from its relaxed state is
proportional
to
the amount of stretching (compression). In more mathematical
terms:
F = k (Dx).
The symbol k represents the spring
constant of the spring, the number of newtons requird to
stretch
(compress)
the spring one metre, and is given in N/m. A high value of k
means
that the spring is stiff.
We need to be a bit careful about
signs. The relationship above is the force which needs to be
applied
to
the spring to stretch (compress) it, and that force needs to be in
the
direction of the displacement of the end of the spring.
However,
we are often interested in the force applied by the spring
to
some
other object, which (by the third law) would be in the opposite
direction:
Fon spring = k (Dx)
Fby spring = - k (Dx).
Since we are sometimes in the
habit
of writing down the magnitudes of forces and adding in the
appropriate
signs as necessary, I shall write this relationship this way
F = (-) k(Dx)
with the minus sign there to remind you that the force exerted by
the
spring is in the direction opposite to that in which the spring is
stretched.
Occassionally, the 'delta' is dropped, if it is understood that the
relaxed
position is at x = 0:
F = (-) kx
Is the spring force conservative? A quick look suggests
that
it
is. Since the force exerted by the spring depends only on
the
position
of the end of the spring (we'll assume that the other end is
fixed),
reversing
the displacement back over already covered ground simply undoes
the
work
done the first time (by flipping the sign of the cosine term), so
that
the net work done depends only on the initial and final positions
of
the
end of the spring.
How much work is necessary to stretch (or compress) a spring
distance
x from its relaxed position? We can use the graphical
representation
showing Fon spring as a linear function of x (slope =
k):
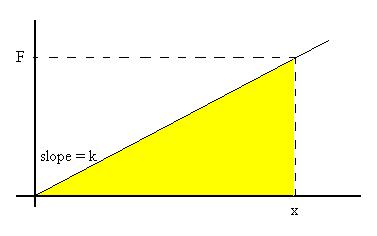
We showed above that the work done by any variable force is
represented
by the area under the curve. Since this is a triangle, the
area
is
one-half the base times the height:
A = 1/2bh = 1/2(x)
(F)
= 1/2(x)(kx) = 1/2kx2.
So, the work done on the spring is 1/2kx2,
the
work done by the spring is -1/2kx2,
and
the change in the PE of the spring is the negative of that, or
DPE = +1/2kx2.
If we define the PE to be zero at x = 0 (the relaxed position),
then
we can say more simply that PEspring = 1/2kx2.
There
are
more notes on this in the solutions to some of the problems.
Power
Power is the rate at which energy is put into, or removed
from,
an object, or the rate at which work is done:
Paverage = dW/Dt.
Pinstantaneous = lim Dt->0dW/Dt.
I use the symbol 'd' for technical
mathematical
reasons having to do with the non-differentiability of work.
We obtain an interesting result if we re-introduce the definition
of
the velocity, v = Dx/Dt:
P = dW/Dt =
[F
Dx
cosq]/Dt =
Fcosq[Dx/Dt]
= Fvcosq.
Without proof, we assert that this is true for instantaneous power
as well; the proof would involve examining the limit as Dt->0.
Examples:
Try Problem 76 in the book:
A 2 kg block situated on a rough incline of 37o is
connected
to a spring of
negligible mass and spring constant k = 100 N/m. The block is
released from rest when the
spring
is unstretched, and the block moves 20 cm down the incline before
coming
to rest. Find the co-efficient of kinetic friction between the
block
and the incline.
Start with the Work-Energy Theorem:
WNC = DKE + DPE
What forces act on the block? There's the weight, the normal
force from the plane, friction, and the spring force. The
weight
and spring force can be treated as potential; energy terms, and
the
normal
force does no work (it's perpendicular to the displacement). The
friction
acts up the plane as the mass moves down the plane (i.e.,
cosqF,Dx
= -1). Use NII to find Ff. Let
perpendicular/upward be
positive y:
N - mgcosq = may = 0
Ff = mKN = mKmgcosq
Then,
-mKmgcosq
Dx = KEf -
KEo
+ PEgf - PEgo + PESf - PESo
Since the mass starts and ends
at
rest, both KE terms are zero. The spring starts out
unstretched,
so PESo = 0, Let y = 0 where the mass comes to
rest,
so
that PEgf = 0.
-mKmgcosq
Dx = - PEgo
+ PESf
= -mgyo + 1/2k[Dx]2
We need to relate the vertical
height
yo to the distance down the plane Dx:
yo = Dx
sinq.
-mKmgcosq
Dx = -mgDx
sinq
+ 1/2k[Dx]2
mK
= [mgDx
sinq
- 1/2k[Dx]2]/mgcosq
Dx = [sinq
- 1/2[k/mg]Dx]/cosq
= tanq
- kDx/2mgcosq
mK
= tan37o - 100(0.2)/2*2*9.8*cos37o = 0.11
Another Example:
Consider a massless spring of
constant
k hanging from the ceiling. Let's attach a mass m and
allow the
mass
to settle very slowly to an equilibrium point.
A) How far does the spring
stretch?
What is the total energy in this situation?
Now, let's raise the mass back
to
the spring's relaxed position and drop it.
B) How quickly is the mass
moving
as it passes through the equilibrium point?
C) How far will the mass drop
before
stopping?
Let's let where the spring is
relaxed
be y=0 and let y be positive upward. When the mass is
first
attached,
the KE is zero (no motion), the PES is zero (the
spring is
relaxed)
and the PEg is zero (because we said so), so the
total
mechanical
energy is zero. Once we lower the mass to its equilibrium
position
and let go, we know that the net force on it is zero:
-mg - kDy
= 0,
so Dy
= yf - yo = yf = -mg/k
It makes sense that this is a
negative
number, since the mass would certainly have descended.
Since the
mass is at rest, there is no KE, and the PES will be
PES = 1/2k[Dy]2
= 1/2k[yf]2 = m2g2/2k
and the PEg will be
PEg = mgyf
= - m2g2/k,
meaning that the total energy
is
ETOT = -m2g2/2k
<
0!
How can this be?
Now, return the mass back to
the
spring's relaxed positon and drop it. What is the total
energy as
it passed through the equilibrium point?
Well, we can write an
expression,
but can't actually calculate it:
ETOT = PES
+ PEg + KE
Now, the PEs we did above: m2g2/2k
+
-m2g2/k = -m2g2/2k
Note that we do expect ETOT
to be zero, since this time there were no non-conservative
forces, and
mechanical energy should have been conserved. So th eKE should
by given
by
KE = ETOT - PETOT
= 0 - -m2g2/2k = +m2g2/2k.
From this, we can find the
mass's
speed as it passes through the equilibrium point:
v = [m/k]1/2g.
Eventually, the mass will stop
(KE
= 0) and then start moving back upward. Where does this
happen (yff)?
ETOT = 0 = KEff
+ PESff + PEgff = 0 + 1/2k[yff]2
+ mgyff
Note that there are two
solutions
to this: yff = 0 (i.e., at the top) and yff
= -2mg/k.
Another Example:
A toy gun launches its projectile by means of a spring, with
unknown
spring constant k. If the spring is compressed 0.12 m from
its
relaxed
position and fired vertically, the gun can launch a 20g projectile
from
rest to a height of 20m above its initial position. Find the
spring
constant k and the speed of the projectile as it passes through
the
spring's
equilibrium position (This is S&F 5-28):
Assuming no friction, we can say that there are no
non-conservative
forces doing work. So,
WNC = 0 = DKE + DPEGRAVITY
+ DPESPRING
0 = 1/2mvf2 - 1/2mvo2
+ mgyf - mgyo + 1/2kxf2
-
1/2kxo2
Here, x represents the amount the spring is stretched or
compressed and
y is the altitude of the ball.
The object starts at rest and ends at rest, so vo = vf
=
0.
Let the vertical reference level be where the spring is relaxed,
so
yo = xo = - 0.12 m, yf = 20m,
and xf
=
0 (the spring is again relaxed):
0 = mgyf - mgyo - 1/2kyo2
1/2kyo2 = mgyf
- mgyo
k = 2mg[yf - yo]/yo2
= 2*0.02*9.8[20 - - 0.12]/(0.122) = 547
N/m
Now, go back and find the speed of the object as it passes the
spring's
relaxation point. Use the same basic relationship:
0 = 1/2mvf2 - 1/2mvo2
+ mgyf - mgyo + 1/2kxf2
-
1/2kxo2
but now, vo = 0, yf = xf = 0,
and
xo = yo = -0.12 m.
0 = 1/2mvf2 + - mgyo
- 1/2kxo2
1/2mvf2 = mgyo
+ 1/2kxo2
vf2 = 2gyo + (k/m)xo2
vf = [2gyo + (k/m)xo2]1/2
= [2*9.8*(-.12) + (547/0.02m)(-0.12)2]1/2 =
19.3
m/s
Yet Another Example:
Consider a skier at the top of a hemispherical knoll of radius R,
which
is covered in slippery snow. He starts from rest at the top
and
travels
down the side. At what vertical distance h from the ground
will
he
become airborne?
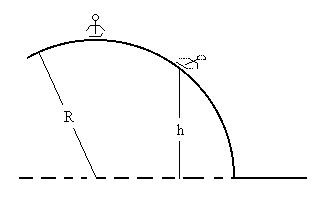
What forces act on the skier? Are any non-conservative
forces
doing work?
So,
WNC = DKE + DPEg
0 = 1/2mvf2 - 1/2mvo2
+ mgyf - mgyo
Let y = 0 at the bottom of the hill so that yo = R, yf
is
then the number h we're asked for, and let vo = 0 (starts
at
rest).
0 = 1/2mvf2 + mgyf
-
mgR
While he is on the slope, his path is circular, and so there is some
combination of forces acting centripetally:

-N + mgcosq = mv2/R
At the point he loses contact with the ground, N = 0:
Rmgcosq = mv2
Pick this as the final situation and substitute into the energy
equation:
0 = 1/2[mgRcosq] +
mgyf - mgR
We seem to have two unknowns, yf and q,
but
they are related in this way:
yf = Rcosq,
so that
0 = 1/2[mgyf ] + mgyf
-
mgR
R = 3/2yf
h = yf = 2/3R
Note 1:
Here is a way of looking at cases of non-constant aceleration (and
correspondingly,
variable forces). Let's break the interval up into N very
short
segments
of displacement such that the acceleration is approximately constant
over
each. Then, for each segment, i, it is still true that
Wi = 1/2 mvif2 -
1/2
mvio2
So, the total work over all of the N intervals would be
WTOT = Si 1/2
mvif2
-
1/2
mvio2
Now, we need to remember that the final speed of one interval will
be the initial speed of the next interval, so all of these terms
will
drop
out except for the first initial speed and the last final speed:
WTOT = 1/2 mvNf2
-
1/2
mv1o2
= 1/2
mvf2
- 1/2
mvo2,
as before.
Note 2:
In three dimensions, we consider the three directions independently,
taking
the components of each force and multiplying by the displacements in
each
respective direction:
WTOT = Si [FixDx
+ FiyDy + FizDz].
All other combinations, such as FixDy
or
FizDx, result in zero work,
since
those force components are perpendicular to the respective
displacement
components.
WTOT = Si FixDx
+ Si FiyDy
+ Si FizDz,
WTOT = [Si Fix]Dx
+ [Si Fiy]Dy
+ [Si Fiz]Dz.
Use Newton's second law in component form:
Si Fix = max;
Si
Fiy = may;
Si Fiz = maz
WTOT = [max]Dx +
[may]Dy
+ [maz]Dz.
For each direction use the corresponding kinematic equation in the
form: v2 = vo2 + 2ad, to get
WTOT = m*1/2[vx2 -
vox2] + m*1/2[vy2
-
voy2] + m*1/2[vz2
-
voz2].
Re-arrange terms to get
WTOT = 1/2 m[vx2
+
vy2 + vz2 - vox2
- voy2 - voz2]
=
1/2 m[vx2 + vy2
+ vz2] - 1/2 m[vox2
+
voy2 + voz2]
WTOT = 1/2 mv2 -
1/2
mvo2
as before.
Return
to
Notes
Directory
Continue
to Next Section
of Notes
D. Baum 2000














