Section 1-10 - Oscillations
Mass on a Spring
Simple Pendulum
Damped Oscillations
Resonance
Correlation
to your Textbook
Mass on a Spring
We started by examining a mass on a spring, placed horizontally on a
friction
less table, so that gravity and the table's normal force cancel,
leaving
the spring force as the only one to act on the mass. We know from
previous discussion that the spring follows Hooke's Law, F = - kx, the
force applied to the mass is proportional to the displacement of the
mass
from the equilibrium point and is directed opposite to that
displacement.
In general, a force which is directed opposite to the displacement, but
not necessarily proportional to it, is called a restoring force,
since
it
acts to return the object to its original position.
If we disturb the mass from the equilibrium point, it will oscillate
about that point with a well defined frequency,
f, which we find
experimentally
is independent of the degree of disturbance (i.e., pull the mass
a little ways from the eq. pt, or a long ways, and the frequency of
oscillation
is the same.). We would like to determine that exact mathematical
function that the displacement follows, x(t), and see if there is a way
to predict the frequency of the oscillation.
Let's write Newton's Second Law for this mass:
S Fi = ma
- kx = ma
Remember that a = d2x/dt2, so
d2x/dt2 = - (k/m) x.
So, we're looking for a function x(t) which is proportional to its
own
second time derivative. Two general types come to mind: x(t) = Aeat
and x(t) = A cos(2pf t + f)
(here,
f is called the phase angle and merely allows us to
convert the cosine function into a sine function, or into a combination
of the two).
Let's try each by substituting into the differential equation:
x(t) = Aeat
dx/dt = aAeat
d2x/dt2 = a2Aeat
Then,
a2Aeat
= - (k/m) Aeat
a2 = - (k/m) , if we assume that
A is not zero, otherwise, it's an uninteresting solution!
Oops! Looks like a will be imaginary,
which isn't good for a real physical system (see Note below).
Let's try the other
possible solution:
x(t) = A cos(2pf t + f)
dx/dt = - 2pf A sin(2pf t + f)
d2x/dt2 = - (2pf)2A
cos(2pf t
+ f)
Then,
- (2pf)2A
cos(2pf t
+ f) = - (k/m) A
cos(2pf t
+ f)
- (2pf)2
= - (k/m) , again assuming that A is not zero.
This looks O.K. The frequency of oscillation is f
= [1/2p][k/m]1/2.
We often talk of the angular
frequency, w, given by w = 2pf. Therefore, w = [k/m]1/2.
We also took this result and found an expression for the period, T,
of the oscillation. The period is the amount of time necessary to
complete one cycle. We know that the normal frequency f =
w/2p
represents the number of cycles per second, so the period is clearly
T =1/f = 1/(w/2p)
= 2p/w = 2p[m/k]1/2.
N.B.: The fact that a comes out
imaginary
isn't really so much of a problem. We define eiat
= cos(at) + i sin(at), where here, i is the square root of -1. We
can verify this by expanding each term in a Taylor's series about t =
0. The solution to this differential equation is a combination
of eiat and e-iat
which can be made to come out equal to a combination of sin(at)
and cos(at): x(t) = A cos(at +
f) .
We noted two things here. First, the frequency appears to be
independent
of the amplitude of oscillation, so it doesn't matter how far I pull
the
mass before I release it, the mass will oscillate with the same
frequency.
This type of frequency, at which a system 'prefers' to oscillate, is
called
the natural frequency. Second, the frequency depends on
the
mass and stiffness of the spring, which we then tested qualitatively.
This type of motion, x(t) = A cos(wt
+
f), is referred to as simple harmonic
motion.
When the spring is horizontal, Newton's second law is
Si Fi = - kx
= ma,
and the motion is as described above. What if the spring had
been oriented vertically, so that gravity were not cancelled? The
new
equilibrium point would be where the weight and the spring force
balance:
Si Fi = -mg
- kxEQ = 0 xEQ
= -mg/k (negative, because this equilibrium point is below the
'no-gravity'
equilibrium point).
Now let the mass oscillate. Let x' be the displacement from the
new equilibrium point, such that x' = x - xEQ.
Substitute.
Si Fi = -mg
- kx = ma
-mg - k (x' + xEQ) = ma
-mg - kx' - kxEQ = ma
[-mg - kxEQ] - kx' = ma
The quantity in brackets is known to be zero, so
- kx' = ma,
which is the same force equation (and therefore the same motion) for
the case of no gravity, except that the equilibrium point will be where
x' = 0, that is, at x EQ.
Let's see if we can determine any information about the mass's
velocity
and acceleration. We said that x(t) = A cos(wt
+
f), so
v(t) = dx/dt = d/dt[A
cos(wt
+ f)] = - wA
sin(wt
+ f).
a(t) = dv/dt = d/dt[-
wA sin(wt
+ f)] = - w2A
cos(wt
+ f)
For fun, what will be the fuctional forms for the jerk, kick, and
lurch?
j(t) = w3A sin(wt
+ f)
k(t) = w4A cos(wt
+ f)
l(t) = - w5A sin(wt
+ f)
Simple Pendulum
There are many other systems which exhibit simple harmonic motion
(SHM),
and even more which are close enough that we can make use of the
results
above for a reasonably correct approximate solution. One such
system
is the simple pendulum, which is a point mass m at the end of a
massless string or stick of length l. Let's look at the
free
body diagram for such an object.
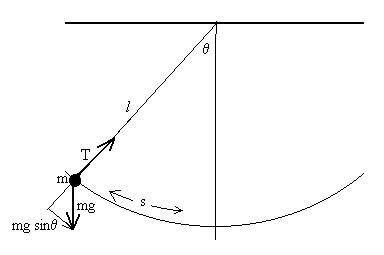
We are interested in the motion along the circular arc. Let us
describe the bob's position with s = lq,
the
displacement
along the arc which we shall make positive to the
right
and negative to the left. Break the forces into tangential and
radial
components. Radially, we have
T - mgcosq = maC,
where aC is the centripetal acceleration. We're not
really interested in this.
Tangentially, we have
Ft = mg sinq =
mg sin(s/l).
We note that the force is really a restoring force, since it points
in the opposite direction along the arc as the bob's
displacement.
Let's add the minus sign as we did for the mass/spring system to
account
for the direction of the force:
Ft = - mg sin(s/l).
Now, this is not the same as the for the mass/spring system,
since F is proportional to the sine of the displacement, not to
the displacement itself. However, if an angle is small, the sine
of the angle is approximately equal to the angle itself. So we
can
make an approximation:
Ft = - mg (s/l) = - (mg/l) s.
Now, the restoring force is at least approximately of the form F =
- Cx, and we can make use of the result above. Let's compare the
two systems
F = - (k) x, where w = [k/m]1/2
F = - (mg/l) s,
so that it's clear that (mg/l) takes the place of k. Let's
substitute it into the result we already have for w:
w = [(mg/l)/m]1/2
= [mg/lm]1/2 = [g/l]1/2,
which is indeed the correct answer. In class, we tested
qualitatively
the dependence of the frequency on the length, and the independence on
the mass, and found agreement with the theory; we could not test the
dependence
on gravity, however.
In fact, you may remember back to the beginning of the year when we
discussed dimensional analysis. We looked at all of the
quantities
which might possibly affect the period of oscillation: mass m: [M],
string length l: [L], and gravity g: [L]/[T]2.
We saw that the only combination which could result in the dimensions
of
the period, [T] , is [l / g]1/2, or {[L]/[T]}-2
[L]1/2.
Above, we found that the period of oscillation
for a simple pendulum is
T =1/f = 1/(w/2p)
= 2p/w = 2p[
l
/
g]1/2.
Here is another example for you to work on:
Consider a torsional pendulum, a cylinder hanging from a
string.
The torque necessary to twist the string is assumed to be proportional
to the angular displacement:
t = - k q.
The cylinder is twisted through some initial angle, then
released.
What is the natural frequency of rotational oscillation of this system?
Now, two more considerations:
Suppose that the angle of oscillation of a pendulum is greater than
what we consider small. How would we find the period in that case?
This is a difficult calculation, and one which I think is only worth
setting up, not necessarily solving.
Consider the time t necessary for the bob to move from its greatest
displacement at qo to the bottom
of its arc. Then, in time interval dt, the bob moves a distance ds (=L dq)
along the arc, such that
dt = ds/v.
We can find an expression for the speed by using conservation of
mechanical energy (Tension does no work, weight is converted to a PE
term):
mgho = mgh + 1/2mv2
v = [2g(ho - h)]1/2
From a previous problem, we know that h = L(1 - cosq),
so
the
speed becomes
v = [2gL(cosq - cosqo)]1/2
and so
dt = L dq/[2gL(cosq - cosqo)]1/2
Now, integrate over the quarter trip from the maximum displacement to
the bottom of the arc:
0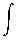 T/4
dt = [L/2g]1/2 qo
T/4
dt = [L/2g]1/2 qo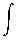 0 dq /
[(cosq - cosqo)]1/2:
0 dq /
[(cosq - cosqo)]1/2:
T = 4 [L/2g]1/2
qo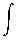 0 dq /
[(cosq - cosqo)]1/2
0 dq /
[(cosq - cosqo)]1/2
At which point, I think I leave this for you to solve, if you're
interested. The final answer is in your textbook.
Physical pendulum
One might also consider a pendulum not comprising a pointmass
and light string. Consider an object of mass m, suspended from
one end. The center of mass of the object is a distance D
from the pivot. What will be the period of oscillation of the
object?
We can assume that the weight of the object acts at the object's
centerof mass. If the object is moved at angle q from the vertical, then the weight exerts a
torque about the top end of
t = - mgD sinq.
From NII for rotation, we can write that
t = Ia = I d2q/dt2
If we again assume that the
angle is small, this becomes
d2q/dt2
=
-
(mgD/I) q
with a solution we now know well:
q (t) = qo
cos(wt
+ f)
Compare this to the equation for a mass and spring:
d2x/dt2 = - (k/m) x.
and we see that
mgD/I = k/m = w2,
so that the frequency of oscillation is
w = [mgD/I]1/2
and the period is
T = 2p[I/mgD]1/2
Example:
Consider a thin rod of length L and mass M rotating about an axis
through an end. Then I = 1/3ML2
and D = L/2. T is then
T = 2p[1/3ML2/Mg(L/2)]1/2
= 2p[2L/3g]1/2
One last term: RG the
radius of gyration. The
radius of gyration of an object of mass M is the distance from the
rotational axis a point mass M should be placed in order to have the
same moment of inertia as the original object:
MRG2 = I
RG = [I/M]1/2
This is not
necessarily the length lEFF
of a simple pendulm that will have the same period, which is lEFF = I/md
Example:
the radius of gyration for the rod above is
RG = [1/3ML2/M]1/2
= [1/3]1/2L.
Damped Oscillations
We spoke briefly about damped oscillations. The
equations
above suggest that, if one sets the mass/spring system into
oscillation,
the total energy of the system remains constant and the mass will
vibrate
forever with the same amplitude. In fact, we know that the
mass will slow a bit on each pass due to friction with the air (usually
assumed to be a drag force of the form Ff = -bv,
although constant friction from a tabletop is another possibility);
energy is removed as friction performs negative work on the
mass.
- kx - b dx/dt = m d2x/dt2
We shall not discuss the actual solution to this differential equation
here. However, the solutions fall into two basic categories.

The figure shows a lightly damped system (black curve) and an
overdamped
system (red line), which loses so much energy so quickly that it never
oscillates even once. A good example of the overdamped system is
the car shock absorber. The car (m) is supported by springs (k),
so that SHM is possible. If one were to drive over a bump with
faulty
shocks, the car would then continue to oscillate at about 1 Hz for
several
seconds. Shock absorbers dampen the system so that the ride
smooths
out without the oscillations.
One caveat: the natural frequency of a lightly damped oscillation is
slightly different than the value of an undamped oscillation:
w ' = [(k/m) - b2/4m2]1/2,
where b characterizes the amount of damping.
Let's verify that this is correct:
Let x(t) = Aeiat
Substitute this into the differential eq with damping:
- kx - b dx/dt = m d2x/dt2
- kAeiat - b iaAeiat
= (i2)a2 m Aeiat
and simplify:
a2 m - iba -
k = 0
which is a quadratic equation in alpha. Solve this using
the standard solution formula:
a = [- -ib +/- ( (- ib)2 - 4m(-k))1/2/[2m]
= ib/2m +/- (k/m - b2/4m2)1/2
Now, if we put this back into the assumed solution, we get an
oscillating part and an exponentially decaying part:
x(t) = Aeiat = A e-bt/2m
exp( - i (k/m - b2/4m2)1/2
t) = A e-bt/2m cos((k/m
- b2/4m2)1/2 t +
f).
We can even see now the transition pouint from oscillatory to
overdamped motion:
b2/4m2 > k/m ->
b > 2(km)1/2.
Resonance
We returned to the notion of the natural frequency of a system.
If
one were to disturb the mass/spring system in some way and step back,
the
system will oscillate with natural frequency wo
= [k/m]1/2. If it's disturbed again in a different
manner,
the system will still oscillate at that same natural frequency, until
its
energy is depleted (see damped oscillations).
If
we
want the system to continue to oscillate, we must replace the
energy
lost to dissipative forces. Let's jiggle the other end of the
spring,
applying a force though a distance (i.e., doing work), at some
frequency
w,
which is then known as the driving frequency. Let us vary
the driving frequency to see the effect on the system. If we
jiggle
the spring at a very low frequency, we see that the mass oscillates
with the same frequency at which it is driven, but with a small
amplitude.
Changing to very high driving frequency, we see once again that the
mass oscillates at the driving frequency, but with a very small
amplitude.
However, if we excite the system at a driving frequency very near to
the
natural frequency, we see that the response of the system, as
demonstrated
by the amplitude of oscillation, increases. If we plot this
response
as a function of the driving frequency, we see the curve shown here:
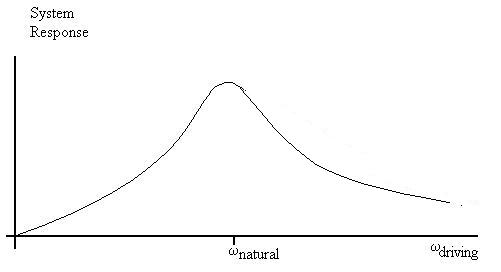
The condition when the system is driven at its natural frequency and
delivers its greatest response is called resonance.
Sometimes
resonance is desirable, sometimes not. For example, if one wants
to push a small child on a swing, the greatest amount of fun (or
terror)
is attained when one pushes the swing at its natural frequency.
On
the other hand, if the ground shakes at the natural frequency of a
skyscraper,
the building may respond with an amplitude beyond the limits of
structural
integrity. The Tacoma Narrows Bridge collapse, which was featured
in an Alpine Stereo advertisement several years ago, occured because
the
wind passing over the bridge excited one of the span's torsional
oscillation
modes, resulting in the collapse about three hours later. The
speed
of the oscillations was speeded up for the advert, but the amplitude of
the oscillations was not. Are you surprised at the incredible
elasticity
of steel and concrete? Only a dog lost its life in the collapse,
because the owner left it behind when he abandoned his car on the
bridge
(Hmm!). The bridge had exhibited strange effects for the three
months
it was open. There are films of the deck of the bridge
oscillating
in a vibrational mode much like waves in the ocean; cars could actually
disappear from view behind the humps which rose and fell in the
roadway.
A related system is that of tall skyscrapers. Once again, if the
wind were to gust at the natural frequency of the building, it might
cause
collapse; modern buildings often have a mechanism to 're-tune' the
vibrational
modes of the building away from the current driving frequency of the
wind.
Return
to Notes Directory
Continue
to Next Section of Notes
D Baum 2000


