Section 1-11 - Waves and Sound
Speed of Mechanical Waves
Reflections of Pulses
Sinusoidal Waves
Properties of a Wave
Standing Waves
Non-Sinusoidal Waves
Intensity
Beats
Doppler Effect
Notes: Sound in Solids, Trig
Identity
Correlation to
your Textbook
Speed of Mechanical Waves
We covered single oscillators in Section 1-10. For the specific
example
of a mass/spring system, we saw that there is a natural frequency at
which
the system would 'like' to oscillate, given by wo
= [k/m]1/2, or rather, the period T = 2p[m/k]1/2.
Now,
let's consider a chain of such oscillators, identical masses
connected
by identical springs:

If we apply a disturbing impulse to the end oscillator, it will move
to the right, applying its own force on the next mass, et c.
The
speed of this disturbance as it moves down the chain of oscillators
should depend inversely on the period of oscillation of each mass, i.e.,
be
proportional to the natural frequency [k/m]1/2.
We can guess, then, that the speed of any mechanical wave in a material
should be proportional to [elastic property of material/inertial
property
of material]1/2. For example, the speed of a
sound pulse in a solid is found experimentally to be v = [Y/r]1/2,
where Y is the Young's modulus, a measure of the springiness of the
material,
and r is the mass density of the material
(inertial
property). See below for a more
mathematical
justification of this relationship. The speed of sound in a fluid
(like air) also follows this form: v = [B/r]1/2,
where
B is the bulk modulus, a measure of the elastic
properties
of a fluid.
Derivation for the specific case of a chain of oscillators:
Let x be the equilibrium position of each mass. The masses are
separated at equilibrium by distance D. Let y(x, t) be the
displacement of each mass from its proper position.
Consider Newton's Second Law for the mass at position x + D.
Fx+D = max+D = m d2y/dt2|x+D
NB Here I use delta to indicate a partial
derivative.
The force is due to the springs on either side of the mass (Hooke's
Law), but the amount each spring is stretched or compressed depends on
the locations of both of the masses:
Fx+D = k[y(x+2D, t) - y(x+D, t)] - k[y(x+D, t) - y(x, t)]
Combine these expressions, divide each side by m, factor the k, and
multiply the right side by D2/D2:
d2y/dt2|x+D
= [D2 k/m] [[y(x+2D, t) - y(x+D, t)]/D -
[y(x+D, t) - y(x, t)]/D]/D
Now, let's define some new quantities:
KEFF = k/N is the effective spring constant for N of the
oscillators.
L = ND is the length of the chain of N oscillators.
M = Nm is the mass of N oscillators.
So,
d2y/dt2|x+D = [KEFFL2/M]
[[y(x+2D, t) - y(x+D, t)]/D - [y(x+D, t) - y(x, t)]/D]/D
Now, let's smooth the system out by taking a limit D-> 0 by
letting N go to
infinity while D and m go to zero:
lim D-> 0 d2y/dt2|x+D = [KEFFL2/M]
lim
D-> 0 [[y(x+2D, t) - y(x+D, t)]/D - [y(x+D, t) - y(x, t)]/D]/D
The expression in red then becomes the derivative of y wrt x,
evaluated at x+D, and the blue expression is the derivative of y at
x. The left side simply becomes the second derivative at x.
d2y/dt2|x
= [KEFFL2/M] lim D-> 0 [dy/dx|x+D - dy/dx|x]/D
The limit that remains is the derivative wrt x of the derivative of
y, or
in other words, the second derivative of y wrt x evaluated at x:
d2y/dt2|x
= [KEFFL2/M] d2y/dx|2x
This then results in a version of the wave
equation:
d2y/dx2
= [M/KEFFL2] d2y/dt2.
We'll come back to this result in a while.
Properties of a Wave
Let's consider a disturbance that repeats itself at regular
intervals. Instead of pulses, the driving force at the end of the
medium in which the disturbance travels is periodic, i.e., it repeats its motion in a
given amount of time, T. Now, the wave which is produced will
have the same frequency as the
driving
force, even though the speed of propagation will be determined by the
natural
frequency of the individual oscillations (yet to be proven).
Mechanical waves in
general
are often classified as longitudinal or transverse.
Waves
in which the individual pieces of the medium move along the same
line as the direction of propagation of the wave are referred to as longitudinal,
while
waves in which each piece of material moves along a line
perpendicular
to the direction of propagation, such as on a taut string, are called transverse.
We
demonstrated each of these with the slinky.

We describe waves using several quantities:
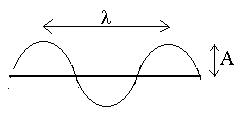
- the frequency (f or sometimes n)
counts
how many oscillations each piece of material experiences each
second,
or alternatively, how many peaks pass by an observer each second.
- the amplitude (A) describes the maximum deviation from
equilibrium.
This is easy to visualize in the example above where A refers to the
maximum
displacement, but it can also refer to the maximum excess of pressure
over
average atmospheric as in sound, or the maximum electric field strength
as in light, et c.
- the speed (discussed above).
- the wavelength (l) measures the
physical distance
between correponding points on adjacent waves (e.g., from peak
to
peak).
There is a relationship among f, l,
and v, which we can deduce from the 'railcar analogy.'
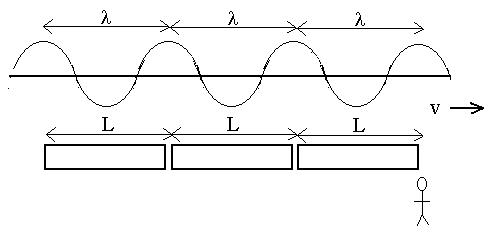
Suppose that a train with cars of length L passes you at speed v.
You count N cars in time t. The distance traveled by the train in
that time is NL. The speed of the train is v = d/t = (NL)/t =
(N/t)L.
We recognize (N/t) as the frequency f and L as the analog of l,
so v = fl.
Sinusoidal Waves
Let's consider a special case in which the driving force is sinusoidal.
Although we won't prove it, sinusoidal waves are described
mathematically
by the expression:
y(x,t) = A sin(2px/l
-/+ 2pf
t
+ f),
where f
is
a phase angle which allows us to change the function to cosine or to
some
combination of sine and cosine. This is sometimes written this
way:
y(x,t) = A sin(kx -/+ wt
+ f).
The quantity k above is the
magnitude
of the wave vector, which is then 2p/l.
In
both cases, the negative sign indicates a wave moving the the right
(positive
x) and the plus sign indicates that the wave is moving toward the left.
Let's check this out. If we choose a particular time, then the
function looks like this (here, I'm combining the now constant time
term
with the phase angle and renaming the combination as a new phase
angle):
y(x) = Asin(2px/l
+ f'),
that is, a snap shot of the wave at that instant. We see that
the wave has a sinusoidal shape with regard to position, x, and that as
x increases by one wavelength, the function advances by one cycle.
On the other hand, if we look at what's happening at a particular
location
x (again, I'll include the now constant spatial term into a new phase
angle),
the function looks like this:
y(t) = Asin(wt +f"),
that is, that piece of the medium at that particular location undergoes
simple harmonic motion. These results are at least consistent
with
our notions about the wave.
We see that the wave has a combined spatial and
temporal
dependence, since both x and t occur in the argument of the sine
function.
How does this correspond to a moving wave? The crest (for
example)
of the wave will occur when the argument of the sine function equals p/2
radians (or p/2 + 2np,
n
an interger, depending on exactly which peak we want to consider):
kx - wt +
f = p/2.
The position x at which this peak occurs is then given by
x = [p/2 - f]/k+
[w/k]t,
so that, as time progresses, the location x of the crest must become
more positive, that is, the crest moves to the right. If the sign
between the two terms had been positive instead, then the value for x
would
have to become more negative as t increases, so that the crest moves to
the left.
NOTE: Even though we are using transverse waves on a string as our
model
for wave behaviour, these properties can be ascribed to just about any
type of mechanical wave. We just let the displacement from
equilibrium
represent, for example, the deviations from atmospheric pressure (for
sound)
or angular displacement (for torsional waves). We can even talk
about
variations in the strengths of electric and magnetic fields in this
way.
Now, let's see if our sinusoidal wave function is a solution to the
wave equation:
y(x,t) = A sin(2px/l
-/+ 2pf
t
+ f),
dy/dx = [A2p/l] cos(2px/l
-/+ 2pf
t
+ f)
d2y/dx2
= -A[2p/l]2 sin(2px/l
-/+ 2pf
t
+ f)
l2 d2y/dx2 = -A[2p]2 sin(2px/l
-/+ 2pf
t
+ f)
dy/dt = -/+ [A 2pf] cos(2px/l
-/+ 2pf
t
+ f)
d2y/dt2
= -A[2pf]2 sin(2px/l
-/+ 2pf
t
+ f)
f -2 d2y/dt2
= -A[2p]2 sin(2px/l
-/+ 2pf
t
+ f)
Equating the last two results:
l2 d2y/dx2 = f
-2 d2y/dt2
d2y/dx2 = [lf] -2 d2y/dt2
You may remember that lf is
the wave's velocity, so our wave equation becomes:
d2y/dx2
= [v] -2 d2y/dt2
So, the constant of proportionality is the square of the wave's
velocity. This will be true for any type of wave we study.
Is it restricted to waves that are sine or cosine functions?
No. We will make use of a technique called Fourier decomposition and argue
that any well behaved wave shape can be written as a sum of sine and
cosine terms, each of which independently solves this wave equation.
Non-Sinusoidal Waves
We've been concentrating on sinusoidal waves. What about waves
that are not sinusoidal? Most wave shapes can be approximated by
adding
up different amplitudes of many sinusoidal waves of different
frequencies
(Fourier decomposition):
Y(t) ~ Sn An sin(nwt)
with n = 1, 2, 3, ...
We can represent these amplitudes An graphically with a
figure like this one, similar to what was shown on the screen of the spectrum
analyzer).
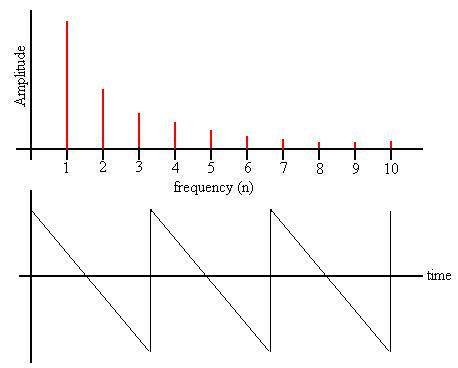
For example, a 'ramp' wave is composed of waves with the form An
sin(nwt) with n = 1, 2, 3, ... and the
amplitude
An decreasing as 1/n.
Or, a square wave is the sum of waves of the form An sin(nwt)
with n = 1, 3, 5, ... and the amplitude An decreasing as
1/n.
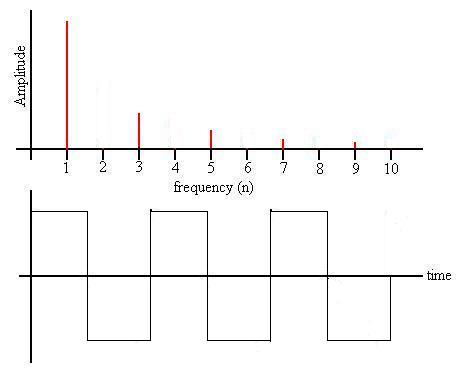
Or, a triangular wave is the sum of waves of the form An
sin(nwt) with n = 1, 3, 5, ... and the
amplitude
An decreasing as 1/n2.
Go to the Excel
workbook
again and try some combinations of harmonics to see if you can
duplicate
these waveforms on the Fourier Demo worksheet. Enter the
amplitudes
of the various harmonics and observe the resulting wave shape.
To wrap it all up, the functions describing waves, in one dimension
at least, generally are solutions to the wave equation:
d2y/dx2
= [v] -2 d2y/dt2.
Special case - tranverse waves on a string
Consider a small length Dx of string a
distance x from the end on which a transverse wave is traveling.
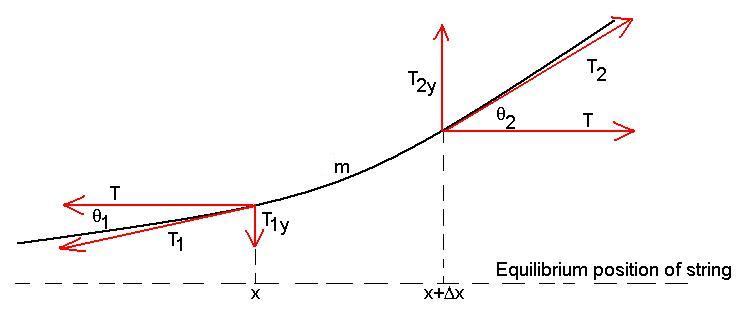
The mass of this small piece of string is m. The forces acting on m are shown in the figure
above. Each end of m is
pulled by the adjacent piece of string along a line tangent to the
string at the end (T1 and T2). Each of
these forces can be broken up into components; since we do not expect
any motion in the horizontal direction, those components (T) should
cancel, and individually should be equal to the tension in the
string. The vertical components will act to accelerate m. Let's find them:
T1y / T = tanq1
T2y / T = tanq2
Let's remember that the tangents of these angles are the slopes of the
curves at those points, so
T1y / T = dy/dx|x
T2y / T = dy/dx|x+Dx
Use NII:
Si Fyi = may
T2y - T1y = T [dy/dx|x+Dx - dy/dx|x] = m d2y/dt2
Divide both sides by T Dx.
[dy/dx|x+Dx - dy/dx|x]/Dx = [m/TDx] d2y/dt2
Note that m/Dx is the linear mass
density, l. To avoid confusion in
this section, however, we will use m = m/Dx.
Take the limit of Dx -> 0. We've
already seen an example of this; the left side becomes the second
derivative of y wrt x.
d2y/dx2
= [m/T]
d2y/dt2
Comparison with previous results then indicates that the speed of this
wave along the string is
v = [T/m]1/2.
Reflections
We next looked at reflections of pulses in a string. We noted
that
a pulse traveling down the string is reflected with the same
orientation
if the end of the string is free to move, and reflected with an
inverted
orientation if the end of the string is fixed. Although this
could
be proven mathematically, we based our assertion on experiment.
We
can visualize what's happening, however, by imagining that the string
continues
beyond its actual end, and that an imaginary wave is traveling back
down
the string towards the end from the imaginary side. We invoke the
principle
of superposition, the notion that the total displacement of the
medium
is the sum of the individual displacements due to each pulse; in this
way,
we know that the reflected pulse for a fixed end must be inverted,
since
this is the only way the total displacement at the end of the string
can
always be zero, and then clearly, the wave and its reflection must add
together in the case of a free end.
I have no animation for this yet, but download this Excel
workbook, go to the 'reflection demo', choose 'Enable Macros,' and
press 'Ctrl Z' to advance the simulations. The dark line
represents
the actual string, the coloured lines the real and imaginary pulses on
it. Reset the demo by pressing 'Esc' and typing '0' in the black
box.
Now, instead of considering the two extreme cases (completely fixed
or completely free ends), think about what would happen if the string
were
tied to another string. In all cases, we would expect that some
of
the wave would continue down the second string with the same
orientation
(and frequency) as the original wave; this is called the transmitted
wave. We also notice that there is a reflected wave,
the
orientation (and size) of which depends on whether (and by how much)
the
second string is 'heavier' or 'lighter' than the first. The
quantity
used to measure the difficulty of a wave in passing through some medium
is called the impedance, Z. If Z2>Z1,
the
reflected wave is inverted; if Z2<Z1, the
reflected wave is upright. This is a general result, even though
the exact values of the impedances are calculated in different ways for
different media. In the specific example of transverse waves on a
string, we have that (asserted without proof)
Z = [Tm]1/2.
In that case, we see that our original examples correspond to Z = 0
(end of string loose, so m2 = 0)
and Z = infinity (end of string tied to wall, so m2
=
infinity).
What would happen if the two media had the same impedance?
The impedances also tell us how much energy is reflected and how
much
is transmitted:
Some other day....
Standing Waves
The principle of superposition states that, if more than one
wave
is passing through a givien point, the total displacement is the linear
sum of the displacements due to each individual wave.
Suppose that we set up two sinusoidal waves in a (one dimensional)
medium which are identical in every way except their directions.
An example would be two waves moving along a very long string, each end
being jiggled at the same amplitude and frequency. What happens
when
these waves meet? (In class, we made use of a wave I generated in
the string, and that wave's reflection.
We use the principle of superposition to find the result by adding
the two individual waves. We saw that the resulting wave did not
appear to travel at all; this type of wave is called a standing wave.
Let's
examine this more mathematically:
y1 = A sin(kx - wt) and
y2 = A sin(kx + wt).
ytotal = y1 + y2 = A sin(kx - wt)
+ A sin(kx + wt).
ytotal = A [sin(kx) cos(wt) -
cos(kx) sin(wt)] + A [sin(kx)cos(wt)
+ cos(kx) sin(wt)],
where we have used the trig identity sin(a + b) = sin(a) cos(b) +
cos(a)
sin(b).
Re-arranging results in
ytotal = 2A sin(kx) cos(wt).
Here, we see that, in contrast to the original waves which had mixed
spatial and temporal components, this wave has separate spatial and
temporal
components. Each piece of the medium undergoes SHM, but with an
amplitude
which depends on its position.
y = [2A sin(kx)] cos(wt).
We can see that there are spots which never oscillate (nodes)
and spots which have maximum oscillation (anti-nodes).
Each
type of location is separated from its adjacent neighbour by one-half
of
the wavelength.
In our class demonstration, we used reflected waves as the second
wave.
But in systems with finite length, there will be many reflections from
each end which will have to be added to determine the overall shape of
the string. We started with a string fixed at each end, and we
excited
the waves with different frequencies. In some cases, we noted
that
the waves all added up to a random pattern, eventually canceling
out.
In other cases, we saw that the intial and reflected waved added to
produce
a standing wave. What conditions need to be met to do this?
We could do a very mathematical derivation of this, but it is just as
correct
to base our investigation on the experimental data.
String fixed both ends:
We saw a series of patterns like those shown below as we increased
the frequency at which the system was excited. The lines indicate
the limits of the oscillations of the string (the envelope).

We noticed that in each case, the length of the string L was a positive
integer multiple of half of the wavelength,
L = nl/2, n = 1, 2, 3, ....
We can convert that to frequency by remembering that f = v/l,
so that
f n = nv/2L.
We do the demonstration again with one end free, and find patterns
like these:
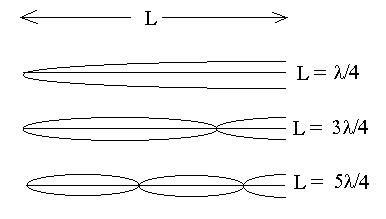
such that L = nl/4, n = 1, 3, 5, ..., which
then becomes f n = nv/4L.
Lastly, we image what might happen if we could have a string free at
each end. This might seem impossible, but remember that we can use the
concept for a number of other systems which do meet this criterion, for
example, sound waves in a tube open at each end where the air is free
to
vibrate back and forth.
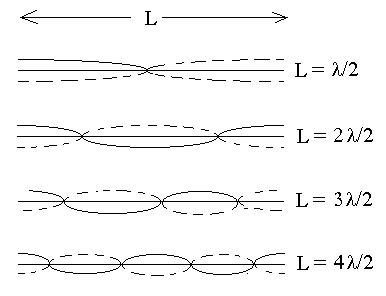
We see that the results here are identical to the case of fixed both
ends, just with the positions of the nodes and anti-nodes exchanged.
We see that, unlike for a single oscillator with a single natural
frequency,
we here have a system with many natural frequencies:
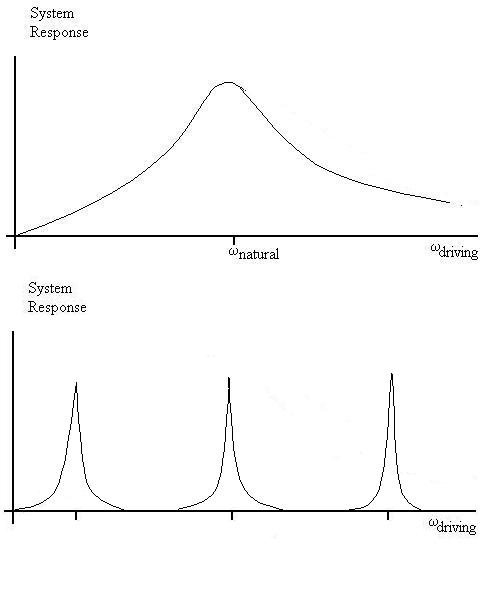
Remember that, even though we derived these results for transverse
waves on a string, the results are valid for other system. For
example,
consider a stopped organ pipe, which means that it is open at one end
and
closed off at the other. At the open end, air is free to vibrate,
while at the closed end, no vibration is possible because of the
stopper.
This pipe will support standing waves of the form f n
= nv/4L, n = 1, 3, 5, .... How are these frequencies
produced?
In an organ , air is pumped into the pipe against a sharp edge, which
produces
all frequencies. However, those frequencies which do not
correspond
to the favoured frequencies reflect back and forth in the pipe and, on
average, cancel themselves. But the few special frequencies
re-inforce
one another and produce standing waves. These frequencies are
often
referred to as the harmonics of the system. On occasion,
they
are referred to as the fundamental
(n = 1) and the overtones
(n > 1).
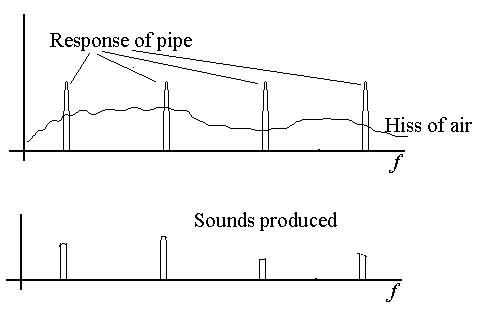
Now here's a question. How can a listener distinguish different
musical instruments which are playing the same note? For example,
an oboe and a clarinet are both essentially cylindrical tubes, closed
at
one end and open at the other, and so they produce the same sequence of
harmonics, fn = nv/4L. The answer is that they
each put slightly different amounts of energy into the different
harmonics,
and it is that distribution that your brain remembers and labels as one
instrument or the other (see
below).
FIGURE
Also, it is possible to suppress certain harmonics. For
example,
we managed to suppress all odd harmonics on a string fixed at both ends
simply by grabbing the middle of the string, thus forcing a node to
form
there; any harmonics which do not have a node there do not form.
We also investigated the suppression of harmonics in an aluminum rod;
by
grasping the rod at different points, we could make the sound the rod
makes
when struck different. This technique is used in the forked
fingerings
of woodwinds, and in the 'nodal vents' used in some reproduction
natural
trumpets.
Intensity
A wave can be defined as a transfer of energy without a net movement of
matter. For sound (and later, light), we measure the rate of
energy
transfer per unit area as the intensity, I, with the
corresponding
units of watts/m2. Consider a fire siren which
broadcasts
isotropically P joules of sound energy per second. Draw an
imaginary
sphere of radius R with the centre at the siren; all the energy must
pass
through that sphere, and the intensity will be
I = P/4pR2.
We see that if we make the sphere larger, the energy will be
distributed
over a larger area, and the intensity will be reduced (that is, each
square
metre of area will receive less energy). This 1/r2
dependence is fairly common, and we shall see it again.
An alternate way of expressing intensity is in units of decibels.
The
decibel scale is is logarithmic, and thus follows more closely the
actual size of the signal sent from human ear to human brain. The
bel is named for Alexander Graham Bell, who was not, as one might
suppose,
American, but rather a Scot-born Canadian working in Boston. A
reference
intensity Io is defined as 10-12 wts/m2,
which
corresponds roughly to the quietest sound a normal human can
hear.
The intensity to be converted is compared to this standard, and the log
base ten is taken of the ratio. This gives the number of bels,
so
the number of decibels (dB) must be ten times more:
b = 10 log10[I/Io].
Let's try some examples:
Suppose that the sound that one professor produces (at a given
distance)
has an intensity of 10-7 wts/m2. How many
dB
does this correspond to?
Now, how many decibels would ten professors produce? What about one
hundred?
So, note that this is not a linear relationship. A multiplicative
factor
of ten in intensity is an additive increase of ten
in
decibels.
Note: we assume that we can simply add the intensities of individual
waves. This works so long as those individual waves are incoherent.
When
waves are coherent, a more difficult approach is necessary
(which we'll investigate in the second semestre). Please, no
comments
about how professors are always incoherent.
Here are the intensity levels of some common situations:
| Situation |
Intensity |
Intensity level |
| Threshold of Hearing |
10-12 W/m2 |
0 dB |
| Library Reading Room |
10-9 W/m2 |
30 dB |
| Conversation |
10-6 W/m2 |
60 dB |
| Vacuum Cleaner |
10-3 W/m2 |
90 dB |
| Rock Concert |
10-1 W/m2 |
110 dB |
| Thunder |
10 W/m2 |
130 dB |
Of course, these values depend on the distance between source and
listener.
Prolonged exposure to sounds above 90dB will cause permanent damage,
and
exposure to sounds over 110dB will be painful. Here are some
helpful
hints: ALWAYS wear ear protection in noisy situations, such as lawn
mowing
or vacuuming and on up. If you must wear headphones to listen to
music, place them just in front of your ears, not right over them.
Beats
Suppose that we have two nearly identical waves passing through a spot
in space, so that the time dependences (we'll ignore the spatial
dependence
for now) are given by:
Y1 = Ao sin(2pf1t)
Y2 = Ao sin(2p f2
t).
Using the principle of superposition, we get that total 'displacement'
from equilibrium is then the sum of these two expressions:
Ytotal = Y1 + Y2 = Ao sin(2pf1t)
+ Ao sin(2pf2
t).
Now, we'll make use of a trig identity, (which we'll prove below):
sin a + sin b = 2 sin[(a+b)/2] cos[(a-b)/2],
so that
Ytotal = 2 Ao cos(2p[(f1-
f2)/2]t)
sin(2p[(f1+
f2)/2]t).
From this we see that the frequency of oscillation is the average
of the two original frequencies, but also that the amplitude of the
oscillation
is modulated by an envelope with a frequency of | f1
- f2|/2. What will be heard, though is a
pulsing or beating in the amplitude with twice that frequency; this is
known in fact as the beat frequency:
fBeat = | f1 - f2|.
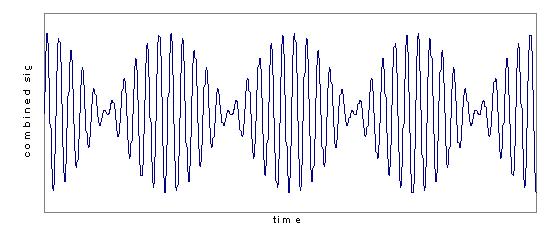
This can be (and often is) used as a method for tuning pianos and other
such instruments. Once a 'C' string is tuned to the correct
pitch,
it and the 'G' a fifth above it above are struck simultaneously.
The third harmonic of the C and the second harmonic of the G are the
same
note, and so the G string's tension is adjusted until no beats are
heard
between those two harmonics (or in other tuning schemes, a certain
number
of beats per second should be heard, but that's a whole 'nother
story...).
Doppler Effect
You're probably familiar with this effect: a car or train paasses you
while
blowing its horn, so that the pitch of the sound rises while the
vehicle
is moving toward you, but sounds lower when the vehicle is moving away
from you. We shall look at a couple of special cases, and then
integrate
the results for all such cases into a single relationship. Note,
however, that the results will only be true if there is no wind, that
is,
the medium (usually air or water) is stationary. Also, our
derivations
will be done for a one dimensional universe.
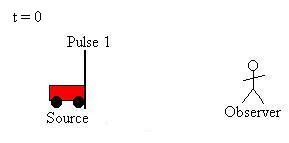
Consider a source moving at speed vSource toward (approaching)
a
stationary observer (or listener, if you insist). Instead of
having
the source emit a sinusoidal wave, let's assume that it emits pulses;
we
can later correlate these pulses to the peaks of a sinusoidal wave, if
necessary. Let the frequency of the pulse emitted by the source
be
fo,
and the time between the emission of pulses be To = 1/ fo.
Here at t = 0, the source releases a pulse, which then travels to the
right at speed vSound.
Now, let's look at the locations of everything a time t = To
later:
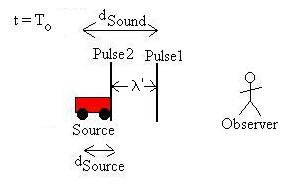
Here, at a time To later, Pulse 1 has traveled a distance
dSound = vSound To,
while the source has traveled a distance
dSource = vSource To,
at which point it emits Pulse 2.
Now, the wavelength that the observer will measure is the distance
between the two pulses:
l' = dSound -
d
Source
l' = vSound To -
vSource To.
Now we remember that, in general, f = 1/T and that
fl
=
vwave, and so this last expression can be re-written as
vSound/ f ' = vSound/fo
-
vSource/ fo,
which get re-arranged to be
f ' = f o [vSound/(vSound
- vSource)].
Now, if the source had instead been moving the other way (receding),
those
two distances would have had to have been added, changing the red
minus sign to a plus sign:
f ' = f o [vSound/(vSound
+ vSource)].
Now, suppose instead that it were the observer moving toward
(approaching)
the stationary source at speed vObserver. Once again,
let the source emit pulses at an interval of To. Let t
= 0 when Pulse 1 arrives at the observer:
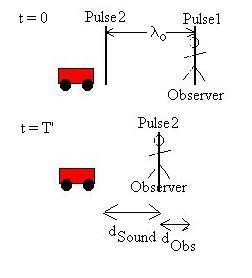
The second pulse arrives at the observer at time T', during which
interval
the pulse has traveled distance (to the right)
dSound = vSound T'
and the observer has traveled distance (to the left)
dObserver = vObserver T'.
T' is now the time between pulses, as heard by the observer.
The sum of these distances is the old wavelength, lo:
lo = dSound +
dObserver
= vSound T' + vObserver T'.
Once again remembering that, in general, f = 1/T
and that f l
= vwave,
we substiute to obtain
vSound/ f o = vSound/
f
'
+ vObserver/ f '.
This, we re-arrange to obtain
f ' = f o [vSound +
vObserver]/vSound.
Once again, if the observer had been receding from the source, there
would have been a sign reversal (blue) to
f ' = f o [vSound -
vObserver]/vSound.
Now, we can combine all these relationships, if we're careful.
First, we need to define better the terms 'approach' and 'recede.'
'Approach'
is to head in the direction of the other object, regardless of
whether
the distance between the objects is becoming smaller or not, and
'recede'
means to head in the opposite direction of the other object, whether
the
distance between is increasing or not. Then
f' = fo [vSound +/- vObserver]/[vSound
-/+ vSource],
where the upper sign is used if that object is approaching and the
lower sign if that object is receding.
What exactly would one do if there were wind?
NOTE: For light, the result is very different.
What happens if the source travels more quickly than sound?
Consider
these diagrams:
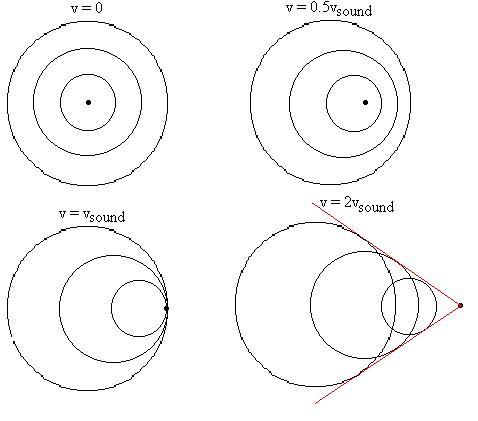
The upper left figure shows the locations of the crests of three waves
emitted by a source such as a jet while it is stationary. The
upper
right figure shows the the same when the source is moving to the right
at about 0.5 the speed of sound; note that the wavelengths will be
shorter
for listeners in the path of the source, but longer for listeners from
which the source is receding. When the source reaches the speed
of
the wave in that medium, a bow shock wave is generated; this
is
most easily seen when generated by a boat, but recent photos of jets
breaking
the 'sound barrier' have caught these shock waves as they condensed
water
vapour in the air. Once the speed of the source exceeds the speed
of the wave in that medium, the crests of all waves co-incide
to
produce a giant shock wave (red line); for jets, this results in the
familiar
sonic boom.
Some random notes:
1) The reason the Concorde was so quiet (to the passengers anyway,
not to those living on the flight path) during supersonic flight is
that
the the noise from the engines could not keep up with the cabin; one
could
hear only the noise transmitted through the body of the plane.
2) The apex angle (2q) of the cone formed
by the shockwave depends on the speed of the source:

The wave shown was generated at the instant that the source was at
its centre. In time interval t, the source moved a distance vsourcet
and
the sound moved outward a distance vsoundt.
Consider
the right triangle formed in the diagram. We see that
sinq = vsoundt/vsourcet
=
vsound/vsource.
The inverse of this ratio is referred to as the Mach number.
The
official speed record of any jet aircraft is about Mach 3, set by a
Soviet fighter. There are rumours however that the US's SR-71 has
hit Mach 5. The Space Shuttle enters earth's atmosphere at about
Mach 25.
We would like to justify the contention that
the speed of a disturbance propagates with a speed that is related to
the
natural frequency of the individual oscillators.
Consider a rectangular block of a solid, length L and
cross-sectional
area A. The material can be modelled by small balls of mass m
(representing
the atoms) connected by bonds represented by springs with stiffness k,
and relaxed length lo. We can justify this
last
statement by examining the typical potential energy curve of these
bonds:
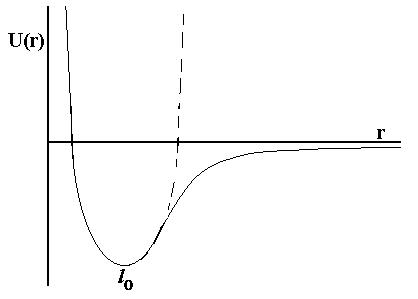
The atoms would 'like' to arrange themselves so that the potential
energy is a minimum, at r = lo. At that point,
the shape of the curve is approximately parabolic, and so the system
follows
Hooke's law,
F1 = - 2k(r-lo) = - 2k Dl,
where F1 approximately represents the x-component
of the force on one atom from two adjacent atoms (the problem
is
actually more complicated than this, even, since the amount of
stretching
or compression of any spring depends on the positions of both
of
the masses to which it's connected.). Now, we remember that the
Young's
modulus is given experimentally and macroscopically by
Y = -(F/A)/(DL/L),
where F/A is the pressure exerted on each end of the material, and
DL/L
is the resulting fractional change in length. We assert that DL/L
= Dl/lo, since we
assume
that any change of the dimensions (during equilibrium compression or
stretching
) is evenly divided among all of the bonds. Also, the pressure
F/A
is the same for the whole face of the metal as for the area
corresponding
to one atom, F1/lo2. So,
Y = -(F/A)/(DL/L) = -(F1/lo2)/(Dl/lo)
= -(F1/Dl)/lo
=
+2k/lo.
In the same way, the density can be found with the mass of one atom
and the volume that atom occupies on average:
r = m/lo3.
We know also from macroscopic experimentation that the speed of sound
in a solid is given by
v = [Y/r]1/2
So, we then show that
v = [Y/r]1/2 = [2k/lo/m/lo3]1/2
= [2]1/2 lo [k/m]1/2
So, as asserted, the speed of propagation is proportional to the
frequency
of the individual oscillators:
v ~ wo.
Does this make sense? In general, v = d/t = lo/(0.11T).
Yes,
the disturbance travels one spring length in an appreciable
fraction
of the mass's oscillation period.
Trig Identity
We want to find sin a + sin b.
Let a = [a + b]/2 and b
= [a - b]/2.
Then, a + b = (a/2 + b/2) + (a/2 -
b/2) = a
and a - b = (a/2 + b/2) - (a/2
- b/2) = b.
So, sin a = sin(a + b) = sina
cosb + sinb cosa
and
sin b = sin (a - b) = sina
cosb
- sinb cosa.
So, sin a + sin b = sina cosb
+ sinb cosa + sina
cosb
- sinb cosa = 2
sina
cosb
= 2 sin([a + b]/2) cos([a - b]/2)
Return to Notes Directory
Continue to Next Section
of Notes
D Baum 2000








