Section 1- 3 - Motion in Two Dimensions

Motion in Two Dimensions
Projectile Motion in Two Dimensions
Shape of a Projectile's Path
The Range Equation
Relative Velocity
Correlation to your Textbook

Motion in Two Dimensions

We need a new way of keeping track of the motion of a particle.  Let's define the position vector r as
r = xi + yj.
The displacement is then
Dr = rf - ro = (xf i + yf  j) - (xo i + yo j) = (xf - xo) i  + (yf - yo) j = Dx i + Dy j,
so that the displacement is the vector sum of the individual displacements in the x and y directions (no surprise there).
The average velocity is vave = Dr/Dt = [Dx i + Dy j]/Dt = [Dx/Dt] i + [Dy/Dt] j] = (vx)ave i + (vy)ave j.
The instantaneous velocity v is defined as before as lim Dt->0Dr/Dt.
The average acceleration is aave = Dv/Dt = [Dvx i + Dvy j]/Dt = [Dvx /Dt] i + [Dvy /Dt] j] = (ax)ave i + (ay)ave j.
The instantaneous velocity a is defined as before as lim Dt->0Dv/Dt.

Projectile Motion in Two Dimensions

Let's look at a common, but special, case.
We shall make three assumptions here:

This last factoid we confirmed by observing a demonstration.  First, two balls were released from rest at the same time and allowed to fall toward the table; they arrived at the same time.  Then, one ball was dropped while the other was launched horizontally from the same height at the same time; once again, they arrived at the same instant.  We concluded that the vertical motion was independent of any horizontal motion the objects may have possessed.  (In fact, there are some situations where this is not true, for example when the air flow around an object is turbulent, but we'll ignore them.)
So, we may write our kinematic equations separately for the two directions:
 

vfx = vix  + ax  t
x = xo + vix t + 1/2ax t2
vfx2 = vix2 + 2ax (x f - xi)
vx ave = [vfx + vix]/2

vfy = viy + ay  t
y = yi + viy t + 1/2ay t2
vfy2 = viy2 + 2ay (yf - yi)
vy ave = [vfy + viy]/2

The only quantity obviously common to the two systems is the time, t.

Example:
A ball is rolled horizontally off a table 1.5 m in height at 5 m/s.  How far from the base of the table will the ball strike the floor?
Draw a figure to help visualize the situation, including a system of axes with an origin (here, at the edge of the table, with y positive upward and x positive to the right):

Write down all we know:
Set yi = xi = 0.  Then, yf = -1.5 (the ball moved downward) and xf is the distance from the base we're looking for.
vix = vo cosqo = vo = 5 m/s     viy = vo sinqo = 0
ax = 0   ay = -ag = -10 m/s2
Now, choose which relationships to use; since we need the time to link the two motions, and we also need to know something about the displacements, choose
x = xi + vix t + 1/2ax t2
and
y = yi + viy t + 1/2ay t2.
Simplify the y equation and substitute in the values:
-1.5 = 0 + 0* t + 1/2(-10)t2.
t2 = (-1.5)*2/(-10) = 0.3
t = +/- 0.55 seconds - We want an answer which is in the future, so t = 0.55 s.
(Why two answers?  Once again it's a question of the equations not being very smart.  All they know is that at t = 0, the ball is at height y = 0 with a horizontal velocity of 5 m/s.  They assume that the ball got there by rising up to that point, i.e., they assume that the y-acceleration was -10 m/s2 all along.)
Substitute this result back into x equation:
x = xi + vix t + 1/2ax t2
x = 0 + 5 *0.55 + 1/2*0*t2
x = 2.7 m

Here is another example:
Take the same ball as above and launch it at at 5 m/s at a 30o angle above the horizontal.  How far from the foot of the table will it land?  Use the same origin and co-ordinate system as above.
Write down all we know:
Set yi = xi = 0.  Then, yf = -1.5 (the ball moved downward) and xf is the distance from the base we're looking for.
vix = vo cosqo = (5 m/s)*cos30o = 4.3 m/s     viy = vo sinqo = (5 m/s)*sin30o = 2.5 m/s
ax = 0   ay = -ag = -10 m/s2
As before,
x = xi + vix t + 1/2ax t2
and
y = yi + viy t + 1/2ay t2.
Simplify the y equation and substitute in the values:
-1.5 = 0 + 2.5* t + 1/2(-10)t2, or
5t2 - 2.5t - 1.5 = 0
Here, we have a quadratic equation, the solutions of which are t = -0.35 and +0.85.  We want an answer which is in the future, so t = 0.85 s.
Substitute this result back into x equation:
x = xi + vix t + 1/2ax t2
x = 0 + 4.3*0.85 + 1/2*0*t2
x = 3.7 m

Shape of a Projectile's Path

Let's try to determine the type of path a projectile will take through space near the surface of the earth.  Start once again with the kinematic equations:
x = xi + vix t + 1/2ax t2
y = yi + viy t + 1/2ay t2
Let viy = vo sinqo and vix = vo cosqo.
Also, ax = 0 and ay = ag.
Lastly, since our choice of origin is arbitrary, let's set xi = yi = 0 for simplicity.
So,
x = vo cosqo t
y = vo sinqo t + 1/2ag t2
Re-arranging the first equation gives us:
t = x / vo cosqo.
Substitute this into the y-equation:
y = vo sinqo [x /vo cosqo] + 1/2ag [x /vo cosqo]2
which simplifies to :
y = tanqo x  + 1/2ag [x /vo cosqo]2
For any given situation, qo, vo, and ag are constants, so this relationship has the form
y(x) = Ax2 + Bx
and the path is parabolic.

The Range Equation

Let's discuss a particularly special case of projectile motion which is of historical interest.  In the 17th and 18th century, being a physicist usually meant being an artillery officer.  Consider a flat plain (which is also a plane) on which are located a battery and a target.  Given an initial projection angle qo (elevation) and speed vo (muzzle velocity, for guns or cannon), how far will the projectile land from the gun (range, R)?

We'll assume, since the plane is horizontal and flat, that yo = yf = 0.
Assume that up is positive y and that the direction from cannon to target is positive x.
Also, let's say that xi = 0, xf = R, ax = 0 and ay = ag.
And, let viy = vo sinqo and vix = vo cosqo.
Then,
xf  = xi + vix t + 1/2ax t2
y = yi + viy t + 1/2ay t2
so that, after substitution,
R = vo cosqo t
0 = vo sinqo t + 1/2ag t2
Solving the second equation for t (times at which the projectile is at ground level) results in
t = 0
and
t = [2vosinqo]/(-ag)
Note that ag is presumably a negative number, so the denominator above is positive.
R = vo cosqo [2vosinqo]/(-ag)= vo2 [2sinqocosqo]/(-ag) = vo2 [sin(2qo)]/(-ag)
where we've made use of one of the trig identities.  Our result, the range equation, is then
R = vo2 sin(2qo)/|ag|,
where we've fixed any potential sign problems by taking the absolute value of ag.

Let's consider a couple of questions:
First, what angle(s) give(s) the maximum range for a given muzzle velocity?  The sine function is a maximum (1) when the angle (2qo) is 90o, so the elevation angle should be half that, or 45o, to attain maximum range.
Second, for a given range and muzzle velocity, at what angle(s) should a projectile be launched?  Re-arranging the range equation results in:
sin(2qo) = R |ag|/vo2 .
As we saw above, if R |ag|/vo2 = 1, then only 45o will do the job.  But if R |ag|/vo2 < 1, then there are two angles which will work:

What's more, those two angles will be complementary, since the curve shown is symmetric.

Example:  At what angles can a projectile be launched at 300 m/s in order to hit a target on the same level which is 5 km away?

So, what's the difference between these two paths?  At a low angle, the projectile is not in the air long, but it has a high x-component of velocity, while at a high angle, the projectile spends a lot of time in the air, but has a correspondingly lower x-component of velocity.  These two effects combine to give the same final x displacement as for the low angle case.  The first is useful in tank warfare, where it is important to hit the other guy before he gets off a shot at you, while the second is good if there are fortifications around your target.

What if R |ag|/vo2 >1?  Then there is no angle that can get the projectile to the target; it will fall short.

Just as an aside, how long are these times?  We saw above that
t = [2vosinqo]/|ag|
and so the other time is
t' = [2vosin(90o-qo)]/|ag|
t' = [2vocosqo]/|ag|

What can we say about the maximum altitude hmax attained by the projectile?
vy2 = viy2 + 2ay (y - yi)
Let yi = 0, viy = vosinqo, ay = ag, and let up be positive.
At the highest point in the trajectory, vy = 0 and y = hmax, so,
0 = [vosinqo]2 + 2ag (hmax)
hmax = [vosinqo]2/(-2ag) = [vosinqo]2/2|ag|

Relative Velocity

On occasion, it is useful to consider the motion of an object with respect to an origin/co-ordinate system which is itself in motion to some third reference frame.  The simple example given in class was that of the moving sidewalk-type 'people mover' seen at most large airports.  These conveyances allow the weary to ride from one end of the concourse to the other, while also providing those in a rush a little extra speed as they run down the walkway.  For example, consider such a walkway (W) which moves with a speed of +2 m/s with respect to the ground (G):
vW,G = +2 m/s (once again, we'll use the sign of the number to indicate the direction of the vector quantity).
The subscript notation vA,B gives the velocity of A with respect to B.
Now, think of a person (P) walking in the same direction at 1 m/s along the walkway: vP,W = +1 m/s.
It's easy to see that the person's velocity with respect to the ground is +3 m/s, since
vP,G = vP,W + vW,G.
What is the person decided to walk backward on the walkway, such that vP,W = -1 m/s?  Then, vP,G would be only +1 m/s; the person would still be going in the same direction as before, although more slowly.  If he walked at -2 m/s with respect to the walkway, he'd actually be standing still with respect to the ground, and incidently greatly annoying his fellow travelers.

Question:  Suppose that this traveler walks the correct way on the 'people mover' at a speed of 1 m/s, while his twin brother walks at 2 m/s the correct way on the return walkway.  What is the relative speed between the brothers?

Now, let's examine the relationship above more carefully:
vP,G = vP,W + vW,G.
One of the hardest aspects of relative velocity is to determine which two quantities get added to obtain the third.  Notice, though, that in the example, the lettre 'P' representing the person occupies the first subscript position in both of the terms it appears in, while the 'G' occupies the second position in both terms; only the 'W' changes position.  A quick way to remember is to add the two terms from which one subscript changes position.

Since we can add velocity vectors independently in the x, y, and z directions, we can rewrite the relationship above more generally as
vA,C = vA,B + vB,C.

Here's another example:

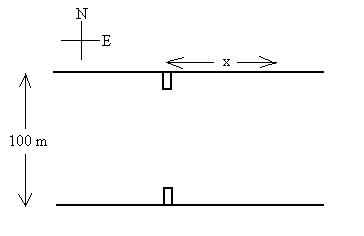
Consider a boatman who wishes to cross a river (100 metres wide) from one dock north to another exactly opposite.  His boat will make 20 m/s in calm water.  The velocity of the water is 8 m/s eastward.  He aims his boat exactly northward and sets off.  How far downstream (x) will he actually land, in what compass direction did he actually travel, and how long will it take him to get there?


We write the relative velocity relationship as
vB,G = vB,W + vW,G,  where B = 'boat,' W = 'water,' and 'G = 'ground.'

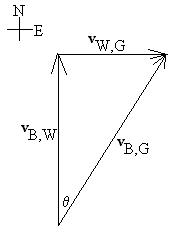
There are a number of ways to solve this; the shortest may be to realize that, if the velocity components are all constant, a displacement component diagram can be constructed,
DrB,G = DrB,W +DrW,G,
where each term is parallel to the corresponding velocity term.  The two triangles so formed are then similar, and so there is a proportionality of the lengths of the sides:

20/8 = 100/x;  x = 40m (downstream).
The direction traveled can be found using the tangent of the angle q:
tanq = 8/20; q = 21.8o.
For the time, we consider that the motion northward (in this case) is independent of the motion eastward; it wouild take 5 seconds to cover 100 metres at 20 m/s.

Now, suppose that, having learned his lesson, he tries again to cross directly to the other side.  In what direction should he aim his boat (relative to north) to arrive exactly at the other dock, and how long will it take him??


The common error here is simply to flip the triangle over.  But what should be done is to deform the triangle by sliding vW,G over until the sum, vB,G, is pointing due north:

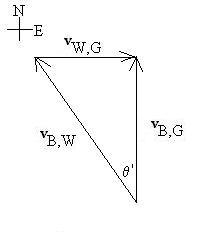
Before, the two short sides of the right triangle were vB,W and vW,G, but now those vectors are the hypotenuse and a short side, respectively.  So,
q ' = arcsin(8/20) and  |vB,G | = 20cosq '.  Finish the calculations yourself.

Mastery Question

Suppose that a man tosses a ball vertically while riding a train moving at constant velocity vT.  What shape trajectory will the man see the ball take?  What shape trajectory will someone standing by the side of the track see the ball take?
Now, suppose that the train accelerates forward (aT) and the ball is launched as before when the train has velocity vT.  What path will the observer in the train see the ball take?  What path will the stationary observer see?

Click here for solution.

Try this Applet: http://users.erols.com/renau/velocity_composition.html


Return to Notes Index
Continue to Next Section of Notes


D Baum 2000, 2001, 2002, 2017