I) Train at constant velocity:

When thrown, the ball has no initial horizontal velocity for the man in the train, so it will appear to rise and fall vertically.

The ball has initial (and constant, since a_x = 0) horizontal velocity v_T for the man on the side of the tracks.  Once launched, the acceleration is a_g, and the path is parabolic, as shown in the class notes.

II) Train accelerating:

When thrown, the ball has no initial horizontal velocity for the man in the train, but has initial (and constant, since a_x = 0) horizontal velocity v_T for the man on the side of the tracks.  For the man on the tracks, the problem is exactly the same as before; only gravity acts on the ball, so the exact same parabola is followed as before.  The only difference is that the train will in the meantime pull ahead of the ball.

Now, for the man on the train: he is accelerating forward, but to him, the ball appears to be accelerating backward, i.e., there is a pseudo-force in operation.  the equations of motion in the train man's frame will be:

x = x_o + v_oxt + ¹/₂a_xt²
y = y_o + v_oyt + ¹/₂a_yt²

for this fellow, the following values are used:  let x_o = y_o = 0, v_ox = 0, a_y = a_g, and a_x = -a_T.
x = -¹/₂a_Tt²
y = v_oyt + ¹/₂a_gt²
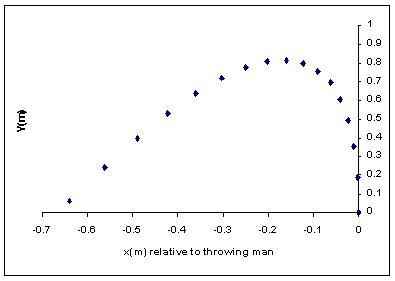
We can plot this easily on Excel.

Is this a parabola?  Certainly it's not symmetric about a vertical axis as were our other trajectories.  The usual substitution shows the path to be parabolic in the square root of x, not x.  However, what we've done is basically rotate the co-ordinate system by making the (constant) acceleration be downward and toward the rear of the train.  We should then really expect the curve to be parabolic, but about an axis tilted to the horizontal.  I'll work this out mathematically some day....