A) A = C cos q
B) A = C sin q
C) A = B + C
D) A = B - C
E) A = C - B
Please note that there is some overlap between exams. Your exams may not cover the exact material included in each of these sample exams.
Exam I - Kinematics- Solutions
Exam II - Dynamics & Statics- Solutions
Exam III - Energy & Momentum - Solutions
Exam IIII - Rotation and Rotational
Equilibrium
- Solutions
Exam V - Waves & Oscillations - Solutions
This is a closed book exam. The relations and constants on the last page may be useful; please feel free to detach it from the exam. Please answer multiple choice questions below. Show all work or otherwise justify each answer to receive full credit. IF YOU HAVE A QUESTION DURING THE EXAM, ASK IT!
SCORE:
1) Which of the following has not been the definition of the metre?
A) 1/10,000,000 of the distance between
the equator and the North Pole
B) the distance between scratches on a
platinum-iridium bar kept just outside Paris
C) the distance light travels in vacuum
in 1/299,792, 458 of a second
D) each of these has been the definition
of a metre
E) none of these has been the definition
of a metre.
2) Consider vectors A and B. If |A| = 2 and |B| = 5, then |A+B| can not be
A) 2
B) 3
C) 4
D) 5
E) 7
3) See the figure. Which of these
statements
is true?
A) A = C cos q
B) A = C sin q
C) A = B + C
D) A = B - C
E) A = C - B
4) Consider the figure, which shows an
aerial view of the path taken by an object. The object starts from rest
at I, reaching a speed vf at II. The object turns right to
III,
continues straight to IIII, then turns left to V, all at speed vf.
During
which of these intervals does the object have zero acceleration?
A) I to II
B) II to III
C) III to IIII
D) IIII to V
E) There is no interval when the
acceleration
is zero.
5) You're riding a smoothly-turning carousel of diameter 20 m which makes a complete revolution every 15 seconds. At the end of two complete revolutions,
A) your distance traveled is 63 m.
B) your displacement is 126 m.
C) your instantaneous velocity is zero.
D) your average acceleration is zero.
E) your distance traveled is zero.
Using the component method, find the magnitude and direction of vector D.
A = 13 m, qA = 25o
B = 20 m, qB = 225o
C = 7.5 m, qC = - 80o
D = A + B - C
Suppose that an airplane must fly due north a distance of 900 km in exactly two hours. All the way, the plane encounters an easterly wind (which blows to the west) of 100 km/hr. What should be the air speed of the plane, and in what direction should the pilot point the plane to arrive on schedule?
Consider a ball shot from a cannon over a flat, level plain at angle qo and with muzzle velocity vo. Neglect air resistance.
A) Show that the range is given by vo2
sin(2qo)/g.
B) Show that the maximum range is
obtained
when qo
= 45o.
HINT: sin(2q) = 2 sinq cosq
A bolt comes off an elevator that is moving upward at speed 6 m/s. The bolt reaches the bottom of the elevator shaft 3 seconds later.
A) What is the acceleration of the bolt
after it has fallen from the elevator? (2 pts)
B) How high above the bottom of the
shaft
was the elevator when the bolt came loose? (6 pts)
C) What is the speed of the bolt when
it
hits the bottom of the elevator shaft? (6 pts)
D) How long did it take the bolt to
reach
a height of 30m above the bottom of the shaft? Give a physical
interpretation
of your answer. (6 pts)
This is a closed book exam. The relations and constants on the last page may be useful; please feel free to detach it from the exam. Please answer multiple choice questions below. Show all work or otherwise justify each answer to receive full credit. IF YOU HAVE A QUESTION DURING THE EXAM, ASK IT!
SCORE:
1) A force F acts alone on a mass m, giving it an acceleration of 2 m/s2. If the same force were to act alone on a mass M (=2m), then the acceleration of M would be
A) 0 m/s2
B) 1 m/s2
C) 2 m/s2
D) 4 m/s2
E) 8 m/s2
2) Consider two automobiles traveling up I-95. The faster one travels at 33 m/s and is 150m behind the slower, which is traveling at 18 m/s. How long will it take the faster car to catch up with the slower?
A) 0.22 s B)
2.9
s C) 5.9 s D) 10
s
E) 17 s
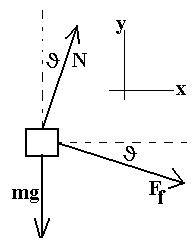
3) Consider a block of mass m which is
slid along the ceiling with acceleration a by a force F, as shown. The
coëfficient of kinetic friction between block and ceiling is
µK.
Which of the following sets of equations follow from Newton's second
law?
A) F sinq
- mg - N =
ma
F cosq -
Ff = 0 Ff
= µKN
B) F sinq
- mg - N =
0
F
cosq -
Ff = ma Ff = µKN
C) F cosq
- mg + N = 0 F sinq
- Ff = ma Ff
= µKN
D) F cosq
- mg - N = ma F sinq
- Ff = 0 Ff
= µKN
E) F sinq
- mg + N = 0 F cosq
- Ff = ma Ff
= µKN
4) Choose the answer which best completes the sentence:
If an object is at rest, then
A) no forces act on the object.
B) any forces which form third law pairs
cancel each other out.
C) the mass of the object must be very
large.
D) the sum of all forces acting on the
object must be zero.
E) the weight and the normal force must
be equal and opposite.
5) You're pushing a heavy crate across a rough floor. To do so, you must apply a force to the box. Which is the 'reaction' force to your 'action' force?
A) the floor pushing up on the box (the
normal)
B) the floor pushing backwards on the
box (friction)
C) the box pulling upward on the earth
(gravity)
D) the box pushing backwards on you
E) you pushing backwards on the floor
Consider a man in a boat who wants to
cross
a river which is 1 km wide. The speed of the boat in still water (vB,W)
is
8km/h, and the speed of the water (vW,G) is 10 km/h.
Suppose
that at first, he steers his boat at right angles to the current.
A) How far downstream will he land from
dock B? (7 pts)
B) How long will it take him to cross
(leave
answer in hours)? (5 pts)
C) Now, on his second try, he wants to land at dock B exactly opposite his starting point. At what angle should he steer his boat? (8 pts)
PROBLEM II (20 points)
Two blocks (M1 and M2)
are
on the inclines (q1
and q2),
as
shown in the figure, and are moving to the right. The string is
massless
and the wheel is frictionless, but the left-hand block/surface has
coëfficient
of kinetic friction µK.
A) Draw free body diagrams for each
mass.
Be sure to include all information, e.g., axes labels, et c.
(4
pts)
B) Write a set of equations using
Newton's second law which will allow you to determine the motion. Do
not
solve them yet. (7 pts)
C) Now, solve these equations to
find the acceleration of the masses. (6 pts)
D) Find the acceleration of the masses if there were no friction. (3 pts)
Consider a crate (M = 40 kg) which is
sitting
on a rough surface (µS = 0.3, µK =
0.2).
A force F is applied at angle q =
40o.
A) How big must F be to get the crate
just
to begin to move? (15 pts)
B) How big must F be to maintain a constant velocity, once the crate is in motion? (5 pts)
PROBLEM IIII (20 points)
A plant is hung from massless wires as
shown in the figure. What is the tension on each wire if the plant
weighs
20N? Include free body diagrams, et c.
This is a closed book exam. The relations and constants on the last page may be useful; please feel free to detach it from the exam. Please answer multiple choice questions below. Show all work or otherwise justify each answer to receive full credit. IF YOU HAVE A QUESTION DURING THE EXAM, ASK IT!
SCORE:
1) See the figure. Consider Newton's
Balls,
or the 'clackers.' Each of the balls has mass M. Assume that two of the
balls (1&2) are withdrawn to the left and allowed to collide with
the
remaining three. Just before they hit, the balls have speed vo.
Although
not all of the following outcomes do actually happen, one can be
eliminated
on the basis of momentum conservation alone. Which is it?
A) Balls 4 & 5 move to the right with
speed vo.
B) Balls 2, 3, 4, & 5 move to the
right with speed ½ vo.
C) Ball 5 move to the right with speed
2vo.
D) Balls 3, 4, & 5 move to the right
with speed ½ vo.
E) Ball 5 moves to the right with speed
3vo, while ball 1 bounces back to the left with speed vo.
2) An empty gondola car (mass = 104 kg) is moving along the tracks at 5 m/s. As it passes under a chute, the car is filled with 2x104 kg of water. What is the final speed of the car? Neglect friction.
A) zero
B) 1.67 m/s
C) 2.5 m/s
D) 5 m/s
E) 15 m/s
3) Consider the rollercoaster car shown
in the figure. The track is frictionless. If the speed of the car at
point
A is 7 m/s and h = 10m, what will be the speed at point E?
A) zero
B) 7 m/s
C) 14 m/s
D) 16 m/s
E) 250 m/s
4) Nancy Homewrecker and Tonya Thug are playing chicken on very slippery ice. If neither woman gives in and they collide, which of the systems listed below is the smallest system for which horizontal momentum is conserved ?
A) Tonya alone
B) Nancy Alone
C) Tonya and Nancy
D) Tonya, Nancy, and the ice.
E) Tonya, Nancy, the ice, and the earth.
5) Suppose that you whirl a bob of mass 0.25 kg around at the end of a string in a horizontal circle of radius 1.5 m a distance of 2 m above the floor. The tension you need to apply to the string is 73 N. How much work do you do on the bob each second?
A) 0 J (zero)
B) 4.9 J
C) 110 J
D) 688 J
E) The answer depends on how quickly you
swing the bob.
PROBLEM I (20 points)
Consider two cars which undergo a
completely
elastic head-on collision. Car 1 has mass M1 = 1500 kg and
an
initial speed of 20 m/s. Car 2 has mass M2 = 1000 kg and
initial
speed 15 m/s. Use the technique of relative velocities to determine the
velocities of each car after the collision.
A) What is the initial velocity of Car
1 in a frame in which Car 2 is initially at rest? (4 pts)
B) What is the final velocity of
Car 1 in that frame? (4 pts)
C) What is the final velocity of
Car 2 in that frame? (4 pts)
D) What is the final velocity of
Car 1 in the original frame of reference? (4 pts)
E) What is the final velocity of Car 2 in the original frame of reference? (4 pts)
Consider a mass M = 2 kg sliding across
a frictionless floor at speed vo = 8 m/s. It contacts a
spring
of constant k = 200 N/m at the same time it encounters a rough portion
of the floor with coëfficient of kinetic friction µK
= 0.15.
A) Find the distance the spring will be
compressed. (10 pts)
B) Find the final speed of the
mass
as it slides back to the left. (10 pts)
A) What is the equation definition for
kinetic energy? (4 pts)
B) Derive the Work-Energy
Theorem, Wtotal = DKE.
(12 pts)
C) Why is it necessary that the left hand side be the total work done on the object? Be specific! (4 pts)
Consider the time-varying force F(t)
shown
in the graph. This force acts (in one dimension) on a mass of 15 kg
which
is at rest at t=0.
A) What impulse has acted on the mass
during
these 12 seconds? (6 pts)
B) What is the final velocity of
the object? (8 pts)
C) How much work did the force do on
the
object? (6 pts)
This is a closed book exam. The relations and constants on the last page may be useful; please feel free to detach it from the exam. Please answer multiple choice questions below. Show all work or otherwise justify each answer to receive full credit. IF YOU HAVE A QUESTION DURING THE EXAM, ASK IT!
SCORE:
1) In class, we discussed the moments of inertia for several shapes which had the same mass M and radius, R: IHOOP = MR2, IDISC = ½ MR2, ISOLID SPHERE = 2/5 MR2. Now consider a hollow sphere of radius R and mass M. Which of the following choices places these four objects in order of increasing moment of inertia about the axes shown in the figures? HINT: use the argument given in class.
A) hollow sphere, solid sphere, disc,
hoop
B) solid sphere, hollow sphere, disc,
hoop
C) solid sphere, disc, hollow sphere,
hoop
D) solid sphere, disc, hoop, hollow sphere
E) There is no Choice E.
2) Consider a rigid body, upon which three forces act. In order for the body to be in translational equilibrium,
A) the forces must be equal in
magnitude.
B) the forces must all act in a single
plane.
C) at least two of the forces must be
equal in magnitude.
D) any two of the forces must sum to zero.
E) one of the forces must be zero.
3) Suppose that you want to remove a
rusty
nut with a wrench. You are already applying as large a force as you can
in the manner shown in the figure. To unscrew the nut, you should
A) apply the same force at point A,
perpendicular
to the handle.
B) apply the same force at point B, but
along the wrench handle.
C) apply half the force at point A,
perpendicular
to the handle.
D) apply half the force at point B,
perpendicular
to the handle.
E) get a bigger wrench.
4) Consider a tire (which rolls without
slipping) on a car traveling 10 m/s along a straight flat road. What is
the speed of the point on the outer edge of the tire shown, as measured
by a stationary observer alongside the road?
A) 0 m/s
B) 1.6 m/s
C) 10 m/s
D) 14 m/s
E) 20 m/s
5) What is the angular velocity of the second hand on the clock at the front of the room?
A) 0.105 rad/s, into the wall
B) 0.105 rad/s, out of the wall
C) 6.28 rad/s, into the wall
D) 6.28 rad/s, out of the wall
E) 6.28 rad/s, up
Consider two discs. The larger of the two has mass M and radius R, while the smaller has mass m<M and radius r<R. If the two discs are placed at the top of an incline (height h and length L), released from rest, and roll without slipping down the incline, which will reach the bottom first? Shown all work or otherwise justify your answer.
HINT: Use conservation of energy.
Consider a banked highway curve (q
=
9o) with radius of curvature r = 750m. The curve is designed
for trafic traveling at 120 km/h. Now, Daryl Dimwit takes the curve in
his 1600 kg Porsche 928S at 230 km/h (=64 m/s). If the coëfficient
of static friction between tire and road is µS = 1.1,
will Daryl make it the curve?
A) Draw a free body diagram for the car
as it rounds the curve.
B) Calculate the centripetal force necessary
to
keep the car moving in a circle around the curve.
C) Write Newton's second law for the x
and y directions, as shown in the figure above.
D) Now, solve these equations to find
the
maximum
possible centripetal force which could act on the car. Remember
that
Ff < or = µS N.
E) Will Daryl make the curve?
PROBLEM III (20 points)
A horizontal 4m long bar with weight
400
N is joined to a wall with a hinge. A 5m long wire connects the other
end
of the bar with the wall, as shown. In addition, a balloon is tied to
the
end of the bar, exerting a buoyant force of 200 N.
A) Find the tension, T, in the wire.
B) Find the vertical component of the
force
of the hinge on the bar, FV.
C) Find the horizontal component of the force of the hinge on the bar, FH.
Prove that the rotational kinetic energy of an object as it turns about some axis with angular velocity is KErot = ½ Iw2, where I (=Smi ri2) is the moment of inertia of the object about that axis.
HINT: Break the object up into many
very
small pieces.
This is a closed book exam. The relations and constants on the last page may be useful; please feel free to detach it from the exam. Please answer multiple choice questions below. Show all work or otherwise justify each answer to receive full credit. IF YOU HAVE A QUESTION DURING THE EXAM, ASK IT!
SCORE:
1) A transverse wave moving along a
compound
string goes from a region of high mass density to a region of low mass
density. Which figure best represents the orientations of the
transmitted
and reflected waves?
2) Suppose that a particular sound has an intensity level of 50 dB. If the intensity of the sound is doubled, the new intensity level will be
A) 25 dB
B) 47 dB
C) 50 dB
D) 53 dB
E) 100 dB
3) Suppose that you use a Spectrum
Analyzer
like the one in lecture to analyze the frequencies produced by an organ
pipe (see figure).
From this spectrum, you can say that
A) the pipe must be open at both ends.
B) the pipe must be closed at both ends.
C) the pipe must be open at one end, only.
D) the pipe could be either open at both
ends, or closed at both ends.
E) the pipe could be either open at one
end only, or open at both ends.
4) Suppose that you have a grandfather's clock (with pendulum) which keeps perfect time. Now you take it with you when you vacation on the moon, where gravity is only one-sixth that on the earth. If you set the clock correctly at 1:00, what time will the clock read one hour later?
A) 1:10
B) 1:25
C) 2:00
D) 3:27
E) 7:00
5) Suppose that a mass M is placed on a
frictionless surface, between two massless springs (k1 and k2),
as
shown. The springs are not actually connected to the mass, and when
the mass is at its equilibrium point, neither spring is compressed.
Find
the period of oscillation of this mass if it is set into motion.
Consider a taut string of length L, fixed at both ends. Let the tension be T and the mass be M.
A) Write an expression for the velocity
of transverse waves on this string, in terms of the given quantities.
You
do not have to derive the expression, merely write it. (4 pts)
B) Write an expression for the allowed
resonant frequencies on this string. (10 pts)
C)Write an expression for the allowed
resonant
frequencies if someone were to grab the mid-point of the string. (6 pts)
Assume that a particle is known to exhibit Simple harmonic motion, so that its position as a function of time is
where A is the amplitude and w
=
(k/m)½ is the natural frequency of the system.
A) Using Hooke's Law, prove that the acceleration as a function of time is given by
B) Using conservation of energy, prove that the velocity as a function of time is given by
Consider a human leg (still attached,
of
course!). When humans walk, the leg acts essentially like a pendulum;
this
minimizes the amount of effort the walker must expend.
A) If the period of oscillation of a leg
is actually 0.8 that of a simple pendulum of the same length, write an
expression for the period of oscillation of a leg of length L. (4 pts)
B) Estimate the length of a stride, in
terms of L, if the leg makes a maximum angle of 10o with
respect
to the vertical (both in front and behind). (4 pts)
C) Write an expression for the speed of
the walker in terms of L. (6 pts)
D) Suppose that Sarah's leg is 1 metre
long from hip to heel. At what speed would Sarah walk? (4 pts)
E) Suppose that Jesse's leg is only 0.7 metres long. How fast will Jesse walk? (2 pts)
PROBLEM IIII (20 points)
This problem was removed.This is a closed book exam. The relations and constants on the last page may be useful; please feel free to detach it from the exam. Please answer multiple choice questions below. Show all work or otherwise justify each answer to receive full credit. IF YOU HAVE A QUESTION DURING THE EXAM, ASK IT!
SCORE:
1) Which of the following statements is true?
A) Gauss' law holds true only for
symmetric
charge distributions.
B) If the net charge on a conductor is
zero, then the charge density must be zero at every point on the
surface
of the conductor.
C) If there is no charge in a region of
space, then the electric field must be zero.
D) Electric field lines never diverge
from a point in space.
E) None of the statements above is true.
2) Consider
the dipole and external electric field shown in the figure. Which
of the following statements best describes this situation?
A) The net force on the dipole is zero,
the net torque on the dipole is zero.
B) The net force on the dipole is zero,
the net torque on the dipole is not zero.
C) The net force on the dipole is not
zero, the net torque on the dipole is zero.
D) The net force on the dipole is not
zero, the net torque on the dipole is not zero.
E) There is no choice E.
3) Which of the following charges is not possible?
A) 1.6x10-19 C
B) 2.4x10-19 C
C) 3.2x10-19 C
D) 4.8x10-19 C
E) 6.4x10-19 C
4) Find the electric field magnitude at the centre of a circular ring of radius R on which charge Q is uniformly disributed.
A) zero
B) kQ/R2
C) kQ/R
D) kQ/2pR
E) kQ/pR2
5) Find the electric potential at the centre of a circular ring of radius R on which charge Q is uniformly distributed.
A) zero
B) kQ/R2
C) kQ/R
D) kQ/2pR
E) kQ/pR2
Starting
from
Gauss'
Law and showing all work, find an expression for the
electric
field at a distance r from the centres of the concentric, charged,
spherical
shells shown
A) for 0 < r < rA.
B) for rA < r < rB.
C) for rB < r < rC.
D) for r > rC.
HINT: You can do most of the work for Parts A-D all at once.
The hydrogen may be described as a positively charged (+e), stationary proton orbited by a negatively charged electron (-e). Given the radius of the circular orbit (r = 5.3x10-10 m), the mass of the electron (me = 9.11x10-31 kg), and the fact that e = 1.6x10-19 C,
A) find the force acting between electron and proton.
B) find the orbital frequency, w, of the
electron in its orbit.
C) find the speed of the electron as it moves about the proton.
Consider two infinite, flat sheets of charge (one with
charge
density s, the other -s)
which
intersect each other at a 90o
angle. Find the magnitude and direction of the electric field at
point P. You do not have to start from Gauss'Law, but can
use the results of our in-class derivation.
Describe, using words, figures, and/or equations, what happens when
a block of metal is placed in a uniform, external electric field, Eo.
Include
descriptions of the final distribution of charge within the
metal,
the mechanisms by which this state is achieved, the net E-field within
the metal, et c.
This is a closed book exam. The relations and constants on the last page may be useful; please feel free to detach it from the exam. Please answer multiple choice questions below. Show all work or otherwise justify each answer to receive full credit. IF YOU HAVE A QUESTION DURING THE EXAM, ASK IT!
SCORE:
1) Consider a parallel plate capacitor with air between the plates (kair = 1). A potiential difference Vo is applied to the plates so that the plates acquire a charge Qo. Then, with the capacitor still connected to its voltage source, a slab of dielectric material (knew = 4) is inserted. This results in a charge Qf and a potential difference Vf. Which of the following statements is true?
A) Vf = Vo and Qf < Qo
B) Vf = Vo and Qf > Qo
C) Vf = Vo and Qf = Qo
D) Vf < Vo and Qf = Qo
E) Vf > Vo and Qf = Qo
2) Consider a wire with length Lo and cross-sectional area Ao, made of a metal of resistivity r, which then has a resistance Ro. If the wire were to be extruded out to three times its original length, what would be its new resistance?
A) Ro/9
B) Ro/3
C) Ro
D) 3Ro
E) 9Ro
3) Suppose that a parallel plate capacitor has capacitance Co. Suppose that we insert a third plate exactly between and parallel to the other two. Then, the new capacitnace will be
A) Co/4
B) Co/2
C) Co
D) 2Co
E) 4 Co
4) Which of the following relationships is applicable to the circuit
shown?
A) - R1I1 + R2I2 = E1
+ E2
B) - R1I1 - R2I2 = E1
+ E2
C) R1I1 + R2I2
= - E1 + E2
D) R1I1 + R2I2
= E1 + E2
E) - R1I1 + R2I2 = E1
- E2
5) Consider
the circuit at right. What fraction of the total current ITOT
will pass through the 30 W resistor?
A) 1/4 ITOT
B) 1/3 ITOT
C) 1/2 ITOT
D) 2/3 ITOT
E) 3/4 ITOT
Using any means you see fit (e.g., words, graphs, formulas,
diagrams,
et
c), prove that the energy stored in a capacitor is given by U = 1/2QV.
PROBLEM II (20 points)
Consider a pair of parallel plates (like a capacitor), each of area 1 m2 and separated by 1 cm, which are charged up so that there is a potential difference of 5000 V between them. A proton (mass = 1.67x10-27 kg, charge = 1.6x10-19 C) is placed at rest next to the positely charged plate.
A) What is the electric field between the plates? (4 pts)
B) What is the electric force acting on the proton? (4 pts)
C) The proton will move toward the negatively charged plate. Find the change in its potential energy as it moves from one plate to the other. (4 pts)
D) Find the proton's kinetic energy just before it hits the negative plate. (4 pts)
E) Find the proton's velocity just before it hits the negative plate. (4 pts)
A) Prove that three resistors (R1, R2, & R3) in series are equivalent to a single resistor, Req, where Req = R1 + R2 + R3. (10 pts)
B) Prove that three resistors (R1, R2, & R3)
in
parallel are equivalent to a single resistor, Req, where
1/Req = 1/R1 + 1/R2 + 1/R3.
(10
pts)
PROBLEM IIII (20 points)
A fuse is a device composed of a thin band of metal whose purpose is to protect your home from fire. Typically, a current of more than 20 A through a fuse causes it to melt. Explain how you can arrange to have more than 20 A pass through the fuse, why this is a fire hazard, and how the fuse acts to protect your home.
This is a closed book exam. The relations and constants on the last page may be useful; please feel free to detach it from the exam. Please answer multiple choice questions below. Show all work or otherwise justify each answer to receive full credit. IF YOU HAVE A QUESTION DURING THE EXAM, ASK IT!
SCORE:
1)
Consider
the three currents, +I, -I, and +i, as shown in the diagram. In which
of
the following directions will the force on +i act?
A) in the +x direction
B) in the -x direction
C) in the +y direction
D) in the -y direction
E) There will be no net force on +i.
2)
Consider
an infinitely long wire with a circular loop as shown. The loop
has
radius 2 cm and the wire carries 7 amps. What is the magnitude of
the magnetic field at the centre of the loop?
A) zero
B) 7x10-5 T
C) 1.5x10-4 T
D) 2.2x10-4 T
E) 2.9x10-4 T
3) Consider the figure, in which there is a magnetic field (out of the page). Three particles enter the region and follow paths as shown. Which of the following statements is true?
A) X is positive, Y is negative, Z is neutral (no charge)
B) X is negative, Y is positive, Z is neutral
C) X is positive, Y is positive, Z is positive
D) X is negative, Y is negative, Z is neutral
E) X is positive, Y is positive, Z is negative
4)
Consider a
current-carrying circular loop in a magnetic field, as shown.
Which
of the following figures shows correctly the orientation of the loop's
magnetic moment (µ) and the torque acting on the loop (t)?
5) Two circular hoops (radius R) are parallel, co-axial, almost in
contact
with one another (separation d) , and carry equal currents (I) in
opposite
directions. How much force does the upper loop exert on the lower
loop? HINT: Think about what one loop looks like to a bug perched
on the other loop.
A) moI2R/d
B) 2pmoIR/d
C) moI2R/2pd
D) moI/2pd
E) 2moI2R/d
Consider a mass spectrometer. Particles are ionized (charged) and shot through a velocity selector, a region of crossed electric and magnetic fields. The selected particles then encounter a magnetic field which bends the trajectory into a semi-circle. The radius of this path is measured with a detector.
A) What will be the velocity of the particles which pass through the velocity selector undeflected if E = 5000 V/m and B = 0.1 T? (7 pts)
B) If the radius of the curved trajectory were 1.6 cm, which of the
choices listed below are these particles most likely to be?
Assume
B is still 0.1 T. (13 pts)
| PARTICLE | CONFIG. | CHARGE | MASS | Q/M Ratio |
| Neutron |
|
|
|
|
| Proton |
|
|
|
|
| Deuterium |
|
|
|
|
| Tritium |
|
|
|
|
| Helium-3 |
|
|
|
|
| Helium-4 |
|
|
|
|
Consider
the
arrangement
of conductors shown in the figure. At the centre is
an
extremely thin, infinitely long wire carrying current I1.
An
infinitely long, extremely thin shell is concentric with the wire,
has
radius R, and carries current I2 (<I1).
Starting from either the Biot-Savart Law or Ampere's Law, which
ever
you think is more appropriate, find the magnetic field, including
direction,
for
A) r < R. (10 pts)
B) r > R. (10 pts)
HINT: You can do most of parts A & B together.
You're stranded on a planet where there is no test equipment or
minerals
around. The planet does not have any magnetic field. An
alien
hands you two pieces of iron, one of which is a magnet and the other of
which is not; otherwise, they're identical. How can you tell
which
is the magnet? You may not use any method which will destroy the
magnet.
Consider the material shown below. The orientations of the
magnetic
moments of the atoms are given by the arrows (point = N, tail
=S).
There is no external magnetic field in the vicinity of the
material.
Answer the following questions as completely as you can.
A) The magnetic moments of these atoms appear to exhibit what type
of ordering? Explain.
B) Is this piece of material a magnet? Explain why or why not.
C) How could one destroy this ordering of the magnetic moments? Why would that succeed?
D) What is a magnetic domain?
E) Draw in lines between the domains in the diagram above.
This is a closed book exam. The relations and constants on the last page may be useful; please feel free to detach it from the exam. Please answer multiple choice questions below. Show all work or otherwise justify each answer to receive full credit. IF YOU HAVE A QUESTION DURING THE EXAM, ASK IT!
SCORE:
1) An ideal (no losses) step-down transformer at the end of a transmisison line reduces the effective voltage from 2400 V to 120 V. The average power output of the transformer is 5000 W. The primary coil has 10,000 turns. What is the average power input to the transformer?
A) 0.5 W
B) 250 W
C) 5000 W
D) 100,000 W
E) 1,000,000 W
2)
Consider
an infinitely long straight wire carrying current Io laid
across
along a diameter of a loop of wire of radius R . If the current
in
the wire is reduced from Io to 0 in time to
seconds,
then what is the magnitude of the average induced emf in the
loop?
A) IopR2/to
B) moIoR/2to
C) moIopR/2to
D) moIoR2/to
E) zero (no emf is produced)
3) Suppose that you're given a black box which contains a
series
combination of either LR, LC, RC, or LRC components. If at f =
400
Hz, E lags the current by 27o,
then
what's in the box?
A) RC
B) LC
C) LR
D) LRC
E) Either RC or LRC, there is not enough information to tell which.
4) Inductance is measured in Henrys, while capacitance is measured in Farads. What are the SI units of LC?
A) ohms
B) ohms-1
C) seconds
D) seconds2
E) seconds-1
5) What is Imax provided by the power supply if the
frequency
is extremely low?
A) 0 (zero)
B) 0.2 amps
C) 0.3 amps
D) 0.6 amps
E) "infinite"
A helicopter has blades of length 9 m which turn at a frequency of 5 revolutions per second. If the vertical component of the earth's magnetic field is 3x10-5 T, what emf is generated between the hub of the rotor and the ends of each blade?
Hint: How much area do the blades sweep out each
second?
Consider the circuit shown below. The switch was thrown long
ago
to include the battery in the circuit. Now, however, at time t =
0, we change the switch to the other position, as shown. Let E
= 6 V, R = 20 W, and L = 30 mH.
A) Write Kirchhoff's Loop Law (using symbols) for the circuit as
shown.
DO NOT SOLVE. (4 pts)
B) At time t = 0, the instant after the switch is changed, what is the potential drop across the inductor? (2 pts)
C) At time t = 0, the instant after the switch is changed, what is the current in the circuit? (2 pts)
D) Write the solution for I(t>0) for the equation in part A. Include numerical values. (4 pts)
E) How much time is required for the current to fall to one-half of the initial value (given in part C)? (8 pts)
Starting with Faraday's Law of Induction, E = (-)NDFM/Dt, and comparing to E = (-)L DI/Dt, find the self inductance of a toroid of radius R and coil radius r. Assume that R >> r.
Consider a series LRC circuit for which L = 0.01H, C = 2x10-6 F, R = 4 W , and Emax = 40V.
A) Find the resonant (natural) frequency. (4 pts)
B) Find the impedance at f = 2000 Hz. (6 pts)
C) Find Imax at f = 2000 Hz. (2 pts)
D) Find VR, the maximum voltage across the resistor. (4 pts)
E) Find the phase angle between the applied emf and the current. (4 pts)
This is a closed book exam. The relations and constants on the last page may be useful; please feel free to detach it from the exam. Please answer multiple choice questions below. Show all work or otherwise justify each answer to receive full credit. IF YOU HAVE A QUESTION DURING THE EXAM, ASK IT!
SCORE:
1) Often, prisms, rather than mirrors, will be used to 'reflect' light by using the phenomenon of total internal reflection (see figure). If the glass prism is submerged in water (nW = 1.33), what is the minimum index of refraction of the glass necessary for total internal reflection to occur for the situation shown?
A) 0.94
B) 1.00001
C) 1.33
D) 1.41
E) 1.88
2) A horizontal ray of light is incident on a vertical flat mirror at an angle of 23o. If we rotate the mirror about a vertical axis by 17o, while keeping the incident ray fixed, by what angle shall we rotate the reflected ray?
A) 0o
B) 17o
C) 23o
D) 34o
E) 46o
3) One has a concave spherical mirror with a focal length of +0.25 m. An object placed in front of this mirror produces an image which has a magnification of -8. What is the object distance?
A) 0.03 m
B) 0.22 m
C) 0.28 m
D) 2 m
E) 4 m
4)
Suppose that
you have three ideal polarizers, as shown in the figure. The
orientation
of the transmission axes of each of the three sheets is labeled
relative
to the vertical. A beam of unpolarized light with intensity Io
is incident on the first sheet. Calculate the intensity of the
light
transmitted through the third sheet if q1
=
60o, q2 = 40o,
and
q3 = 60o.
A) 0.125Io
B) 0.15Io
C) 0.23Io
D) 0.39Io
E) 0.44Io
5) Suppose that two loudspeakers are placed side by side a distance d apart in a large grassy field where sound is not strongly reflected from the ground. They each produce sound with wavelength l. If the speakers are 180o out of phase with one another, then which of the expressions below describes the angles at which no sound can be heard, measured with respect to the perpendicular bisector of the line joining the two speakers?
A) d sinq = (m+1/2)l
m = 0, ±1, ±2...
B) d sinq = (m+1/2)l
m = ±1, ±2, ±3...
C) d sinq = ml
m
= 0, ±1, ±2...
D) d cosq = ml
m
= 0, ±1, ±2...
E) d cosq = (m+1/2)l
m = ±1, ±2, ±3...
Consider a series of layers of transparent materials arranged as
shown
in the figure. The interfaces between layers are all horizontal
and
parallel and the indices of refraction for each are given. If a
light
ray is incident from air onto the first layer with an angle
measured
from the normal of 11.2o, what will be the angle at which
the
ray exits the stack back into air? Let n1 = 1.0, n2
= 1.3, n3 = 1.1, n4 = 1.25, and n5 =
2.2.
The BTSC standard 20" colour television picture comprises 512 horizontal lines and is 0.33 m high.
A) What is the vertical distance between adjacent lines? (4 pts)
B) What are the two extreme values of the wavelengths visible to humans? (6 pts)
C) If a typical diameter of the pupil of a human eye is 3 mm, what is the minimum distance one should sit from the TV screen? (10 pts)
Below is shown a mirror with radius of curvature R = 12 cm (centre
of
curvature is marked with a black dot), along with its (perpendicular)
optical
axis. Also shown is an object.
Note: Even though the mirror is drawn flat to aid in ray
tracing,
it is curved. Also, the figure is not to scale.
A) Is the mirror concave or convex? Explain briefly. (4
pts)
B) Indicate the position of the focal point. (2 pts)
Determine the answers to the questions below, using raytracing. Use a straightedge!
C) Trace at least three rays to determine the position of the image. (2+2+2 pts)
D) What is the image distance? Show on the diagram. (2 pts)
E) Is the image inverted or erect? Explain briefly. (2 pts)
F) What is the magnification of the image? Show work. (2 pts)
G) Is the image real or virtual? Explain briefly. (2
pts)
PROBLEM IIII (20 points)
Fill in the chart below. Each column represents a different mirror. All distances are in cm. Be certain to include negative signs, where appropriate. There are three boxes which need not be filled in.
NO PARTIAL CREDIT CAN BE GIVEN!!!
| Type (Plane, Convex, Concave) |
|
|||
| Focal Length |
|
|||
| Radius of Curvature |
|
|
||
| Object Distance |
|
|
||
| Image Distance |
|
|
|
|
| Image (Real/Virtual) | ||||
| Image (Upright/Inverted) | ||||
| Magnification |
|
|
|
This is a closed book exam. The relations and constants on the last page may be useful; please feel free to detach it from the exam. Please answer multiple choice questions below. Show all work or otherwise justify each answer to receive full credit. IF YOU HAVE A QUESTION DURING THE EXAM, ASK IT!
SCORE:
1) Engine A, which operates on the Carnot cycle, takes QH = 300 cal and produces W = 200 J each second. Engine B, which operates on the Loh cycle, takes QH = 600 cal and produces W = 500 J each second. Which of the following statements is true?
A) A has a higher thermodynamic efficiency than does B.
B) B has a higher thermodynamic efficiency than does A.
C) A and B have the same thermodynamic efficiencies.
D) It is impossible to tell which has the higher thermodynamic
efficiency.
E) A exhausts more thermal energy QC than does B.
2)
Consider the
gas molecule for which a model is shown in the figure. According
to the Equi-partition of Energy Theorem, the molar heat capacity Cv
of this material should be
A) 1.5 R
B) 2.5 R
C) 3 R
D) 3.5 R
E) 4.5 R
3) The headline on next month's Physics Today reads 'Man invents engine which turns heat directly and completely into work.' Such an engine would
A) violate the First Law but be consistent with the Scond Law.
B) violate the Second Law but be consistent with the First Law.
C) violate both the First and Second Laws.
D) be consistent with both the First and Second Laws.
E) There is no Choice E.
4) Two
moles
of an ideal gas goes through the cycle shown, part of which is irreversible.
The
change in the entropy of the gas for the cycle is
A) 5x105 J/K
B) 3x105 J/K
C) 2x105 J/K
D) 1x105 J/K
E) 0 J/K
5) Consider a gas which undergoes an isothermal process whereby the pressure is tripled (Pf = 3Po). Correspondingly, the final volume is
A) Vf = 9 Vo
B) Vf = 3 Vo
C) Vf = Vo
D) Vf = Vo/3
E) Vf = Vo/9
A 200 kg block of ice at 0oC is placed in a large lake. The temperature of the lake is just slightly higher than 0oC, and so the ice melts.
A) Do you expect the entropy of the universe to increase, decrease, or remain the same? Justify briefly your answer. (4 pts)
B) What is the entropy change of the ice? (4 pts)
C) What is the entropy change of the lake? (4 pts)
D) What is the entropy change of the universe, according to these calculations? (4 pts)
E) Account for any disagreement in the answers to Parts A and D.
Consider
an
engine
which runs on the cycle shown in the figure. Assume that the
working
fluid is a diatomic gas in which molecules rotate, but do not vibrate.
A) Find the work done by the gas in the cycle. (8 pts)
B) Find the heat into the gas in each step of the cycle (some terms may be negative). (8 pts)
C) Find the thermodynamic efficiency of this engine. (4 pts)
Consider an ideal gas at temperature T1 in a closed container.
A) Sketch a diagram showing the approximate probability of any
molecule
having a given speed. (5 pts)
B) Explain qualitatively why the curve has this shape. (5 pts)
C) Draw a similar curve if the temperature of the gas is raised to T2
>T1. (5 pts)
D) Explain qualitatively any differences in the shapes of the
curves.
(5 pts)
Given that, for a process at constant volume,
MC1 - Each of these has been a definition of a metre. (D)
MC2 - The maximum value of |A+B|
will
be when they point in the same direction (2+5=7). The minimum
value
will be when they point in opposite directions (|2-5|=3). So, 2 is not
possible. (A)
MC3 - Since A + C = B,
the
only correct answer is (D), A = B - C.
Answer A is incorrect, since it implies that A and C
are
in the same direction.
MC4 - (C) In all other intervals, there is a change in either the magnitude or the direction of the velocity.
MC5 - Check each quantity - distance = 2x circumference = 128m - displacement = 0 (you end where you start) - instantaneous velocity = 63m/15 sec = 4.2 m/s - ave acceleration = (vf - vo)/Dt = 0 since vf = vo so correct answer is (D)
PROBLEM I
In general, Ax = A cosq and Ay = A sinq. So,
Ax = 13 cos25o =
11.78m
Bx = 20 cos225o
= -14.14m
Cx = 7.5 cos(-80o)
=
1.30m
Dx =Ax + Bx
- Cx = (11.78) + (-14.14) - (1.30) = -3.66 m
Ay = 13 sin25o =
5.5m
By = 20 sin225o
= -14.14m
Cy = 7.5 sin(-80o)
=
-7.4m
Dy = Ay + By
- Cy = (5.5) + (-14.14) - (-7.4) = -1.25 m
Then, D = (Dx2 + Dy2)½ = 3.86 m and = arctan(Dy /Dx) = arctan(-1.24/-3.66) = 18.7o However, we check the signs of the components and discover that the signs are incompatible with this answer. We need to add 180o to obtain the correct answer of 198.7o.
Use the notation, vp,g
to represent the velocity of the plane wrt the ground, et c.
We know that vp,g =
900 km/ 2 hrs = 450 km/h North and that vw,g = 100
km/h
West.
We also know that vp,g
= vp,w + vw,g , therefor,
vp,w = vp,g
- vw,g = 450 N - 100 W = 450 N + 100 E
Then |vp,w| = (4502
+ 1002)½ = 460 km/h
Direction is arctan(450/100) = 77.5o
N of E where I have treated East as the x direction and North as
the
y direction.
A) R = xo + voxt (since ax = 0, & let xo=0) y = yo + voyt + ½ ayt2 (For complete trip, y = yo = 0, and of course, ay = ag = -g)
Solve second Eq for t: 0 = voyt - ½ gt2 => t = 0 or t = 2 voy /g
Substitute this second solution into the x equation:
R = vox (2 voy /g) = (2/g) vox voy = (2/g) (vo cosqo) (vo sinqo) = (vo2/g) (2 sinqocosqo) = (vo2/g)(sin 2qo)
B) R goes as sin 2qo. R will be a maximum when sine is a maximum, which will occur when 2qo = 90o, which will happen when qo is 45o.
A) ay =ag = -9.8 m/s2, obviously due to gravity alone.
B) y = yo + voyt
+ ½ayt2 But yf
= 0 at bottom of the shaft, voy = +6 m/s, ay =
-9.8
m/s2, and t = 3 sec.
So, yo = yf - voyt
-
½ayt2 = 0 - 6(3) - ½(-9.8)32
= 27 m
C) v = vo + at = 6 +(-9.8)3 = -24 m/s where (-) means downward.
D) y = yo + voyt
+ ½ayt2
solve
for t when y = 30.
30 = 27 + 6t + ½(-9.8)t2
=>
5t2 - 6t + 3 = 0 (quadratic eq)
t = (- -6 ± (36 - 4(5)3)½)/(2×5)
=
0.4 ± 0.49i
Answer
is not real => bolt never reaches 30 m!
MC1) F = ma. If F is constant, then doubling m halves a, so a = 1 m/s2 (B)
MC2) Use relative velocities vRel = 33-18 = 15 m/s. At 15m/s, it will take the faster car 10 seconds to cover the 150m between the cars. (D)
MC3) See figure. Note that the normal
force
is down. Fsinq
- mg -N = 0 Fcosq
- Ff = ma Ff = µKN
(B)
MC4) Correct answer is (D).
F
= ma. Consider the other answers:
A- see D. There can be forces on the
object,
but they must cancel.
B- third law pairs never cancel each
other,
even though equal and opposite, since they act on different objects.
C- nonsense answer
E- Not necessarily true, see MC2!
MC5) If A acts on B, then B acts on A. (D)
A) Two solutions: first, use similarity
of the displacement and velocity vector triangles (see figure) to write
that 10/8 = x/1 so x = 1.25 km. OR, do part B first and see
that
the time to cross is 0.125 hrs. Then, since the velocity component
downstream
is simply the speed of the water, d = vW,G*t = 10*0.125 = 1.25
km.
B) To find the time to cross, only the
transverse speed matters: t = d/v = 1 km / 8 km/h = 0.125 hr
C) Redraw the velocity vectors as shown
in the figure. He can never cross the river this way. Even if he heads
directly upstream, he will float downstream at 2 km/h. OR, find the
angle
such that sinq =
vW,G/vB,W = 10/8 = 1.25, and there is no such
angle.
A) see figures
B) T
-
Ff - m1gsinq1
= m1a (1)
N1 - m1gcosq1
= 0 (2)
Ff - µKN1
= 0 (3)
m2gsinq2
- T = m2a (4)
N2 - m2gcosq2
= 0 (5)
C) Substitute (2) & (3) into (1) to
obtain: T - µK(m1gcosq1)
- m1gsinq1
= m1a
Then, add (4) to eliminate the Ts:m2gsinq2
- µKm1gcosq1
- m1gsinq1
= (m1 + m2)a
Therefor, a = g [m2sinq2
- µKm1cosq1
- m1sinq1]/[m1
+ m2]
D) take the answer to Part C, but let µ = 0. a = g [m2sinq2 - m1sinq1]/[m1 + m2]
See figure.
F sinq
+ N - Mg = 0
F cosq
-Ff = Ma = 0 (not moving yet, so a = 0)
Ff = µSN (just
about to move, so use equality)
So, F cosq
= Ff = µSN = µS(Mg - F sinq)
=> F(cosq
+ µS F sinq) = F(cosq
+ µS sinq)
= µSMg => F = µSMg / [cos q+
µS sinq]
F = 0.3*40*9.8/[0.77 + 0.3*.68] = 122
N
B) Use result of part A, but replace
µS
with µK
F = 0.2*40*9.8/[0.77 + 0.2*.68] = 87
N
See figure. Clearly, T3 is
20N,
since it must support the weight of the plant. We could justify this
with
another free-body diagram of the plant and use of the third law.
y: T2sin53o + T1sin30o
- T3 = 0
x: T2cos53o - T1cos
30o = 0
Easiest to substitute x eq into the y
eq:
T2 = T1cos30o/cos53o
[T1cos30o/cos53o]*sin53o
+ T1sin30o = T3 = 20 => T1[1.65]
=
20 => T1 = 20/1.65 = 12.1 N
T2 = 12.1[cos30o/cos53o]
=
17.5N
MC1 - Look for one scenario for which p
is not conserved. (D)
po = mvo + mvo
= 2 mvo pf
= m(½ vo) + m(½ vo) + m(½ vo)
=
3/2 mvo
MC2 - po = 104*5 = 5x104 kg m/s pf = (104 + 2x104)*vf = 3x104 vf => vf = 5x104/3x104 = 1.67 m/s (B)
MC3 - KEo + PEo = KEf => ½ m 72 + m*9.8*10 = ½ mvf2 => 24.5 + 98 = 0.5 vf2 => vf = 15.6 m/s (D)
MC4 - Tonya & Nancy (C)
MC5 - W = 0 since tension is perpendicular to the displacement at any instant. (A)
Use the chart system discussed in class.
| initial frame | convert | new frame | new frame | convert back | initial frame |
| v10 = +20 | add 15 | v10' = +35 | v1f' = +7 | subtract 15 | v1f = -8 |
| v20 = -15 | add 15 | v20' = 0 | v2f' = +42 | subtract 15 | v2f = +27 |
A) In order to make v2o = 0, we must add 15 m/s to each car's velocity, so v1o' = 20 + 15 = 35 m/s.
B) Use the relationships given: v1f' = v1o'*[m1-m2]/[m1+m2] = 35*[1500-1000]/[1500+1000] = 7 m/s
C) v2f' = v1o'*2m1/[m1+m2] = 35*2*1500/[1500+1000] = 42 m/s
D) Now we need to revert to the
original
frame, so subtract 15 m/s from each of the final velocities found above.
v1f = 7 - 15 = -8 m/s
E) v2f = 42 - 15 = 27 m/s
A)
The frictional force is obtained using
NII for the vertical direction: N - mg = may = 0.
Then,
Ff = µKN = µKmg.
Consider teh two points: the mass is
moving
to the right and the spring is relaxed, and the mass is at rest with
the
spring compressed a distance xf.
Wfriction = DKE
+ DPEspring
= ½ mvf2 - ½ mvo2
+ ½ kxf2 - ½ kxo2
= - ½ mvo2 + ½ kxf2
but also equals more directly Ff*d*cos180o
= -µKmgxf.
So, -µKmgxf
= - ½ mvo2 + ½ kxf2
=>
½ kxf2 +
µKmgxf
- ½ mvo2 = 0 (quadratic eq)
plug in numbers: 100 xf2
+ 2.94xf - 64 =0 We assume that xf
>0 so take the positive root: xf = 0.785m
B)
Now consider teh two points: the mass
initially moving to the right and the spring relaxed, and the mass
moving
(finally) to the left with the spring relaxed (DPE
= 0 in this case).
½ mvf2 -
½ mvo2 = 2(-µKmgxf)
The
two is there because the mass makes two passes over the rough
region.
vf2 = vo2
-4µgxf = 59.4
=>
vf = 7.7 m/s
A) KE = ½ mv2
B)
Use the convention such that the sign
of each vector reflects its direction:
Wtotal = SWi
= S(FiDx)
= (SFi)
Dx
= FtotalDx
= (ma)
Dx
= m (a
Dx)
Since we know that vf2
= vo2 + 2aDx,
we can write that a Dx
= (vf2 - vo2)/2.
Then,
Wtotal = m
(a Dx)
=
m (vf2 - vo2)/2 = ½
mvf2 - ½ mvo2
Define the KE as ½ mv2.
Then
= KEf - KEo
=
DKE.
C) It is essential that this be the total work, since that requires us to use the total force, and only by using the total force can we invoke Newton's second law and substitute ma.
A) J = FDt = area under curve = ½ (10+30)*3 + 30*5 + ½ 30*2 - ½ 30*2 = 210 kg m/s
B) J = Dp = mvf - mvo but vo = 0, so vf = J/m = 210/15 = 14 m/s
C) W = ½ mvf2 - ½ mvo2 = ½ 15*142 = 1470 J
MC1 - The method used in class compared the distributions of mass within each of the objects. The farther from the axis the mass is, the higher the moment of inertia. The hollow sphere has more mass near the centre than does the hoop, so IHS<IH. The hollow sphere has less mass near the centre than does the solid sphere, so IHS>ISS. If we flatten the hollow sphere into a pancake, we see that there is more mass at the edges than for the disc, so IHS>ID. Therefor, the order is given by (C).
MC2 - To be in equilibrium, Ftot
=0
=> F 1 + F 2 + F3
= 0 => F3
=
- (F 1 + F 2)
i.e, F 3 is in the
plane
of F 1 & F 2. (B)
MC3 - t = rFsinq. F is as big as possible, sinq is as big as possible, need to increase r. (E)
MC4 - If vtire = 10 m/s,
then
vtangential as seen from the frame of the tire is 10 m/s. So
for point P, add the tangential velocity and the translational velocity
as shown to obtain a speed of (102+102)½
= 14 m/s (D)
MC5 - w =
#rad/sec = 2/60 = 0.105 rad/sec. Use RHR for direction - into the wall
(A)
The one with the higher velocity at the
bottom (vF) has the higher average velocity, and therefor
the
quickest time to arrive at the bottom.
Use conservation of energy: mgh + 0 =
½ mvf2 + ½ Iwf2
But, I = ½ mr2 for a
disk and w=v/r
if there's no slipping. Substitute.
mgh = ½ mvf2
+ ½ (½ mr2)(vf2/r2)
Simplify.
mgh = 3/4 mvf2
=>
vf = (4gh/3)½
Since the final speed is independent of
both the masses and the radiuses of the disks, they arrive at the
same
time!
A) See figure.
B) FC = mv2/r = 1600*642/750 = 8738N
C)Use NII: y: -mg +Ncosq - Ffsinq = 0 x: Nsinq +Ffcosq = may =maC = mv2/r Ff <µSN (not equal)
D) Now to find the maximum
possible
centripetal force, we assume that the frictional force is maxed out at
Ff = µSN. Substitute these eqs:
Nsinq
+ Ff cosq
= FCmax
=> Nsinq
+ µSN cosq
= FCmax
=> N[sinq
+ µS cosq]
= Fcmax
From the y-equation: Ncosq
= Ffsinq
+ mg = µSNsinq
+ mg Solve for N.
N[cosq
- µSsinq]
= mg => N = mg/[cosq
- µSsinq]
Substitute into the x-equation.
Fcmax = N[sin q
+
µS cosq]
= {mg/[cosq
- µSsinq]}*[sinq
+ µS cosq]
= 1600*9.8*(1.24/0.81) = 23,838N
E) He will easily make the curve.
A) Place the pivot point at the hinge
to
eliminate as much calculation as possible. Let L = the length of the
bar.
The angle q = arccos
(4/5) = 37o .
S t = FV*0
+
FH*0 + BL + TLsinq
-wL/2 = 0
Then T = [wL/2 - BL]/Lsinq
= [400*4* ½ - 200*4]/ 4*0.6 = 0 (purely a coincidence!)
B) SFy = FV - w + B + Tsinq = 0 => FV = w - B - Tsinq = - 400 - 200 - 0 = 200 N
C) S Fx = FH - Tcosq = 0 => FH = 0
KEtotal = SKEi
(for all the tiny little masses mi )=
S
½ mi vi 2 = S
½ mi (wi
ri)2
but since the object rotates as a rigid
body, all of the ws
are the same.
= (S
½ mi ri2)w
2
= ½ (Smi
ri2) w2
= ½ (S
Ii ) w2
= ½ Itot w2
Q.E.D.
MC1 - The transmitted wave is always in the same orientation as the incident wave. If we're going from high Z to low Z, there is no inversion upon reflection, so (B) is correct.
MC2 - The new sound must be louder, so (A), (B), & (C) are out. Since the intensity only doubled, and we know that the decibel scale is logarithmic, the new intensity level should be only a little higher than the original. (D)
MC3 - Since only odd multiples of the fundamental appear, the pipe is closed at one end only. (C)
MC4 - T = 2p(L/g)1/2. If gmoon is 1/6 gearth, then Tmoon = 61/2 Tearth. OR, the clock runs 2.45 times more slowly on the moon than it does on the earth. So one hour would show up as 1hr/2.45 = 0.41 hr = 24.5 minutes on the clock. So, the clock would read 1:25 (B)
MC5 - The period due to spring 1 would be T1 = 2p(M/k1)½. The period due to spring 2 would be T2 = 2p(M/k2)½. But each spring acts on the mass through only half a cycle, so Ttotal = ½ T1 + ½ T2 = p(M/k1)1/2 + p(M/k2)1/2. (E)
A) v = (T/µ)1/2 = (TL/M)1/2
B) Fixed at each
end
=> node at each end => fn
= nv/2L
n = 1, 2, 3, ...
C) If someone grabs the mid-point, only
frequencies which have a node there will survive: f'n =
nv/2L
n = 2, 4, 6, ...
A) Write Newton's second law: SF = ma => -kx = ma => a = -(k/m)x = -(k/m)Asin(wt) = -w2Asin(wt).
B) Consider that point at which the
spring
has reached maximum extension (x = A) and the block is at rest. Then
the
total energy is ½ kA2. When the block is at some
other
position, the total energy is ½ mv2 + ½ kx2.
So,
½ kA2 = ½ mv2
+ ½ kx2
mv2 = kA2 - kx2
= k (A2 - x2)
v = (k/m)1/2 (A2
- x2)1/2 = (k/m)1/2 (A2 -
[Asin(wt)]2)1/2
= (k/m)1/2 A (1 - sin2(wt))1/2
= wAcos(wt)
A) Tpend = 2p(L/g)1/2 so Tleg = 0.8*2p(L/g)1/2 = 1.6 L1/2
B) d ~ 2Lsin10o = 0.35L
C) v = d/t = d/(0.5T) = 2d/T = 2*0.35L/1.6L1/2 = 0.44 L1/2
D) vSarah = 0.44 (1)1/2 = 0.44 m/s ~ 1 mph (reasonable)
E) vJesse = 0.44(0.7)1/2 = 0.37 m/s
A) For the mass & spring, PE ~ x2. For gravity, PE ~ y, so we want y ~ x2. Wire should be parabolic.
B) F(x) is of form Ax2 + Bx + C. The condition that F(0) = 0 sets B = C = 0. The condition that F(1) = a sets A= a. So F(x) = ax2.
C) PE = mgh = mgy = mgF(x) = mgax2.
D) Compare this situation to one we
understand
well, the mass on a spring.
Spring case: PE = ½ kx2,
KE = ½ mv2, T = 2p(m/k)1/2
Bead on wire case: PE = mgax2,
KE ~ ½ mvx2 (we're assuming vy ~
0)
T = ?
Comparison tells us that k <-> 2mga,
so by substitution, T = 2p
(m/2mga)1/2
= p(2/ga)1/2
MC1) (E)
A) Gauss' Law holds true for all closed surfaces, containing
any charge configuration.
B) The charge could be distributed into positive and negative regions,
with the total being zero.
C) Consider a point charge. The field is non-zero everywhere,
even where there is no charge.
D) Electric field lines diverge from positive charges.
E) Correct answer.
MC2) (D)
The net torque is clearly non-zero, like for the example we did in
class. However, the net force is also non-zero, because
the
field is stronger on the left side of the figure, where the field lines
are closer together.
MC3) (B)
All charges are integer multiples of e = 1.6x10-19 C.
Choice B corresponds to 1.5e.
MC4) (A)
For every bit of charge q in the ring, which produces a field at the
centre of magnitude Kq/R2, there is another bit of charge 180o
away which produces the same field at the centre but in the opposite
direction.
Since we can add these fields in pairs, the net field at the centre
will
be zero.
MC5) (C)
Each bit of charge qi in the ring will produce a potential
kqi/R at the centre of the ring. Since potential is a
scalar quantity, we need only add all of the potentials generated,
which
are all at distance R from the centre, to obtain a total potental of
kQ/R.
V = SVi = S
kqi/R
= k/R Sqi = [k/R]Q = kQ/R.
Gauss' Law: for a closed surface, fE
=
S Eperp DA
=
4pkqenclosed
Look at what the E-field looks like, using symmetry. Since the
spheres look the same as viewed from any angle, there is a spherical
symmetry
which implies that the E-field must be radial, and that the magnitude
of
E is the same for any given distance from the centre.
Choose the guassian surface to be a sphere of variable radius r
concentric
with the charged spheres. In that case, E is perpendicular to the
gaussian surface everywhere, so Eperp = E and
S Eperp DA
=
S E DA
and E is constant on the surface everywhere, so
S E DA = E SDA
= EA = E 4pr2 = 4pkqenclosed
Solve for E:
E = (kqenclosed)/r2
Now, look in each region to find E:
For 0 < r < rA, qenclosed = 0 and E
= 0
For rA < r < rB, qenclosed
= +Q and E = kQ/r2 radially outward (since q is +)
For rB < r < rC, qenclosed
= +Q + (-2Q) = -Q and E = k|Q - 2Q|/r2 = kQ/r2
radially inward (since q is -)
For rC < r, qenclosed = +Q + (-2Q) +
3Q = +2Q and E = 2kQ/r2 radially outward (since q is
+)
A)
Fe = kq1q2/r2 = 9x109*(1.6x10-19)2/(5.3x10-10)2
= 8.2x10-10 N
B)
Fe = FC = mw2r
w = [FC/mr]1/2 =
[8,2x10-10/9.11x10-31*5.3x10-10]1/2
= 1.3x1015 sec-1
C)
v = wr = 1.3x1015*5.3x10-10
= 6.9x105 m/s
Use the results from class that an infinite, flat sheet of charge
density
s
produces a uniform field of magnitude E = 2pkes.
The contribution to the total field at P from the positive sheet is 2pkes
up
and to the left. The
contribution
to the total field at P from the negative sheet is 2pkes
down
and to the left. Add these contributions as vectors
(taking
the diagonal of the square as the magnitude) to obtain:
Etotal = [(2pkes)2
+ (2pkes)2]1/2
= 2.82pkes
to
the left, regardless of
the
exact location of point P.
Start by assuming that the metal is a conductor, i.e., that
the
electrons are very free to move within the body of the metal. The
external E-field Eext will apply a force to each type of
charge,
but since the positives are lock inside the atoms, which in turn are
locked
in a lattice, we can ignore the force on the positives. The
electrons,
however, will begin to move in a direction opposite to the external
field.
An internal field, Eint, will be set up by virtue of the
separation
of the charges, so that the total field in the metal will be of
magnitude
||Eext| - |Eint||. Charges will continue to
move until the net field inside the metal becomes zero, at which time
there
will be no more forces to move the charge. The final state of the
metal will have negative charges one one side and positive charges on
the
other side, with zero net field on the inside.
MC2) (E)
Since the volume of the metal must remain constant, tripling the length
correspondingly cuts the cross-sectional area by three.
Given that Ro = rlo/Ao, then
Rnew = rlnew/Anew
= r3lo/(Ao/3) = 9rlo/Ao
= 9Ro.
MC3) (C)
Let the original capacitor have area A, plate spacing d, and therefor
capacitance Co = eoA/d.
Insertion of the third plate makes two series capacitors each of value
C' = eoA/(d/2) = 2Co.
Series capacitors combine by adding the inverses: 1/Ceq
= 1/2Co + 1/2Co = 2/2Co = 1/Co,
so the equivalent capacitance is once again Co.
MC4) (B)
This corresponds to going around the small left-hand loop
counter-clock-wise.
MC5) (D)
The 30W and the 60W
resistors are in parallel, and so experience the same potential
diference,
V. Assume that Ohm's relationship is correct, then
R30I30 = V = R60I60
30I30 = 60I60
I30 = 2I60
So, 2/3 of the current goes through the 30W
resistor.
A)
E = (-) DV/Dx
=
5000/0.01 = 500,000 V/m
B)
F = qE = 1.6x10-19*500,000 = 8x10-14 N
C)
DPE = qDV = 1.6x10-19*(-5000)
=
-8x10-16 J
D)
KEo + PEo = KEf + PEf
KEo = 0 (starts from rest)
KEf = 1/2mvf2
= - DPE = +8x10-16 J
vf = [-2*DPE/m]1/2
= 9.8x105 m/s (less than 0.1c, so calculation
is
O.K.)
Let each resistor Ri have a potential difference Vi and a current Ii. The three resitors are equivalent to a single resistor Req with potential difference Veq and current Ieq. Assume that 'Ohm's Relationship' holds true.
A)
We know that I1 = I2 = I3 = Ieq
because
charge is conserved.
We know that Veq = V1 + V2 + V3
because the electric field is a conservative field.
So,
Veq = V1 + V2 + V3
IeqReq = I1R1 + I2R2
+ I3R3
IeqReq = IeqR1 + IeqR2
+ IeqR3
Req = R1 + R2 + R3
B)
We know that I1 + I2 + I3 = Ieq
because
charge is conserved.
We know that Veq = V1 = V2 = V3
because the electric field is a conservative field.
So,
I1 + I2 + I3 = Ieq
Veq/Req =V1/R1 + V2/R2
+ V3/R3
Veq/Req =Veq/R1 + Veq/R2
+ Veq/R3
1/Req = 1/R1 + 1/R2 + 1/R3
Although each individual device may not draw more than 20 A, putting
them is parallel and turning them on may very well draw a total current
over 20A. This is dangerous, because the wires in the wall of the
house through which the current runs will get hot, possibly hot enough
to set fire to materials within the wall. Being metal, the fuse
element
will warm up also as more current passes through it. It is
carefully
designed to melt and break the connection (thus shutting down all the
devices
on that line) when a particular current is exceeded. The
procedure
after a fuse blows is to check the devices on the line, remove the
offenders
so that 20A will not be exceeded, and replace the fuse.
Occasionally,
when the home-owner was out of spare fuses, a copper penny was inserted
into the fuse socket to re-establish the connection, but the penny does
not melt, even at very high currents. This led to a good number
of
house fires, and also to the expression, 'putting a penny in the
fusebox,'
in reference to a dangerous, short term solution to a problem.
MC3) (D) Fm = qvBsinqv,B (RHR). Z is undeflected, even though sinq = 1, so Z must be uncharged. If X were positive, the RHR would indicate that the magnetic force would be down-and-to-the-right-ish; the force must however act toward the centre of the circular path, which is the other way, up-and-to-the-left-ish. We conclude therefor that X is really negative. Similarly for Y, which must also be negative.
MC4) (E) Use RHR to find m: curl fingers around with the current (CCW), and your thumb points out of the page. Now use the relationship that t = mBsinqm,B (RHR) and use the RHR to see that the torque points toward the top of the page.
MC5) (A) A bug would see two parallel, essentially straight
wires
(they curve over a distance much greater than their separation).
Let's use the field due to an infinite wire as an approximation.
So, the field that the lower loop 'feels' is moI/2pd.
The force acting on a short piece of length Dl
of the lower wire is then DF = BIDl
= [moI2/2pd]Dl
downward.
Add up all the forces on all the little bits to get:
Ftot = SDF = S[moI2/2pd]Dl
= [moI2/2pd]
SDl
= [moI2/2pd]
2pR = moI2R/d
A)
In the velocity selector, an electric force of magnitude qE acts
transversely
to the velocity of the charged particle, while a magnetic force of
magnitude
qvB acts in the opposite direction. These forces will cancel,
allowing
the particle to continue through undeflected, if
qE = qvB
E = vB
v = E/B = 5000/0.1 = 50,000 m/s
B)
In the spectrometer proper, the particle will be deflected into a
circular
path because the magnetic force, qvB, acts as a centripetal force, mv2/r.
qvB = mv2/r
q/m = v/Br = 5x104/[0.1*.016] = 3.1x107 C/kg
Convert this to e/amu:
(3.1x107 C/kg)(1.667x10-27 kg/amu)(1e/1.6x10-19
C) = 0.33 e/amu
The closest choice of those listed is tritium.
From the Biot-Savart Law, we have a notion that the B-field forms
circular
loops around the centres of the conductors.
Use Ampere's law to find the magnitude of B as a function of distance
from the central axis:
Sloop B|| Dl
= moIenclosed
Choose an Amperian Loop along one of the B-field lines, so that B is
always parallel to the loop (i.e., B|| = B) :
Sloop B Dl
= moIenclosed
Because of the rotational symmetry of the situation, we can assume
that the magnitude of B is constant all around the loop:
B SloopDl
= moIenclosed
We see that SloopDl
= 2pr, the circumference of the loop:
B2pr = moIenclosed
B = moIenclosed/2pr
How much current is enclosed by the Amperian Loop?
A)
For 0 < r < R, only I1 is enclosed by the Amperian
Loop, so
B = moI1/2prCCW
as seen in the figure.
B)
For r > R2, the enclosed current is I1 - I2:
B = mo(I1
- I2)/2pr CCW
You are not able to use Biot-Savart for the whole problem without
resorting to calculus.
Realize that placing the magnet near the iron bar makes the bar
temporarily
a magnet.
Place the objects as shown, where the magnet is black and the bar is
red:
In the left hand side, the induced south poles in the bar will have
a very strong attraction for the north pole of the magnet, and the N-N
repulsion will be weaker. In the right hand case, there will be
very
weak attractions between unlike poles, and even weaker repulsions from
like-pole pairs.
A)
Ferro-magnetic: neighbouring atoms' magnetic moments tend to line up
in the same direction.
B)
It may be so slightly. It appears that the total magnetic moment
is directed toward the top of the page and to the right. It's
certainly
not zero.
C)
One method to destroy the magnetic ordering is to heat the material
above the Curie Temperature. Then, the thermal energy available
is
more than sufficient to randomize the order imposed by the magnetic
interactions.
D)
A domain is a region is which the vast majority of magnetic moments
are oriented in the same direction.
E)
MC1) (C) If the transformer is indeed loss-less, then the
power
in equals the power out.
MC2) (E) Since the wire is placed symmetrically over the
loop, there are equal numbers of flux lines going into the loop through
the lower half as there are coming out of the loop through the upper
half.
Therefor, no matter what the current does, the total flux through the
loop
is constant at zero, and no emf is induced.
MC3) (E) There must be a capacitor, otherwise E
could not lag I. There must be a resistor, or else the phase
angle
would be either +90o or -90o. So, there
must
be at least R and C. We do not know if there is an inductor; if
there
were, 400 Hz must be lower than the resonant frequency.
MC4) (D) Consider the relationship at resonance for an
LC circuit, that wo = (LC)-1/2.
Then,
LC = w-2 = (seconds-1)-2
=
seconds2.
MC5) (C) At very low frequencies, the inductor
looks
like a wire (and therefor shorts the 100W
resistor)
and the capacitor looks like a break in the circuit (and so no current
runs through it):
So Irms = Erms/R
=
60/200 = 0.3 A
E = (-)DF/Dt = B DA/Dt = B*[N*pR2]/Dt = B[N/Dt]pR2 =3x10-5*5*p*92 = 0.038 volts
A)
IR = (-)L DI/Dt
B)
From relationship sheet: EL
= (-) I/R e-Rt/L = Eo
e0 = Eo = 6V
C)
I(t) = Eo/R e-Rt/L
= 6/20 e0 = 0.3 A
D)
I(t) = Eo/R e-Rt/L
=
6/20 e-20t/0.03 = 0.3e-667t
E)
0.15 = 0.3e-667t
0.5 = e-667t
ln(0.5) = -667t
667t = -ln(0.5) = ln(0.5-1) = ln(2)
t = ln2/667 = 0.001 seconds
Since R>>r, we can assume that the field in the toroid follows
closely
that of an infinite solenoid:
B = monI = moNI/2pR.
E = (-)N DF/Dt
= (-)N D[BA]/Dt
= (-)NA DB/Dt
= (-)NA D[moNI/2pR]/Dt
=
(-)[NAmoN/2pR[
DI/Dt
= (-)moN2pr2/2pR
DI/Dt
= (-)moN2r2/2R
DI/Dt
Now, we know that E = (-)L
DI/Dt,
so comparison to the result above yeilds that
L = moN2r2/2R
A)
wo = [LC]-1/2 = 7071
sec-1
B)
f = 2000 Hz => w = 2p*2000
= 12,566 sec-1
Z = [R2 +(wL - 1/wC)2]1/2
= 86 W
C)
Imax = Emax/Z
=
40/86 = 0.465 A
D)
(VR)max = ImaxR = 0.0465*4 = 1.86
V
E)
tanF = [wL -
1/wC]/R = [12,566*0.01-1/(12,566*2x10-6)]/4
=
21.5
F = arctan(21.5) = 87.3o
MC1) (E) - sinqC = nW/nG
nG = nW/sinqC
= 1.33/sin45o = 1.88
MC2) (D) - qi = qr.
We increase (or decrease) the reflected ray angle by the same amount as
the incident beam. The angle between this rays is the sum of qi
and qr, so that value changes by
2x17o = 34o.
MC3) (C) - m = -i/o = -8, so i = 8o 1/f
=
1/i + 1/o = 1/8o + 1/o = 9/8o
Then, o = 9f/8 = 9(.25)/8 = 0.28.
MC4) (D) - For the first polarizer, with unpolarized light,
I1 = 1/2Io.
For the second polarizer, I2 = I1cos2q
= [1/2Io]cos220o
For the third polarizer, I3 = I2cos2q
= [1/2Iocos220o]cos220o
= 0.39 Io
MC5) (C) - If the two sources were in phase, the
relationship
would be choice (A), but since they are one half cycle out of phase
already,
we remove the l/2 term to get choice (C)
Use Snell's Law for Refraction at each
interface, but do not calculate the individual angles.
n1sinq1
= n2sinq2
Since the surfaces are all parallel, the
angle of refraction at the first interface equals the angle of
incidence
for the second interface, and so on.
n2sinq2
= n3sinq3
n3sinq3
= n4sinq4
n4sinq4
= n5sinq5
n5sinq5
= n1sinq6
Back substitution shows then that
n1sinq1
= n1sinq6
sinq1
= sinq6
And since all angles are under 90o:
q6 = q1
= 11.2o
A)
511 (not 512, since we measure from the first line, counting it as
zero) in 0.33 m gives a separation of x = 0.33/511 = 6.45x10-4
m
B)
We know this from class to be from violet (4x10-7 m)
to red (7x10-7 m).
C)
Use Rayleigh's criterion: x/y = tanq = q
= 1.22l/D, where x is the separation between
lines and y is the distance the viewer is from the screen.
Calculate the minimum distance not to see distinct lines for
each colour:
yred = xD/1.22lred
= 6.45x10-4*0.003/1.22*7x10-7
= 2.27 m
yviolet = xD/1.22lviolet
= 6.45x10-4*0.003/1.22*4x10-7
= 3.97 m
So, a viewer must be at least 3.97 m = 13 ft away from the
screen
in order not to see the individual horizontal lines.
A)
Since the centre of the radius of curvature is on the shiny side of
the mirror, it is a concave mirror.
B)
The focal length f = r/2, so the focal point should be 6
cm in front of the mirror.
C)
D)
The image forms a distance 18 cm in front of the mirror.
E)
Since the image is upside down compared to the object, it is inverted.
F)
ho = 9.5 mm and hi = 19 mm (at least on my
printout).
|m| = hi/ho = 19/9.5 = 2
G)
The image is real, since these three rays actually cross.
| Type (Plane, Convex, Concave) |
|
|
concave | concave |
| Focal Length |
|
|
|
|
| Radius of Curvature |
|
|
|
|
| Object Distance |
|
|
|
|
| Image Distance |
|
|
|
|
| Image (Real/Virtual) |
|
|
|
|
| Image (Upright/Inverted) |
|
|
|
|
| Magnification |
|
|
|
|
First Column:
Plane mirror, so f = infinity
1/i + 1/o = 1/f = 0, so i = -o = -30
OR m = -i/o = +1, so i = -mo = -(1)(30) = -
30
Since m is positive, the image is upright.
Since i is negative (inside the mirror), the image is virtual
Second Column:
1/i + 1/o = 1/f ; 1/16
+ 1/(-12) = 1/f ; f =
-48
r = 2f = -96
Negative r means that the mirror is convex
m = -i/q = -(-12)/16 = + 0.75
m is positive, so the image is upright
i is negative, so the image is virtual (inside the mirror)
Third Column:
m = -i/o = -2; o = i/2 = 42.5
1/i + 1/o = 1/f ; 1/85
+ 1/42.5 = 1/f ; f =
28.3
r = 2f = 56.7
r is positive, so mirror is concave
i is positive, so image is real
m is negative, so image is inverted
Column Four:
r is positive, so mirror is concave
f = r/2 = 13.5
1/i + 1/o = 1/f ; + 1/o = 1/f - 1/i
= 1/13.5 - 1/(-71) ; o = 11.3
Since i is negative, the image is virtual
m = -i/o = -(-71)/11.3 = +6.25
Since m is positive, the image is upright.
MC2) translation + rotation + vibration => CV = U/nT = NA(3/2 + 2/2 + 2/2)kB = 7/2R (D)
MC3) The First Law is conservation of energy, and that is not violated here if the total energy only changes form. The Second Law specifically forbids this conversion without the production of waste heat, so it is violated. (B)
MC4) Since entropy is a state variable, its value at the beginning and the end of a closed cycle must be equal, so DS = 0. (E)
MC5) Isothermal => T is constant, so
from
the Ideal Gas Law, V ~ P-1, So if P -> 3P,
then
V -> V/3. (D)
A) We expect the total entropy to increase, since we have a closed system moving toward thermal equilibrium.
B) DS = Q/T = mLf /TICE = 200*80,000/273 = 58,610 calories
C) Since the same thermal energy was removed from the water as was provided to the ice, DS = Q/TWATER ≈ - 58,610 calories, actually a bit less because TWATER > TICE. The exact answer depends on how much warmer the water is than the ice.
D) DStotal = sum of answers to Parts B and C, i.e., close to zero , but positive.
E) The important consideration is that the lake had to cool ever so
slightly in order
to provide the energy to warm the ice, so the average temperature of
the
lake during this process was actually above 0o. Using
that correct value makes the answer to Part C less negative than we
thought,
and so the net change in S is really positive, as we initially
expected.
A) The work is the area enclosed by the PV curve, W = (3Po - Po)(2Vo - Vo) = 2PoVo.
B) We'll need the temperatures at each state; find them with the
Ideal
Gas Law: P = (nR/V) T for isochoric processes, and V = (nR/P) T for
isobaric
processes.
Then, if T = To at the lower left corner,
T = 3To at the upper left (P tripled, V same)
T = 2To at the lower right (V doubled, P same)
T = 6To at the upper right (V doubled, P tripled)
Also make use of the facts that CV = 5/2R
and
CP = 7/2R for this type gas.
Then, in CW order from the lower left of the cycle diagram:
Q = nCVDT = n5/2R(2To)
=
5nRTo = 5PoVo (in)
Q = nCPDT = n7/2R(3To)
=
21/2nRTo = 21/2
PoVo (in)
Q = nCVDT = n5/2R(-4To)
=
-10nRTo = -10PoVo (out)
Q = nCPDT = n7/2R(-To)
=
- 7/2nRTo = -7/2PoVo
(out)
C) eff = W/Qin = 2PoVo/[5PoVo
+21/2
PoVo] = 4/31 = 13%
A)
B) Few molecules are seen at high temperatures, since they tend to lose energy to slower ones through collisons. There are also few molecules at low speeds, since they tend to pick up energy from collisions with faster ones.
C)
D) The peak is lower, since the same number of molecules are spread
over a greater range of speeds. The curve shifts to higher
velocities,
since T is a measure of the rms speed.
Start with the First Law:
Q = W + DU
Consider the addition of thermal energy through an isochoric process:
Q = nCVDT and W = 0, so that the
First law becomes
nCVDT = 0 + DU.
Now, consider an isobaric process: Q = nCPDT
and
W = PDV, so that the First Law becomes
nCPDT = PDV
+
DU.
From the Ideal Gas Law, PDV = nRDT
for an isobaric process, and we've already shown that nCVDT
= DU.
Substitution of these terms results in
nCPDT = nRDT
+
nCVDT
CP = R + CV