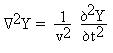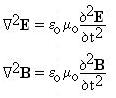Section 2-7 - AC Circuits

AC Resistor Circuit
RMS Values
AC Capacitor Circuit
AC Inductor Circuit
LC Circuit
Driven LRC Series Circuit
Maxwell's Equations
Correlation to your Textbook

AC Resistor Circuit

We've already discussed briefly in the last section the situation where the emf in a circuit is not constant, as for a battery, but rather varying in time.  Often, the variation is periodic and involves a reversal of the direction of the emf.  These emfs cause currents which alternate direction, and are therefor referred to as AC currents (yes, it is redundant; 'AC' stands for alternating current).  The symbol for such an emf is a circle with the waveform of the emf inscribed; for example a sinusoidal emf is represented by

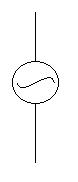
and a square wave emf should appear as follows.

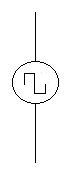
We will concentrate on the sinusoidal emf for two reasons: first, it is fairly easy to work with mathematically, and second, just about any other shape curve can be approximated with a combination of sine waves, so any general results we obtain should be true for other waveforms as well.

Let's consider a sinusoidal emf of the form e(t) = emax sin(wt + f) that is connected to a resistor:

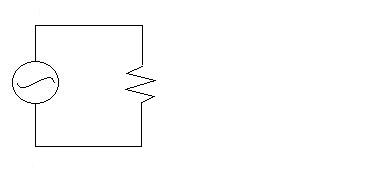
Here, the phase angle f allows us to change the sine to a cosine or any combination of the two.
N.B.: We need to be very careful about the signs in the next few sections.
e(t) = emax sin(wt + f)
The voltage drop across the resistor is (by Kirchhoff's Loop Rule) equal to the voltage rise across the emf source:

VR(t) = e(t)

so, VR = emax sin(wt + f) = VRmax sin(wt + f)
and by Ohm's relationship,
I = [VRmax/R] sin(wt + f) = Imax sin(wt + f).
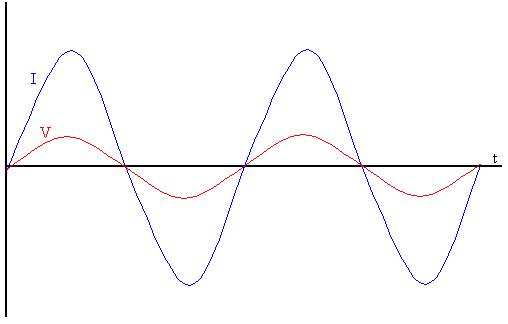
So, we find, very unsurprisedly, that the current through and the voltage drop across a resistor are in phase with one another, that is, they peak at the same time, are zero at the same time, et c.

RMS Values

Now, before we move on to the capacitor circuit, let's introduce some new terms.  Consider the power dissipated in this resistor as thermal energy; instantaneously, we have that
Pinstant = I2R = R[Imax sin(wt)]2 = R Imax 2 sin2(wt).   Note that here, I've dropped the phase angle term for simplicity; it can always be replaced later.
Now, suppose that we want to find the average power dissipated.  The average of the square of the sine (over one cycle) is 1/2.  We can see this easily by looking at the graph,

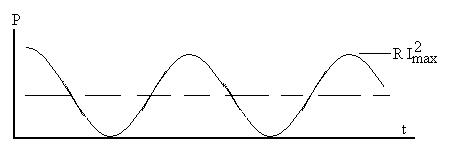
realizing that the area under the curve represents energy, mentally cutting off the 'mountains' above 1/2R(Imax)2 and seeing that they fit exactly into the 'valleys,' forming a nice straight horizontal curve given by
Paverage = 1/2R Imax2.
Or, we can do this more mathematically:  In general, the average of a function over interval (a, b) is given by
FAVE = [ ab F(z) dz ]/[ab dz],
so we get in this case (T = 2p/w is the period of the cycle),
PAVE = [ 0T R Imax 2 sin2(wt + f) dt ]/[0T dt] = [ R Imax 2  1/w [1/2wt - 1/4 sin(2wt)] 0|T ]/[T]
                =  R Imax 2  1/wT [1/2wT - 1/4 sin(2wT)] = R Imax 2  1/wT [1/2wT - 1/4 sin(2w(2p/w))] = R Imax 2  1/wT [1/2wT - 1/4 sin(4p)] = 1/2 R Imax 2 .
Suppose that we ask what effective DC current would be necessary to provide the same average power as this oscillating current does, i.e.,
Paverage = RIeffective2 ?
By comparing, we see that Ieffective = Imax/(2)1/2.
This particular result, called the r.m.s.,or root-mean-square, current, is valid only for the sinusoidal function.  Other shaped curves will have different rms factors, which are calculated in the same way: we took the current, squared it, averaged it, and then took the square root again.
We could have done the same thing with the voltage, finding that Vrms = Vmax/(2)1/2, so that
Paverage = Vrms2/R = Vrms Irms.

The voltages and currents listed on household AC appliances are actually rms values:  the given voltage standard of 110 VAC means that the maximum voltage is about 155 V.  A circuit breaker rated at 20 A will allow a peak current of 28.2 A.
Let's find the rms value of a square wave current:

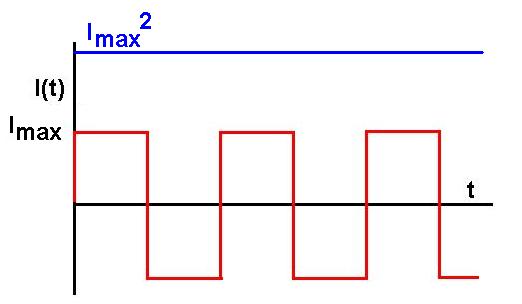
So this one is easy.  Both the positive and negative portions square to give Imax2.  The average of this is clearly Imax2, and the square root of that is clearly Imax.
Try a harder one, the sawtooth wave:

The equation for the current is
I(t) = Imax [2t/T - 1] over the first cycle (other cycles have similar expressions).
Square it:
I2(t) =  Imax2 [4t2/T2 - 4t/T + 1]
Now, average over one cycle:
[ 0T Imax2 [4t2/T2 - 4t/T + 1] dt ]/[0T dt] = Imax2 [ 0T  [4t2/T2 - 4t/T + 1] dt ]/[T] = Imax2 [[4t3/3T2 - 4t2/2T + t] 0|T ]/[T] =
                         Imax2 [4T3/3T2 - 4T2/2T + T]/[T] = Imax2 [4/3 - 4/2 + 1] = Imax2/3
Then, take the square root to find the rms value:
Irms = Imax/(3)1/2.

AC Capacitor Circuit

Consider a capacitor in series with a sinusoidal AC emf of the form
e(t) = emax sin (wt).

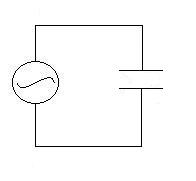
The voltage drop across the capacitor will be, by Kirchhoff's Loop Law,
VC(t) = emax sin (wt) = VCmax sin (wt).
But we also know that the voltage drop across the capacitor is q/C, so let's find q(t):
q(t) = C VC = CVCmax sin (wt).
We'd like to to find the current, I(t), which we recognize as the rate at which charge accumulates on the capacitor, I = dq/dt.  So,

I(t) = w CVCmax  cos (wt).

This result tells us two very interesting things:

1) The current into the capacitor is not in phase with the voltage difference across it; in fact, we can say that the current leads the voltage drop across the capacitor by 90o, or by one fourth of a cycle:

2) We can write an expression resembling Ohm's Relationship between the maximum current and the maximum voltage drop.  We see from the result that the maximum current is given by
Imax = w CVCmax ,
or
VCmax = [1/wC] Imax.
The quantity [1/wC] is somewhat similar to the resistance in that it is a measurement of the degree to which the capacitor inhibits charge flow in the circuit; its units will be ohms, just like for resistance.  Most interestingly, it will be frequency dependent; at low frequencies, very little current will be able to flow, while at high frequencies, the current will be large.  Since this quantity looks useful, let's give it its own name and symbol: the capacitive reactance, cC = 1/wC. Once again, just to be very clear, the maximum voltage drop across the capacitor and the maximum current do not occur at the same time.

AC Inductor Circuit

Consider an inductor in series with a sinusoidal AC emf of the form
e(t) = emax sin (wt).

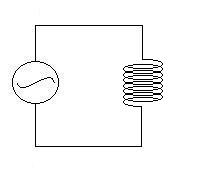
The voltage drop across the inductor will be, by Kirchhoff's Loop Law,
VL(t) = emax sin (wt) = VLmax sin (wt).
We also know that the voltage drop is actually an emf developed across the inductor,  e(t) = - L dI/dt, so the voltage drop will be +L dI/dt.  So,
VLmax sin (wt) = + L dI/dt,
or,
dI/dt = [VLmax/L] sin (wt).
We'd like to to find the current, I(t).  Let's try integrating:
dI = [VLmax/L] sin (wt) dt
I = [VLmax/L] sin (wt) dt = - [VLmax/wL]cos (wt) + Constant  (the constant can be set to zero, since we have no expectation of a DC component).
I(t) = - [VLmax/wL]cos (wt).

This result tells us two very interesting things:

1) The current through the inductor is not in phase with the voltage drop across it; in fact, we can say that the current lags the voltage drop by 90o, or by one fourth of a cycle.

2) We can write an expression resembling Ohm's Relationship between the maximum current and the maximum voltage drop.  We see from the result that the maximum current is given by
Imax = [1/wL] VLmax ,
or
VLmax = [wL] Imax.
The quantity [wL] is somewhat similar to the resistance in that it is a measurement of the degree to which the inductor inhibits charge flow in the circuit; its units will be ohms, just like for resistance.  Most interestingly, it will be frequency dependent; at high frequencies, very little current will be able to flow, while at low frequencies, the current will be large.  Since this quantity looks useful, let's give it its own name and symbol: the inductive reactance, cL = wL.  Once again, just to be very clear, the maximum voltage drop across the inductor and the maximum current do not occur at the same time.

LC Circuit

Consider a circuit comprising a capacitor and an inductor, only.

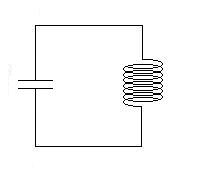
Let's charge up the capacitor, then connect it to the inductor.  

Let's write a Kirchhoff's Loop Law equation to describe this.  Here we have the voltage drop across the capacitor on the left, and the emf of the inductor on the right.  For reasons which may eventually become apparent, we'll define positive q to be when positive charge resides on the lower plate of the capacitor, and positive current to be clockwise around the circuit.  Then,
VC  = eL
[1/C]q = - L dI/dt
+L dI/dt + [1/C]q = 0
+L d2q/dt2 + [1/C]q = 0.
This is an equation we've seen before, and which we spent much time and effort solving.  Then, it was written
ma + kx = 0,
which is Newton's Second law written for a mass on a spring.  Remember that 
v = dx/dt and 
a = dv/dt = d2x/dt2, so
m d2x/dt2 + kx = 0.
This equation is easily solved, but we will instead make use of the analogy with the mass-spring system to figure out the behaviour of the LC circuit.  For a mass on a spring, the solution is:

x(t) = A cos(wot + f) with a natural frequency of oscillation wo = [k/m]1/2.

Which quantities in each system are analogous?
displacement x charge on capacitor q
velocity v = dx/dt current in circuit I = dq/dt
acceleration a = dv/dt                 dI/dt

It appears that these are also analogous:
mass m inductance L
spring constant k capacitance 1/C
Does that make any sense?  The mass is a measure of the system's inertia, that is, the how much the system would like to stay at rest (v=0) if it's already at rest, and stay in motion if it's already in motion.  The inductance 'wants' to keep the current zero if it's already zero, and maintain its value if it's not zero.  The capacitor, on the other hand, always tries to return the system to an equilibrium state, much as the spring pushes the mass back toward the equilibrium point.

We can therefor guess that the solution to the LC circuit equation is:
q(t) = qmax cos(wot + f) with wo = [1/LC]1/2.
That is, every time this LC circuit is set in oscillation, it will do so at this natural frequency.

In the mass-spring system, we saw that the energy changed form from kinetic to potential, back to kinetic, et c.  We already know from our discussions of RC and LR circuits that capacitors and inductors store up energy.  If we take the expression for spring potential energy and substitute 1/C for k and q for x, we obtain
1/2kx2 1/2[1/C]q2
which we proved is the energy stored in the capacitor.  If we take the kinetic energy and replace m with L and v with I, we get
1/2mv2 1/2LI2
That is, the energy stored in an inductor is 1/2LI2, as was asserted without proof in the last section, and which we have now shown through analogy.  So, we see that the energy in an LC circuit is stored first in the electric field in the capacitor, then as magnetic energy in the inductor.

What else?  The total magnetic flux in the inductor is fM = LI, which is analogous to the momentum, p = mv.  Faraday's Law, VL=+LdI/dt then is analogous to the Newton's Second Law: F=mdv/dt.
The electric flux fE in the capacitor appears not to correspond directly with any quantity in the mechanical example, but Gauss's Law for Electricity (the surface surrounds one plate of the capacitor) does appear to imply Hooke's Law:
fE = q/eo
eo[EA] = q
eoEA[d/d] = q
[eoA/d][Ed] = q
C[-V] = q
V = -[1/C]q    => F = -kx

What if there had been a small resistor in the circuit?  This RI terms plays the same role as a drag force, removing energy from the system; after every half-oscillation, the capacitor charges up just a little bit less.  As the energy is removed, the oscillations (at a frequency close to, but not quite equal to [1/LC]1/2) will decay in amplitude.

Driven LRC Series Circuit

When we investigated the mass-spring system with drag, we discussed a way in which we could put energy back into the system.  What was it?

Here, we will introduce energy by applying a driving emf, which we shall assume is sinusoidal with frequency w, which may well be different than wo.  Remember that, after a short period of combined frequency motion, the system will eventually oscillate at the driving frequency.

We start with the notion that, in a series circuit, there is only one current, I, and that the voltage drops over the resistor, capacitor, and inductor must sum up to the voltage rise from the emf.  Now, we COULD try to solve this differential equation:

L d2q/dt2 + R dq/dt + 1/C q = emax sin (wt + f).
Instead, let's introduce a method by which we can easily keep track of what's going on in the steady state.
Suppose that we wish to represent a function of the form
A(t) = Amax cos(wt).
Instead, we consider a phasor (A), a quantity which, like a vector, has magnitude but, unlike a vector, has phase instead of direction.  The phasor A is represented by an arrow, the length of which is proportional to the maximum value A can have.  We plot the arrow on axes which reperesent real and imaginary values (remember that imaginary numbers are multiples of the square root of minus one, called 'i' by physicists and mathematicians, 'j' by engineers).

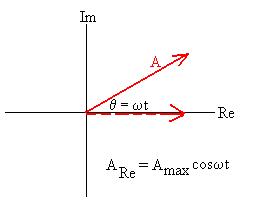
The quantity we are actually interested in is the projection of the phasor along the real axis, or if you prefer, the real component of the phasor.  This is given by
Re (A) = Amax cos q.
To account for the oscillation in A, we will rotate the arrow around the origin at frequency w, so that
q = wt
and
A(t) = Re (A) = Amax cos wt.
To illustrate:

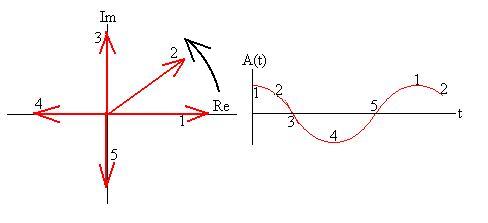
As the arrow turns counter-clockwise, the real component of the phasor matches the actual value of A; at Point 1, A is at its maximum, as is the real part of the phasor; as time progresses to Point 2, the value of A decreases as does the real component of the phasor, until each is zero at Point 3, and so on.

Let's use this method to construct a phasor diagram for what's happening in the driven LRC series circuit and, from it, derive some useful relationships.  We'll actually construct the diagram backwards, in the sense that we'll start with the current and end with the emf, even though in reality, the emf drives the current.  Pick a phase for the current I, keeping in mind that the arrow will rotate around the origin at frequency w:


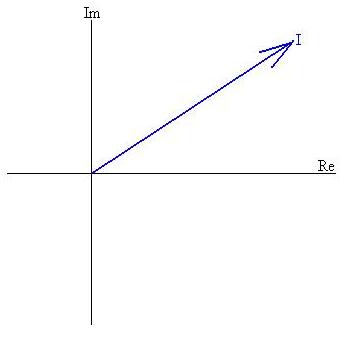
We already worked out the phase relationships between the current and each of the voltage drops.  For example, we said that the current through the inductor lags the voltage drop by 90o, so we should draw in the inductor's phasor 90o ahead, or counter-clockwise, of the current's phasor:

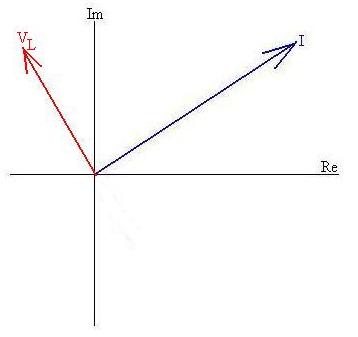
where, again, the length of the arrow tells us the maximum value of that voltage drop, with VLmax = wL Imax.  Let's put in phasors for VR (in phase with I) and VC (90o behind I):

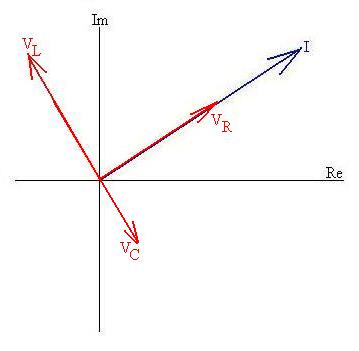
Keep in mind that this is a generic diagram; we have no idea how long to make the arrows.  Also remember that the whole system of arrows is rotating counter-clockwise with frequency w.
From Kirchhoff's Loop Law, we know that e = VL + VC + VR, and so we can say that this is true of the phasors representing them as well, since
e = emax cos(wt)    Here, f is the as yet unknown angle between the emf and the current.
VL = VL max cos(wt + p/2)
VR = VR max cos(wt)
VC = VC max cos(wt - p/2).
So, we can put in the phasor representing the emf as the 'phasor sum' of the voltage drops:

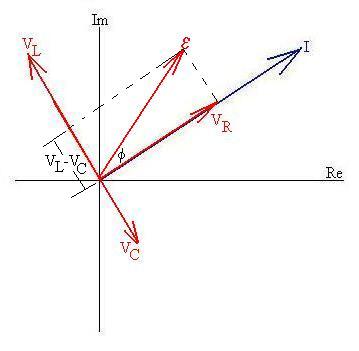
Since VL and VC are in opposite 'phases,' the component of the emf in that 'direction' is VLmax - VCmax, where we remember that VCmax could very well be larger than VLmax, in which case the emf would be on the other side of I, i.e., lagging behind I.

Now, we can work out some interesting relationships:

tanf = [VLmax - VCmax]/VRmax = [cLImax - cCImax]/RImax = [cL - cC]/R = [wL - 1/wC]/R.
tanf = [wL - 1/wC]/R.

emax = [VRmax2  + (VLmax - VCmax)2]1/2 =  [(RImax)2  + (cLImax - cCImax)2]1/2 = [(R)2  + (cL - cC)2]1/2 Imax
Here we once again have a relationship which looks a little like Ohm's Relationship.  Let's give the quantity in brackets its own name, the impedance Z:
Z = [(R)2  + (cL - cC)2]1/2
so that
emax = Z Imax
Keep in mind that the maximums in the emf and the current will generally not occur at the same time. 
We can see that the amplitude of the current in the circuit will be greatest when Z is smallest, and that will occur when
cL - cC = wL - 1/wC = 0,
or when w = [1/LC]1/2 = wo.
So, just as for the mass-spring system, the greatest response will occur when the driving frequency matches the natural frequency, a condition refered to as resonance.
In that situation, Z = R, and f = 0, and the circuit behaves as if it were purely resistive (i.e., emax = R Imax and e and I are in phase), since the capacitive and inductive effects cancel each other exactly.
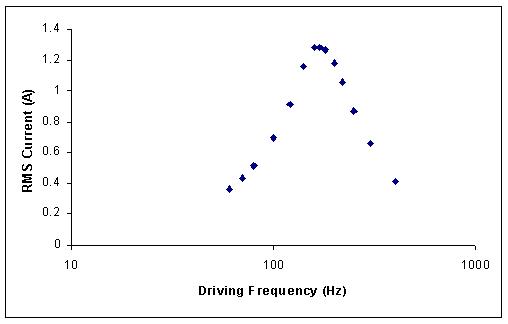
Here are the results of measurements on an RLC circuit with L = 8.3mH, C = 100mF, and R = 5.5W.  The maximum amplitude current occurs (as predicted) when the driving frequency is fo = 1/[2p(LC)1/2] = 175 Hz.

What power is dissipated in this circuit?  The energy leaves as thermal energy through the resistor, and the instantaneous energy lost there is
Pout = VR I.
The average power (assuming sinusoidal functions) is then
Pout average = 1/2 VRmax Imax = VRrms Irms.
From the diagram above, it should be clear that
emax = VRmax cosf,
so that
Pout average = 1/2 emax Imax cosf = erms Irms cosf.
These expressions of course also represent the power into the circuit in the steady-state situation.  The cosine term is often referred to as the power factor of the circuit.

Mastery Question

Find the impedance as a function of frequency for a driven LRC parallel circuit.  Click here for a solution.

Additional Neat Note
You can probably imagine that combinations of inductors, capacitors, and resistors can be used to build analog circuits that will output the derivatives or intergrals of mathematical functions, so long as those functions can be represented by a time-varying voltage.  Do a Google search in your free time.

Maxwell's Equations and EM Waves

Let's return briefly to Ampère's law:
 B|| dl = moIencl
Consider a wire carrying current I and a point P at which we want to find the magnetic field caused by that current.  We draw a loop around the wire and evaluate the integral on the left hand side of Ampère's Law, and find that the result is proportional to the current enclosed by the loop.  How exactly do we determine if a loop encloses a current or not?  One way is to consider a surface (yellow in the figure below) that is bounded by the loop; if the current penetrates from one side of the surface to the other, then the loop encloses the current.

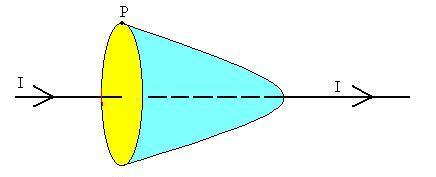
However, there can be many surfaces bounded by a given loop.  Consider for example the blue surface in the upper figure.  Since the current I also passes from one side of the blue surface to the other, we should get the same result for the field at P.

Now, place a capacitor in the wire as shown below.

Let's calculate B at P again.  Using the yellow surface, we arrive at the same answer as above, but using the blue surface, we get zero, since there is no current pentrating the surface.
Maxwell (see note) recognized this problem and postulated that the changing electric field between the plates of the capacitor might also be responsible for causing magnetic fields.  He modified Ampère's Law in the following way:
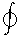 B|| dl = moIencl  + moeo dfE/dt.
Let's investigate further (assuming all of our approximations for a parallel plate capacitor hold true):
fE = EA = [s/eo]A = [Q/Aeo]A = Q/eo
Not surprising, considering Gauss's Law for Electricity and the fact that the E-field is zero except between the plates of the capacitor.  Then the extra term becomes:
moeo dfE/dt = moeo d[Q/eo]/dt = mo dQ/dt = mo I.
This flux term, eo dfE/dt, is then numerically equal to the real current in the wire and is referred to (for historical reasons) as the displacement current.

The set of four equations we have been working with are now collectively known as Maxwell's Equations:
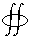Eperp dA = qencl/eo     Gauss's Law for Electricity
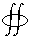Bperp dA = 0     Gauss's Law for Magnetism
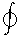 E|| dl =  (-) dfM/dt   Faraday's Law of Induction
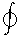B|| dl= moIencl + moeo dfE/dt     Maxwell's modified version of Ampere's Law

Maxwell's contribution tells us that, in much the same way that a changing magnetic field can cause an electric field, a changing electric field can create a magnetic field.  Before we discuss the incredible importance of this notion, we need a little background.

Mechanical waves obey a specific differential equation called the wave equation (we worked this out for transverse waves on a string in PHYS 1):

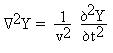
Y represents some quantity's deviation from an equilibrium value (such as the transverse displacement of a string) and v represents the speed of the wave.  For the case of  wave on a string, it can be shown fairly easily that this corresponds to a combination of Hooke's Law and Newton's Second Law (e.g., d2Y/dt2 is the transverse acceleration, 1/v2 is proportional to k/m, et c.).
If we take somewhat more mathematically sophisticated versions of the Maxwell equations and combine them, we obtain two wave equations:

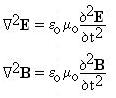
along with some other interesting results.  There is a very good algebra-based derivation of this result in Weidner and Sells, Elementary Classical Physics, Allyn and Bacon, Boston (1973).
The implication is that it may be possible to have electro-magnetic waves, which travel through vacuum with speed
v = 1/(moeo)1/2.
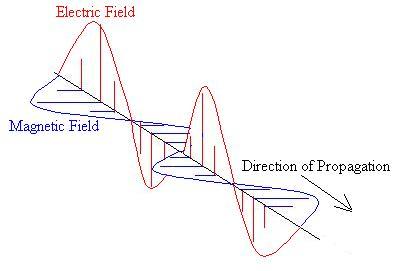
However, the E and B fields must be at right angles to each other and to the direction of propogation of the wave (in fact, v is parallel to E x B), and at any point,
B = E (moeo)1/2.
In addition, the wave carries energy with an average intensity of
Iave = E B/2mo

Calculate the speed of these EM Waves in vacuum, given that v = 1/(moeo)1/2.

We'll discuss the implications of this result in the next section.

Note
Maxwell did this interesting work, but presented his results in a very complicated mathematical framework.  We usually credit Heaviside with the present formulation of the equations.



D Baum 2001, 2003