Section 1-5 - Circular Motion - up to dat in Oct 3rd.
Centripetal Acceleration
Applications
&
Examples of Centripetal Acceleration
Correlation
to your Textbook
Centripetal Acceleration
The second half of Newton's First Law of Motion says that an object
will
maintain a constant velocity unless acted on by a force. So, whem
we see an object moving along a circular path, even at constant speed,
we know that there is a force acting on it: changing velocity
(direction)
means that there is an acceleration, which means (Second Law) that
there
is a force.
Let's consider a ball whirled around on the end of a string (ignore
any gravity for now). What force acts on the ball to keep it
moving
in a circle?
If that force were removed, what
would be the subsequent motion of the ball?
Because this force acts on the ball
toward the centre of the circle (see below), it is sometimes referred
to
as a centripetal force (centripetal = 'seeking the
centre').
However, in my experience, this causes a great deal of confusion in
many
students who count the centripetal force as a separate force; better to
say that 'a force acts centripetally.'
Let's look at this situation in
more
detail. Let an object move at constant speed around a circular
path.
Consider a particular point in the object's path, where the velocity
vector
v
is then tangent to the circle:
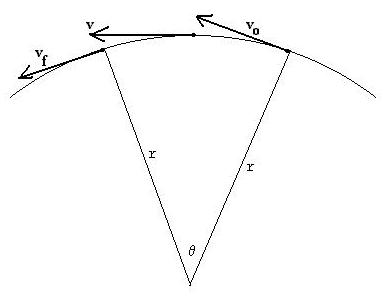
Let's also look just before this point (vo ) and
just after this point (vf ), so that it takes time Dt
to get from the first to the last point. These three vectors have
the same magnitude (speed is constant) even though the directions are
different.
Since the velocity changed, there was an acceleration. How big
and
in what direction is the change, Dv?
Let's move the velocity vectors around so that they are tail to tail:
Dv is the vector which needs to
be
added to vo to get the final result, vf.
As the figure shows, Dv points
toward
the centre of the circle. Since a = Dv/Dt,
the direction of the acceleration is the same as for Dv,
and so this is a centripetal acceleration. Strictly
speaking,
we just found the average acceleration, but if we were to make the time
interval Dt smaller and smaller, then the
average
value approaches the instantaneous value, as we've seen before.
Now for the magnitude of aC:
Instantaneous aC = lim Dt->0Dv/Dt.
First, we have to realize that the angle between the two velocity
vectors
is the same as the one labelled q in the
original
figure. We can argue that the velocity vectors, being tangent to
the circle, are always at right angles to their corresponding location
vectors (the r's), so that as r swings through a given
angle,
then v must swing through the same angle.
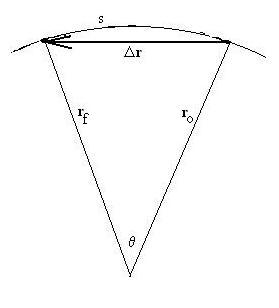If that's true, then we see that we have two similar triangles, one in
real space, the other in velocity space; each is isosceles (since |vo|
= |vf| = v and |rf| = |ro|
= r) and they have the same apex angle). In that case, we can
write
a relationship involving the lengths of the sides of these triangles:
Dr/r = Dv/v,
or Dv = v Dr/r.
Then,
aC = lim Dt->0 Dv/Dt
= lim Dt->0 [vDr/r]/Dt
= lim Dt->0 [v/r][Dr/Dt]
= [v/r] * lim Dt->0 [Dr/Dt]
But, as the time interval is made smaller, the displacement, |Dr|,
approaches in value the distance, s, traveled by the object along the
arc
of the circle:
lim Dt->0 [Dr/Dt]
= s/Dt,
and s/Dt is the speed, v, of the object,
so
aC = [v/r]*[s/Dt] =[v/r][v] =
v2/r.
So, in short, an object moving at constant speed about a circular
path
has an acceleration which points toward the centre of the circle
(centripetal)
for which the magnitude is v2/r.
What causes this acceleration? There must be some force or
forces
which have a net component in the direction of the centre of the
circle:
Si (Fi)C
= maC = mv2/r.
Forces which act away from the centre of the circle should be assigned
a negative sign in the sum.
Forces or components of forces perpendicular to the line connecting
the object to the centre of the circle are referred to as tangential
forces or components, for which we can write
Si (Fi)T
= maT.
The meaning of this will be clearer after a later discussion.
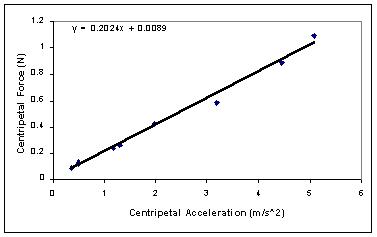
Here are the results of an experiment that will verify the
centripetal force
relationship
above. The speed of a pendulum bob was measured at the lowest
point
in its swing, while the tension in the string was measured
simultaneously
with a force transducer. In this graph, the net centripetal force
is plotted against the centripetal
acceleration;
the slope should be the mass (0.2 kg in this trial):
Let's return briefly to the derivation above. What if the
speed
of the object had not been constant? Two things:
We would have had to replace the step,
s/Dt is the speed, v, of the object,
with
lim Dt->0 [Dr/Dt]
= lim Dt->0 s/Dt=
vinstantaneous.
Also, there would had had to have been a component of the acceleration
along the direction tangent to the circular path, which we would then
have
called the tangential acceleration. But, there would
still
have been a centripetal component as described.
One last note: occasionally, problems are given using the angular
velocity,
w.
This is the number of radians per
second (Dq/Dt)
through which the object travels about the centre of the circle.
Since the arclength is given by
s = rq,
then the tangential speed is given by
v = Ds/Dt = D[rq]/Dt
= rDq/Dt = rw,
so that
aC = v2/r = w2r.
Applications
and
Examples of Centripetal Acceleration
Consider a bob of mass m being whirled at the end of a string in a
horizontal
circle of radius r at constant speed v. What is the tension in
the
string if gravity is ignored?
We consider the bob at some instant in its travels and make our
co-ordinate
system such that one axis points toward the centre of the circle.
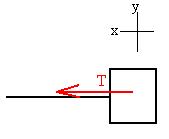
We consider any force pointing toward the centre to be positive and
any force pointing away to be negative, and we write Newton's second
law:
SiFi=
maC.
T = maC = m[v2/r].
Now, what difference would it make if gravity were present?
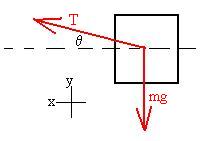
Assume that the string makes an
angle q
with the horizontal. Then,
C: SiFi=
maC => Tcosq
=
m[v2/r].
y: SiFi=
may => T sinq -
mg = 0 => T sinq = mg
Combining these by dividing the second by the first, we obtain:
tanq
= gr/v2,
which may be of interest in a given problem or not.
In such a case, can the string ever be exactly horizontal?
Consider a
coin on a moving turntable. What must be the minimum co-efficient
of static friction (for a given speed and radius from the spindle) in
order
that the coin not slide off?
Align the
axes so that the x-direction i stoward the centre of the circular path
of the coin, and the y-direction is vertically upward.
Write Newton's
second law:
SiFi=
ma.
N - mg = may = 0
Ff = max = maC = mv2/r.
Ff = mSN (in the
critical
case of the coin just about to slide).
Through substitution (not shown here) and cancellation of the mass
from each side in the result, we obtain:
(mS)MIN = v2/gr.
So, the mass of the coin doesn't matter (dime or half-dollar), and
consistent with our experience, the coin is more likely to slide at
greater
speeds and at smaller radiuses.
The same results are applicable to a car driving in circles on a flat
parking lot; the static friction between tires and road provide the
centripetal
force. If the car attempts to make a turn at too high a speed, or with
too tight a radius of curvature, it will begin to skid to away from the
circle's centre.
How do highway engineers minimize the necessity of friction for
turning
cars along bends in the road?
How does this help? Consider
the figure below.
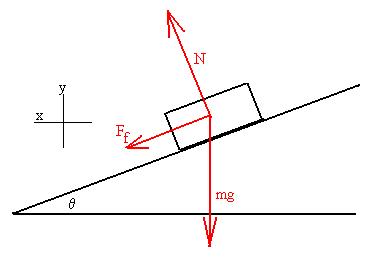
We shall draw in the friction down
the incline, parallel to the surfaces of the road and tires, keeping in
mind that we can reverse the direction later by inserting the negative
of the value of the co-efficient. We shall orient the axes so
that
the (centripetal) acceleration is directed along the x-axis; we assume
that we want the vertical acceleration to be zero.
x: Ff cosq
+ Nsinq
= maC = mv2/r
y: Ncosq
- Ff sinq - mg = may
=
0
Ff = mSN (in the
critical
case)
Again, we re-arrange and substitute. Since we haven't stated
a problem yet, let's eliminate N and Ff, keeping the stuff
we
might be interested in like m, q, v, and r.
Substitute the friction relationship into the second equation:
Ncosq
- [mSN]sinq -
mg = 0
N[cosq
- mSsinq] =
mg
N = mg /[cosq
- mSsinq]
Now, substitute this and the friction relationship into the first
equation:
[mSN]cosq
+ Nsinq
= mv2/r
N[mScosq
+ sinq]
= mv2/r
[mg /[cosq
- mSsinq]][mScosq
+ sinq]
= mv2/r
[mScosq
+ sinq] /[cosq
- mSsinq]
= v2/gr.
First, we see that the mass drops out, so any result is just as valid
for a VW Bug as for a big truck. This is a good thing, otherwise,
cars and trucks would each have their own roads (hey there's an idea!).
Let's see what else: in the winter, the roads can get very icy so that
the co-efficient of friction drops to about zero. At what angle
should
the road be banked so that cars can make it around the curve at the
speed
limit, even in winter? Set mS
= 0:
[sinq]
/[cosq]= v2/gr
tanq= v2/gr.
Now, suppose that we want to turn at 70 mph (=31 m/s) in a radius of
a quarter mile (0.4 km) without relying at all on friction. At
what
angle should we bank the road?
On that same curve, what maximum
speed could we have and not skid off the road, if mS
between rubber and concrete is 0.9?
Snide comments aside, what exactly
does a spoiler do?
Why does that help?
What is the minimum speed at which
this turn could be negotiated?
Why did that happen?
Mastery Question
Consider a hoop which rotates at speed w about
its vertical diameter. A bead of mass m can slide frictionlessly
along the wire.
a) Find all positions on the wire at which the bead is in equilibrium,
as a function of the angle between the bead and the lower-most point on
the hoop, as seen from the centre of the loop.
b) Show that there is a critical value of w such
that the behavior of the bead is different for
w<wCthan
for w>wC.
Click here for Solution.
Return to Notes Directory
Continue to Next Section of Notes
D Baum 2000