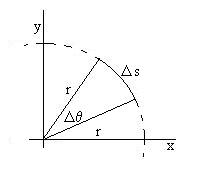Section 1-8 - Rotational Motion -
Rotational Kinematics
Torque
Newton's
Second
Law
for Rotation and the Moment of Rotational Inertia
Rotational Kinetic Energy
Angular Momentum
A Note on Rolling Objects
Mastery Question
Correlation
to
your
Textbook
Rotational Kinematics
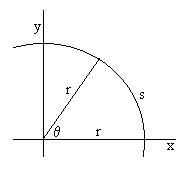
Let's consider a point mass free to move about a circle of radius
r.
First, we need to be able to specify the object's position. For
this
we will return to our convention of measuring angles CCW from the
x-axis,
however, we will for now on think of such angles in radians,
not
degrees.
A radian is the angle such that the arclength s subtended is
equal to the radius r, or about 57.3o. Clearly, if we
halve the angle, we also halve the distance along the arc, so that q
and s are proportional by the factor r:
s = qr.
So, there are then 2p radians in a circle,
since the circumference is 2pr.
We should next find a way of describing changes in the position, or
the angular displacement, Dq,
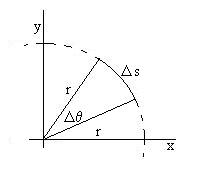
so that Ds = Dq
r.
Since linear displacement was a vector, we might want to assign a
direction
to the angular displacement as well. First, we must define the
plane
in which the rotation occurs, which we can do almost unambiguously by
picking
a vector perpendicular to that plane. However, there are two such
vectors:

Again, by convention, we'll pick one vector to represent rotation in
one direction, and the other to represent the reverse rotation.
Use
a variation of the right hand rule (RHR): curl your fingers in
the
direction of rotation, and your thumb will point in the direction of
the
vector Dq.
Then we continue with the angular velocity, the angular
displacement
per
unit time:
wave = Dq/Dt;
winstantaneous
= lim Dt ->0 Dq/Dt;
direction of w also given by RHR.
Now, the speed around the circle, the tangential velocity,
will
be vT = Ds/Dt.
We
can
see that if Ds = Dq
r, then vT = wr.
Likewise, we can define the angular acceleration as the time rate of
change of the angular velocity:
aave = Dw/Dt;
ainstantaneous
= lim Dt ->0 Dw/Dt;
direction of a also given by RHR.
Once again, we see a relationship between the angular quantity and
the
tangential quantity:
aT = DvT/Dt
= (Dw r)/Dt = (Dw/Dt)
r = a r.
If we assume that there are situations where the angular
acceleration
is constant, we can derive some kinematic
relationships. Since there is an analogy between the the
definitions
of q and s, w
and
vT, and a and aT, we
need
not actually perform these derivations, but simply replace each linear
quantity with the analogous rotational quantity:
vT = vTo + aTt
vT ave = [vTo + vT]/2
s = so + vTot + 1/2aTt2
vT2 = vTo2 + 2aT(s
-
so) |
w = wo
+ a t
wave = [wo
+ w]/2
q = qo
+ wot + 1/2a t2
w 2 = wo2
+ 2a (q - qo) |
Torque
Back in Section Four, we saw that Newton's second law says that a net
force
is necessary in order for an object to have an acceleration. We
might
expect a similar necessary condition in order for an object to have an
angular acceleration. Instead of a 'push' or 'pull,' it requires
a 'twist.' The technical term for a twist is torque.
So,
we
might guess that, in analogy with NII,
Si ti
=
I a,
where I is some measure of the object's rotational inertia (how hard
it is to accelerate rotationally) in the same way that the mass m is a
measure of its translational inertia (how hard it is to accelerate
linearly).
Before we try to justify this relationship, let's see if we can work
out exactly what the torque means. Consider an object free to
rotate
around a particular axis, such as a door about its hinges. To get
the door to begin to accelerate rotationally, it seems clear that a
force
must be applied.
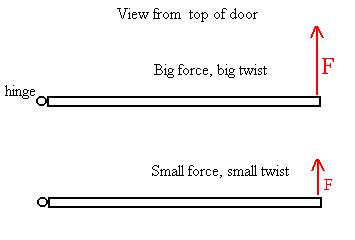
The larger the force, the bigger the twist applied. So we might
guess that
t ~ F.
Where the force is applied also seems to matter. Try pushing
the
door near the end, then with the same force near the centre. See
how the former results in more twist than the latter. Pushing
near
the hinge (axis) results in no twist at all.

So, now we might think that
t ~ Fr,
where r represents the distance from the axis of rotation to the point
of application of the force.
Lastly, we se that there is a dependence on the orientation of the
force
with respect to the door. Namely, if we pull or push along the
door,
there is no twist, and we obtain the maximum twist when the force is at
right angles to the door.
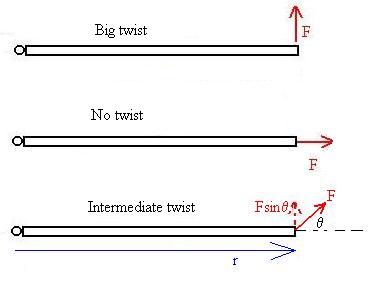
At intermediate angles, it seems clear that we need to take the
component
of the force which is perpendicular to the r-vector, namely Fsinq,
where q is the angle as shown between the
force
vector and the r vector. So, we might now guess that
t ~ F r sinq.
We also need to define a direction for the torque (after all,
we can twist a bottle cap on or off). Assuming that the door
starts
from rest in the example above, then starts to turn CCW as a result of
the applied force shown. Then, Dq is
out
of the page, wave is out of the
page,
and a is out of the page. Since for
translational
motion, the net force and the acceleration point in the same direction,
we will require the net torque and the angular acceleration to do so as
well. We see that we can get this result by defining the torque
as
the cross-product of r and F:
t = r x F
or in our notation:
|t| = r F sinqr,F
(RHR).
The magnitude of the torque is found from the formula, and the
direction
through use of the right hand rule (RHR). In this case, the
result
of the cross product is out of the page, just as we wanted.
Now, this result is still tentative, since although we know on what
factors the torque depends, we don't know the exact dependence.
Only
testing of the usefulness of this definition will vindicate our work
here.
There is no special unit for torque; it's clear then that we can
write
it in terms of newton-metres.
Occasionally, the torque will be expressed as the product of a force
and its lever arm, l.
t = Fl (RHR).
The lever arm is found by extending the line of action of the force
and finding the perpendicular distance (the lever arm) from the pivot
to
this line.
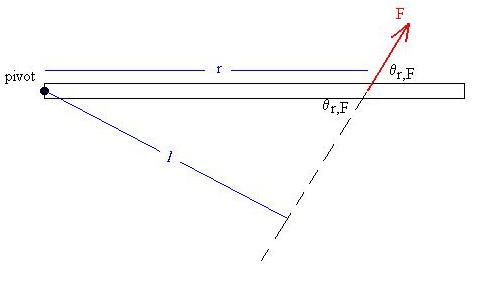
Clearly, l = r sinq, so this
definition
is equivalent to, and sometimes more useful than, the one given above.
Center of Mass
Until the discussion immediately above, we have been treating objects
as if they were point masses.
For
example, the location of a car could be given by xCAR =
34.7m, but what does that actually mean? We could mean that the
nose of the car is there, or tip of the shift lever; for displacements,
there really isn't any import to any difference. However, now we
will start to think of masses as extended
objects, and on occasion we will want to describe the average
position of the object. Now, by average position, we don't mean
the average over time, but rather the average over the object at any
given instant in time. For example, the average position of a
meter stick can be said to be at the 50cm mark, halfway into the
thickness of the wood and halfway down the side of the stick.
This position is known as the center
of mass.
The average of the grades on an exam are calculated by multiplying each
grade Gi by the number of student who earned that grade Ni,
then
dividing that sum by the total number of students:
GAVE = [Si Ni Gi
]/[Si
Ni]
The average position is found the same way. If the constituent
mases are themselves point masses, then:
xCM = [Si
mi xi ]/[Si
mi]
If the object is a continuous distribution of mass, then a similar
calculation must be done using calculus.
The center of mass has one especially remarkable property.
Consider a system of masses mi with total mass M = Si
mi:
xCM = [Si
mi xi ]/[Si
mi]
[Si
mi] xCM = Si
mi xi
M xCM = Si
mi xi
Now, that the time rate of change of each side, twice:
M vCM = Si
mi vi
M aCM = Si
mi ai
Now, let's consider all of the forces acting on
any of the masses. For each one, we have
FTOTi = miai
And if we add up all of those equations, we get
FTOT = Si
mi ai
which is of course to say that
FTOT = M aCM.
In other words, all of the forces acting on any of the parts of the
collection of masses will accelerate the secter of mass as if it were a
sungle particle of mass M.
Newton's
Second
Law
for Rotation and the Moment of Rotational Inertia
Following up on the notion of the existence of an analogy between
linear
and rotational motion, we might suspect that that there is a
relationship
similar to Newton's second law,
Si Fi = ma,
perhaps of the form
Si ti
=
I a,
where I is a constant whose meaning we still need to divine, but which
we suspect might be a measure of how difficult it is to accelerate
rotationally
some object, in the same way that an interpretation of the mass is as a
measure of the difficulty of altering an object's linear velocity.
Consider an object (point mass) constrained (for now) to move along
a circular path, to which forces are applied:

However many forces are applied, they can be added and resolved into
components which are either centripetal or tangential, resulting in net
force components like this:
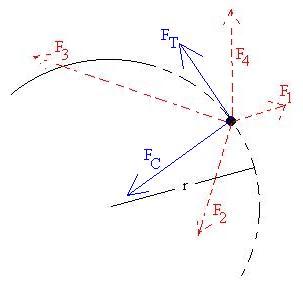
The centripetal component is what keeps the object moving in a circle,
and is of no particular interest to us just now. The tangential
component,
however, will accelerate the object along the circle, that is,
tangentially:
Si FTi = maT.
Let's multiply both sides of the relationhip by the radius, r:
[Si FTi ] r = maT
r.
Distribute the r:
Si [r FTi ] = m aT
r.
Since every tangential force component is (by definition) perpenducular
to the radius r, we recognize the terms in the sum to be the torques
exerted
by each of the forces, and we remember that
aT = a r,
so that
Si ti
=
m (a r )r = [mr2] a.
So, in this very special case, we see that a rotational form of
Newton's
second law holds true, if the proportionality constant is
Ipoint mass = mr2.
Note that this quantity depends not only on the mass, but on the
distribution
of the mass. This last comment should become clearer after the
next
discussion.
Suppose we have an object that comprises several point masses which
are somehow connected, perhaps with light rigid rods:

Without bothering to calculate each torque explicitly, we can safely
assume that there will be some torques applied to each object,
including
external torques due to the forces shown (make each the net force, if
more
than one force is desired), and also due to internal torques from the
other
objects, mediated through the rods. For each mass, we can write
that
t1 ext + t1
int = I1 a1
t2 ext + t2
int = I2 a2
t3 ext + t3
int = I3 a3
and so on.
If the objects rotate as a single object about a common axis, the all
the a 's are the same. Let's add the
equations
(three here, but there could be as many as we like...):
t1 ext + t1
int + t2 ext + t2
int + t3 ext + t3
int t = I1 a1
+ I2 a2 + I3a3
= [I1+ I2 + I3 ]a
The sum of all the internal torques should be zero, since the third
law says that each force that one mass exerts on another will match up
with a force that the other exerts on the one, which is equal in
magnitude
and opposite in direction, and because the lever arms of these torques
will be equal as well; this means that the torques are also equal in
magnitude
but opposite in direction. The sum of the external torques is
just
the sum of the torques exerted on the masses as a unit, so we now have
that
Si ti
= (Si Ii ) a,
from which we see that the moment of inertial of an extended, rigid
object is the sum of the moments of its constituent parts:
ITOT = Si Ii.
More generally, we would break an extended object (or a group of
objects
connected rigidly) into a very large number of tiny point masses, mi,
for
which
we already know that the individual moments of inertia are mi
ri2,
so that
ITOT = Si miri2.
NOTE: Because the value for the moment of inertia depends not only
on
the mass, but also on the distribution of the mass in an
object,
the value for I for a given object may well (and probably will) be
different
for different axes of rotation.
Example:
Find the moment of inertia of a hoop of radius R and mass M about an
axis passing through the centre of the hoop, perpendicular to its
plane.
IHOOP = Si Ii
= Si mi ri2
Now in this case, each piece of the mass is the same distance R away
from the axis, so
IHOOP = Si mi
R2
= [Si mi
] R2
= MR2.
Will the moment of this same hoop be greater, the same, or smaller
if it were rotated about one of its diameters?
Try this:
Pick up a metre stick at the centre and try to twist it back and
forth.
Now try the same thing, but while holding the stick near the end.
Which was harder to do?
Compare the moments of the hoop,
a disc, and a sphere, all of mass M and radius R about an axis passing
through the centre and perpendicular to the plane of the object (that
means
nothing for the sphere, of course). Try to place them in order of
decreasing moment of inertia:
Finding the moment of inertia for objects about different axes
usually
requires calculus (there is a table of common moments in your
textbook),
but there are some special cases (such as the hoop) and some useful
techniques.
The parallel axis theorem states that, if one knows the
moment
of inertia about an axis passing through the centre of mass of
an
object (ICM), then the moment about any other axis parallel
to that one is given by
I = ICM + Mh2,
where h is the distance the second axis is
displaced
from the first.
For simplicity of calculation, align the x axis
along the direction of the displacement of the axis of rotation and
place
the origin at the centre of mass.
FIGURE
The moment about the centre of mass is
ICM = Si
mi ri2 = Si
mi [xi2 + yi2]
The moment about the new axis is
I = Si
mi (ri' )2 = Si
mi [(xi - h )2 + yi2]
=
Si mi [xi2-
2hxi + h 2 + yi2]
=
Si
mi [xi2 + yi2]
+
Si
mi h 2 -
Si
mi 2hxi =
= Si mi [xi2
+ yi2] + [Si
mi] h 2 - 2h Si
mi xi
The first term we recognize as ICM,
the second is Mh2, and the third is 2h/M times the x
co-ordinate
of the centre of mass, which we specified was at the origin, so that
term
is zero.
So,
I = ICM + Mh2.
Here is an example:
The moment of inertia of a thin rod of length L and mass M, about an
axis through its centre perpendicular to its length, is found (using
calculus)
to be
ICM = 1/12 ML2.
What is the moment about an axis passing through the end of the rod,
perpendicular to the length of the rod? This fulfills the
necessary
condition for the theorm, so we can write that
IEND = ICM + Mh2 = 1/12
ML2+ M (L/2)2 = 1/12 ML2+
1/4
ML2 = 1/12 ML2+
3/12
ML2 = 4/12 ML2 = 1/3
ML2.
The perpendicular axis theorem is valid for objects which
are
two dimensional, that is, flat and with zero thickness. This
theorem
states that, by knowing the moment about each of two axes in the plane
of the object that are perpendicular to each other, we can find easily
the moment about a third axis, perpendicular to the other two that
passes
through the intersection point of those first two.
IZ = IX + IY.
Let's prove it. For simplicity of
calculation,
let the two axes in the plane of the object be the x and y axes; they
do
not
need to intersect at the centre of mass. The z axis comes out
perpendicular
to the plane of the object.
FIGURE
IX = Si
mi yi2
IY = Si
mi xi2
IZ = Si
mi ri2 = Si
mi [xi2 + yi2]
=
Si mi xi2
+ Si mi yi2
= IX + IY
Example:
Suppose that we want to know the moment about the diameter of a
hoop.
We already know the moment about an axis through the centre,
perpendicular
to the hoop:
IZ = MR2= IX + IY.
By symmetry, it's clear that IX and IY are equal,
so
IZ = MR2 = 2IX
IX = 1/2 MR2.
More examples:
Find the moment of inertia of a disc (mass M and radius R) about an
axis in the plane of the disc, passing tangentially through the rim of
the disc.
FIGURE
First, use the perpendicular axis
theorem to find the moment of inertial about a diameter; the method is
similar to that used in the preceding example. Then use the
parallel
axis theorem.
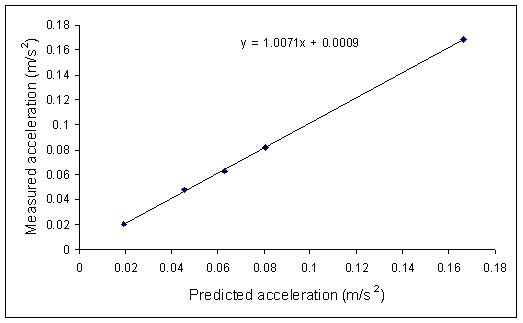
Here are the results of an experiment to verify NII for rotation.
A hanging mass pulled a string wrapped around the hub (radius r) of a
horizontal disc of moment I. The frictional torque was estimated
by allowing the mass to drop at constant speed. You derived the
expression:
aCALC = [m*ag*r - tF]/[I/r - mr]
Mastery Question
This one will be a real test for
you: Consider a thin annulus (or ring) of mass M, outer
radius
RO, and inner radius RI.
FIGURE
What is the moment of inertia about
an axis in the plane of the annulus passing tangentially to the inner
radius?
I'll post
a solution to this someday.
Rotational Kinetic Energy
Continuing with the notion of there being quantities in rotational
motion
which are analogous to quantities in translational motion, we might
expect
that there is such a thing as rotational kinetic energy, which
we
might guess has the form
KEROT = 1/2 Iw2,
since w is analogous to v and I is
analogous
to m.
Let's prove it. Consider a rigid object rotating about some
axis.
Each particle of the object, mi, will have kinetic energy by
virtue of its motion, and the total KE will be the sum of the
individual
KEs:
KE = Si1/2
mi
vi2
FIGURE
As seen from the axis of rotation, these vis are
tangential velocities, vTi. We saw previously
that
there is a relationship between the angular velocity and the tangential
velocity,
vTi = wi ri,
so we can substitute
KE = Si1/2
mi
[wi
ri]2
But all the w's are the same, since it's
a rigid body, so factor it (and the half) out of the sum:
KE = 1/2 [Simi
ri2] w2
The quantity in parentheses we recognize as the moment of inertia for
the object, and so
KEROT = 1/2 I w2
as expected. The unit of rotational KE is still the Joule.
Note that we could have thought of the kinetic
energy in the preceding example as either translational or as
rotational.
In a sense, it all depends on your point of view.
What happens when an object (mass M) is
rotating
in addition to an overall translational motion?
Each particle of mass mi
will have
a velocity vector vi, as seen by some outside
observer,
so that
KETOT = Si1/2
mi
vi2 = Si1/2
mi
(vi . vi)
Now, we can use the concept of relative
velocities
to write vi = vRA + vTi,
where
vRA is the velocity of the rotational axis and
vTi
is
the tangential velocity of mi relative to an observer
riding
along with the rotational axis.
KETOT = Si1/2
mi
(vRA + vTi ) .
(vRA + vTi ) = Si1/2
mi
(vRA. vRA ) + Si1/2
mi
(vTi . vTi
)
+ Si1/2
mi
(vRA. vTi )
KETOT = Si1/2
mi
vRA2
+ Si1/2
mi
vTi2
+ Si1/2
mi
(vRA. vTi )
KETOT = 1/2[Simi
]
vRA2
+ 1/2[Simi
ri2]w2 + 1/2
vRA.
[Simi
vTi
]
KETOT = 1/2M
vRA2
+ 1/2Iw2 +
1/2
vRA.
[Simi
vTi
]
The third term is a bit tricky to deal
with.
However, we remember that vTi represents the
velocity
vector of the ith mass relative to the axis of rotation, and
so we can write the term in the brackets as
[Simi
vTi
]
= D[Simi
ri
]/Dt
= M DrCM/Dt
= MvCM, RA,
that is, the total mass of the object times the
velocity of the centre of mass relative to the rotational axis.
So, we now have that
KETOT = 1/2MvRA2
+ 1/2Iw2 +
1/2
MvRA.vCM,RA
Now, let's consider a very common special
case,
that of an object which is translating while at the same time rotating
about an axis passing through the centre of mass. In that case, vCM,RA=
0 and vRA = vCM, so that this
reduces
to:
KETOT = 1/2M
vCM2 + 1/2Iw2
,
that is, the total kinetic energy is the sum
of the translational kinetic energy (as if the object were not
rotating)
and the rotational kinetic energy (as if the object were not
translating).
We see also that the distinction between translational KE and
rotational
KE is really arbitrary, a mere bookkeeping device for our convenience;
all KE is fundamentally translational in nature.
How do we transfer energy into or out of a
rotating
(or rotatable) object? We need to apply a net torque and do
work.
Let's derive an expression for the work done by a torque. Let's
restrict
ourselves to a two dimensional case:
FIGURE
The net force is applied a distance r from the
pivot point, and acts through a distance s, as shown. Remembering
several of the relationships we've derived so far, the work done becomes
W = Fnet s cosqF,s
= Fnet [r Dq] sinqr,F
= t Dq.
Since the torque t and the angular
displacement
Dq are both vectors, we still need to introduce a dependence on
their relative orientations so that we can determine the sign of the
work
done. Taking a hint from the work defined for linear motion,
we'll
assert that
W = t Dq cosqt,Dq.
Don't confuse
the two thetas in this relationship, they represent different angles!
The power
delivered
is then
P = t
w
cos
qt,w.
We might also be able to define a potential
energy
associated with rotation. An example is that of a torsional
spring.
Consider a wire or string which exerts a torque proportional to the
angle
through which its end has been twisted and in the opposite direction of
that angular displacement:
tSPRING
= - k Dq.
The potential
energy term might then be
PE = 1/2k
[Dq]2.
What about
the units? Well, k
is in Nm/radians = Nm (yet another quantity with the same
dimension
as energy!) and the PEROT is in (Nm)rad2 or Nm,
so
this looks O.K. dimensionally.
A special
example
of an object translating and rotating is one which 'rolls without
slipping.'
In that case, there is a relationship between the angular velocity and
the translational velocity of the centre of mass:
vCM
= Rw.
Consider
this
example:
A hoop of
mass M and radius R rests at the top of an incline (height h).
It's
released and rolls down the incline. What is the hoop's speed
when
it arrives at the foot of the incline?
Let's try
using conservation of mechanical energy. We start with potential
energy Mgh and end with none. We start with no KE and end with a
combination of translational and rotational KE:
Mgh = 1/2Mvf2
+ 1/2Iwf2.
For a hoop,
I = MR2, so
Mgh = 1/2Mvf2
+ 1/2MR2wf2.
If the hoop
rolls without slipping, we can make use of the relationship vCM
= Rw to
obtain:
Mgh = 1/2Mvf2
+ 1/2MR2(vf/R)2.
Now some
interesting
developments. First, the mass drops out, so our answer is
independent
of the mass of the hoop. Also, R drops out, so the result is
independent
of the size of the hoop.
gh = 1/2vf2
+ 1/2vf2
= vf2.
vf
= [gh]1/2.
Compare this
to the result when an object simply slides without friction down such
an
incline:
vf
= [2gh]1/2.
In this case,
the speed is lower because some of the potential energy had to go into
rotational KE, leaving less for the translational KE, and thereby
resulting
in a lower final speed.
But if it
had
been a smooth incline, the final speed of the hoop would have been vf
= [2gh]1/2. Why the difference?
Hang on, doesn't that preclude the
use of conservation of mechanical energy?
The Race:
Consider a hoop, a disc, and a solid
sphere (each with mass M and radius R) at the top of an incline of
height
h. If they are released from rest at the same time, which will
arrive
first at the foot of the incline?
We could argue that the one with
the highest final velocity will also have the highest average velocity,
and so arrive first. Review the solution above:
Mgh = 1/2Mvf2
+ 1/2Iwf2.
Since we
really
don't want to do the problem three times, let's let the moment of
inertia
be gMR2,
where g =
1 for the hoop, 1/2 for the disc, and 2/5
for the solid sphere. If the objects roll without slipping, we
can
also use vCM = Rw.
Mgh = 1/2Mvf2
+ 1/2[gMR2](vf /R)2
As expected,
the Rs and Ms cancel, leaving
gh = 1/2vf2
+ 1/2gvf2
= 1/2[1
+g]vf2
vf
= [2gh/(1+g)]1/2.
So, the object
with the highest moment (the hoop) will be the slowest and arrive last,
while the object with the lowest moment (the sphere) will arrive
first.
This should make sense, if one thinks of the fraction of the original
potential
energy each object puts into its rotational energy.
Interestingly,
any
sphere will beat any disc, which in turn will beat any
hoop.
Angular Momentum
Again as an analogy, we might suspect that there is such a thing as angular
momentum (L), and we might guess that it is defined as Iw (analogous to mv).
Let's see:
Starting from the rotational form of the Second Law,
tEXT = Ia,
substitute the definition of angular acceleration (and assume that I is
constant!) to get
tEXT = I[Dw/Dt]
= D[Iw]/Dt
tEXT Dt
=D[Iw]
= DL
The left hand side of the preceding
relationship is the rotational equivalent of impulse, and we can see
that,
in the absence of any external rotational impulses, the total amount of
angular momentum is constant, or conserved.
We can derive analogous relations
for the final angular velocities for totally inelastic 'collisions' and
for totally elastic 'collisions' by substituting moments of inertial
for
masses and angular velocities for linear velocities, although there are
some restrictions on when these will be valid (Is should be constant,
for
example!).
Two demonstrations in class:
Rotating student with
barbells.
By pulling the barbells in towards his body, he reduces the moment of
inertia.
If there are no external torques, the angular velocity correspondingly
increases. This is the same effect used by figure skaters.
Student with bicycle wheel.
A non-rotating student holds a wheel that is rotating so as to have
(say)
one unit of angular momentum, pointing upward (call this +1).
Inverting
the wheel causes the student to begin rotating. In the absence of
external torques, the total angular momentum must remain +1.
Inverting
the wheel changes its angular momentum to -1, and the student then
acquires
angular momentum +2, so that the sum remains +1. How does the
student
magically acquire just the right amount of angular momentum? Inverting
the wheel required that the student apply a torque, and so, by the
third
law, a torque equal in magnitude but opposite in direction was applied
by the wheel on the student.
Two notes on angular momentum:
First, for linear momentum, we
expected
that the masses of objects could not change, so that any changes in
momentum
p
were due to changes in velocity. For angular momentum, we see
that
a change in angular momentum can be effected by changing either
w
or I or both.
Secondly, and more interestingly,
we remember the constant, droning repetition that all three of
the
pictures we developed in linear motion (force and acceleration, work
and
kinetic energy, and impulse and momentum) were not only equally valid,
but derivable from each other. We might expect the same from the
three pictures developed for rotational motion, namely torque and
angular
acceleration, work and rotational kinetic energy, rotational 'impulse'
and angular momentum. In the classical world we are studying this
semestre this is so, but in the real world, we find the suggestion that
angular momentum is somewhat more fundamental as a concept than the
other
two. In your chemistry courses, you may have come across the
notion
that angular momentum is quantized, that is, that only certain
numerical
values are allowed; this can be true of energies also, but the values
allowed
depend on the exact system.
A Note on Rolling Objects
Often, a question arises about the effect of friction on rolling
objects.
Consider a ball rolling on a flat horizontal surface. It has
translational
kinetic energy 1/2mvCM2
and
rotational kinetic energy 1/2Iw2.
If
it
rolling without slipping, then there is a relationship between vCM
and w, namely that vCM = wR.
The friction, if any, will be static, but due to the synchonization of
the two types of motion, there is no tendency to slip, and the
frictional
force, which is only as large as it needs to be, will be zero.
But
what about an object on an inclined plane (length l )? We
discussed
in class that a rolling object will have a lower velocity at the bottom
of the plane than will a sliding object, due to the fact that the same
amount of initial potential energy is converted into both translational
and rotational energy, instead of into only translational kinetic
energy
as for the sliding object. In this case, it is the static
frictional
force which causes the object to begin to rotate in the first
place.
Let's consider the work done by Ff:
In terms of translation, the frictional force is directed opposite
to the displacement, so the work done is
Ff l cos
180o = -Ff l
.
In terms of rotation, however, the torque supplied by the the force
will be Ff R and that is in the same direction as
the
angular displacement, q. The angular
displacement
will be l/R, so that the
work done by the torque will be
W = t*Dq = +
Ff R * l/R = +
Ff
l.
So the total work done by the friction is zero. The
result
though is that some energy is 'stolen' from the translational motion
and
'given' to the rotational motion.
Mastery Question
Consider a bowling ball that is released with initial translational
velocity
vo but which is not initially rotating. Calculate the
velocity of the ball and how far down the alley it is when it begins to
roll without slipping.
Click here for a Solution.
Return to Notes Directory
Continue to Next Section of Notes
D Baum 2001