Section 1-4 - Dynamics
Newton's Laws of Motion
Weight
Normal Force of Contact
Tension
Applications of Newton's
Laws:
Some Illustrative Examples
Friction
More Example Problems
Correlation
to your Textbook
Newton's Laws of Motion
Up to this point, we have done basically no physics. All of our
work
was based on definitions and some mathematical calculations, with two
factoids
thrown in: the acceleration of a body moving under the influence of
gravity
is ag (9.8 m/s2 downward), and that the
motions
of an object in the x and y directions are independent of one another
(which
incidently is not always true). Now we shall start to discuss
the
'postulates' of physics, things which we observe never to be false and
which we then assume are true, the
laws of physics.
The root of the word dynamics comes from the greek word for force.
For the moment, we shall employ our grade school definition for force,
a push or a pull. We shall study the effects of these forces on
the
motions of objects.
The history of the study of classical mechanics is interesting and
involves
a lot of very smart people. For simplicity, certain views are
often
ascribed to one of three historical figures, whether those men actually
held those beliefs or not: Aristotle, Galileo, and Newton.
The notions students have when they start a course in classical
mechanics
are often
Aristotelian; examples include that a force is necessary
to keep an object in motion, or that a ball dropped from the mast of a
moving ship will hit the deck astern of the base of the mast.
Part
of the purpose of these classes is to disabuse students of these
Aristotelian
notions. Oddly enough, studies show that even students who have
performed
well on course exams still hold the same Aristotelian notions at the
end
of the class that they started with.
Here is the simplified history of Mechanics:
Aristotle is often credited with being the first observational
scientist.
He saw things in the world around him about which he was curious and
attempted
to explain them through logical arguments. Generally, these
explanations
were wrong, mostly because he didn't or couldn't separate out processes
which act concurrently. For example, an object's natural
motion
is to fall toward the earth and come to rest. Even if the object
were subjected to a violent motion (such as being thrown), the
natural
motion will eventually take over. This seems pretty logical,
since
one can see this behaviour daily. Another example might be to
slide
a book across the table; very soon, the book will come to a stop and
remain
at rest. Aristotle might have said something like this:
An object at rest will remain at rest unless acted on by a force.
An object in motion will come to rest unless acted on by a force.
Galileo is often called the first experimental physicist; he
actually
set up different scenarios in a lab to test his understanding of the
laws
of nature. He was the first to try to separate out the different
effects that could influence an object's motion so as to study them
independently.
For example, we all probably know what it is that makes the sliding
book
come to rest: friction. What if the table were made
smoother?
How far would the book go before stopping? And if it were
smoother
still? And if it were perfectly smooth? The book would
slide
forever. Galileo's version of these laws might have been:
An object at rest remains at rest unless acted on by a force.
An object in motion will continue that motion unless acted on by
a force.
The second part, in other words, means that an object will
maintain
a constant velocity (acceleration will be zero) unless a force acts on
it.
This last set of rules is now known as Newton's First Law of Motion.
Newton went a bit further. He investigated how those forces
altered
the motion of an object and found that the acceleration is
proportional
to the force applied and inversely proportional to the mass.
We can write this (tentatively at least) as
a a F/m, or more familiarly as F a
ma.
If we choose the correct units, we can make the proportionality an
equality. Let the force necessary to accelerate one kilogram at
one
meter/second2 be called one Newton. So,
F = ma
Since acceleration is a vector quantity, so must be force; this should
be obvious since one can discuss how hard to push and in what
direction.
Additionally, we see that the mass of an object is not just a measure
of
how much material is present, but also of how difficult it is to change
the motion of the object.
What if there is more than one force acting on an object? We
can
add the forces as vectors to find the net force, FNet
= Si Fi.
Think of these situations:
Two twin footballers push equally hard against an opponent in opposite
directions. Will the opponent accelerate? Are there forces
applied to the opponent? Is there a net force applied?
The players now both push in the
same direction. Will the opponent accelerate? How quickly?
Suppose one pushed toward the north,
while the other pushed toward the east. Would the opponent
accelerate?
How quickly? In what direction?
Our ultimate form of Newton's
Second Law of Motion is
Si Fi
= ma.
The second law can be verified using an apparatus similar to that used
in lab: measure acceleration based on kinematic measurements and
compare
to the force applied.
N.B.: Include in this sum only the forces which act on the body
under consideration.
Newton's Third Law of Motion
seems to be the one students have the most trouble with, although it
really
is the easiest to understand:
If object A exerts a force on
object B, then B exerts a force on A which is equal in magnitude but
opposite
in direction.
For the moment, we'll not try to
justify this (we will later in an indirect way), but think about this
scenario:
A speeding car A hits a parked car B; the parked car B is accelerated
forward
because of the force exerted by A, while A slows down due to the force
exerted backwards on it by B.
Two forces which fulfill this
description
are referred to as a third law pair. To be a third law
pair,
the forces must fit the description given above, e.g., A pulls
B
and B pulls back on A.
Question: A book sits on a
table. There is a gravitational force exerted on the book by the
earth (this is called the weight, see below) and a normal
force
of contact (see below) acting upward on the book from the
table.
If the acceleration of the book is zero (it's not moving), then what
can
we say about the two forces just mentioned?
Do these two forces form a third
law pair?
Weight
We mentioned above that there is a force associated with gravity, which
we shall call the weight, W. When an object is in free
fall,
the only force acting on it is W, which we know from lab causes the
object
to experience an acceleration of ag downward. Using
the
second law, we can write that
W = mag.
Since all objects will fall with this acceleration, we can see that
the ratio of W to m must be constant, or if you like, that the weight
of
an object is proportional to its mass by some factor which we'll call
g:
W = g m.
Note that g must be a vector quantity (pointing
downward).
How big is g? The fact that
W = g m = m ag
implies that numerically,
g = ag,
although the units really should be N/kg, not m/s2.
g = 9.8 N/kg downward, near the surface of the earth.
We shall refer to g as the strength of the gravitational
field.
Why go through all this? Well, suppose that I were to drop a
ball
and ask you, 'what is the acceleration due to gravity?' You'd say
9.8 m/s2 downward and be right. Now, let me drop a
smaller
ball, and ask again, then a yet smaller ball, and so on. So long
as there actually is a ball to drop, the acceleration is 9.8 m/s2
downward. But what if there is no ball to be accelerated?
What would be ag then? On the other hand, even if
there
were no ball the strength of the field would still be 9.8 N/kg.
Now instead, consider a ball resting on a table. What is the
acceleration?
Does the ball still have weight? Of course, but it has no
acceleration,
let alone an acceleration of 9.8 m/s2 downward.
This is why we need an alternate interpretation.
Also, this approach to thinking about fields will be useful when we
talk about electric fields in the next semestre.
Normal Force of Contact
There are many types of forces. One we've discussed briefly, the
attraction of two objects due to gravity. Another type of force
is
the normal force of contact, which is due to the fact that two
objects
are touching one another. These forces are called 'normal'
because
the force is perpendicular (normal) to the surface of contact.
The
nature of this type of force can be thought of as being due to the
bonds
between atoms or molecules in each of the materials. You may have
learned in chemistry that the forces between these particles looks a
bit
like this as a function of the separation:

The forces of repulsion and attraction cancel at the equilibrium
separation
(F = 0). Around this point, it can be shown that the system acts
much like balls connected by springs. So, as the two macroscopic
objects come into contact, the 'springs' are compressed and produce
forces
which act to push the objects back apart. Or the objects could be
glued together and then pulled apart, so that the 'springs' stretch and
try to pull the objects back together. In either case, the forces
are due to contact between the objects and are directly perpendicularly
to the interface between the objects.
Tension
Often, we speak of the tension in a string or rope. We'll
define the tension to be the force the string exerts on the object it's
attached to. In this course, we usually assume that the strings
are
massless and inelastic (they don't stretch). Let's make an
argument
that the tension at each end of such a string is the same as at the
other
end (except opposite in direction). Consider a rope used in a tug
of war game. The team on the right pulls to the right with force
F, and by Newton's third law, the string exerts the same magnitude
force
(the tension T at that end, by our definition) on the team.
Likewise,
the team on the left exerts a force F' on the rope, and the reaction
force
to that is the tension T' on the left end of the rope. If the
rope
is massless, any difference in applied net force would cause an
infinite
acceleration. Hence, F = F' and T = T'.
Strings and ropes are often looped over wheels. This does
nothing
more than change the direction of the tensions at the ends, so long as
the wheel is frictionless and massless. Situations where the
wheel
is not frictionless or massless will be treated later
Applications of Newton's Laws
First a note on notation. Although we were very careful in past
sections
to measure the angle always CCW from the x axis, we shall abandon that
approach at this point. Now, vectors will be written in terms of
their magnitudes and directions will be accounted for by inserting the
appropriate signs in front of the magnitudes.
Consider a man standing on a spring scale. First of all, what
does the scale actually measure?
The man's weight does not act on
the scale, the man's weight is the force of (gravitational ) attraction
between the earth and the man, and that force acts on the
man.
To keep track of the forces acting on the man, we can use a free
body
diagram, which is just an accounting tool. Draw each of the
forces
with its tail at the centre of the body under consideration (here, the
man).
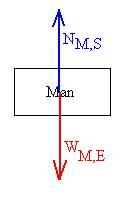
Here we see the weight (force of gavity of the earth acting on the
man) and the Normal force (force of contact of the scale acting on the
man). What about the force of the man acting on the scale?
If the man is not moving, his
acceleration
is zero, and so we can write, using the Second Law and making upward
positive,
that
Si
Fi = ma
NM,S - W = ma = 0.
or
NM,S = W = gm.
Since, by the third law, NS,M
= NM,S = mg, the
reading
on the scale is numerically equal to the weight of the man, but
it is not the weight of the man.
Now, let's put the man and the scale in an elevator which is
accelerating
upward. The diagram is similar to the one above. Writing
the
second law results in:
NM,S - W = ma
or
NM,S - gm = ma
So,
NM,S = ma + gm.
So, we see that if the elevator
is accelerating upward, the scale reading will be higher than the man's
weight, while it will be lower if the elevator's acceleration is
downward.
See Problem
4-6.
Here is a problem we shall use as
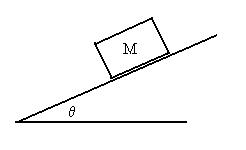
the model for presenting solutions.
Consider a block of mass M on a
frictionless plane inclined at an angle q from
the horizonal. What will be the acceleration of the block?
First, a figure may help:
Next, a free body diagram
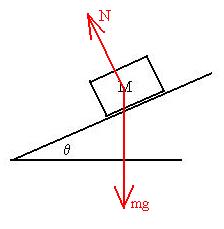
showing the forces acting on the block: first the weight which is
straight
downward, and then the normal force of contact perpendicular to
the surface. A common misconception is that the Normal force
points
upward, and is probably due to the fact that students start by trying
problems
like the first one addressed here.
Next, we'll pick a co-ordinate system. There is a need for
some
experience here, but here is a hint: we certainly expect the block to
accelerate
along the plane, and not to either jump off the plane or burrow into
it.
So, we'll try to choose a system such that the acceleration is along
one
of the axes. It will be much easier to solve this problem if we
orient
the axes parallel and perpendicular to the plane. It's not
impossible
to solve the problem otherwise, but it's a lot tougher
mathematically.
If the problem is such that the acceleration is zero, then this aspect
is not so important and other considerations need to be examined (see
below).
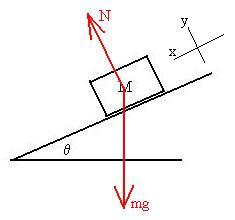
Now, we can write the Second Law as
N + gm = ma,
which is not useful, since we then have one equation with two
unknowns.
However, we saw in the last section that we can often consider the x
and
y motions separately:
Nx + (gm)x = m ax
Ny - (gm)y = m ay
In this case, Ny = N and Nx = 0. Also,
ay = 0 (see comment above) and we can let ax = a.
We must also decompose the weight:

So, (gm)x = gm sinq and (gm)y
= gm cosq.
This all leaves us with:
gm sinq = m a
N - gm cosq = 0.
It turns out that the second equation is not much use, but figuring
it out was probably good practice. Looking at the first equation
tells us that
a = g sinq.
Now, we can relate this information to other possible aspects of the
problem using the kinematic relationships discussed in earlier
sections.
In the previous example, we alluded to 'other considerations' in
choosing
a co-ordinate system. As stated, it's generally best to align the
axes so that the acceleration is along one of them; if the acceleration
is zero, this is not so important, and a judicious choice of axes might
reduce the amount of math we need to do. Consider this problem:
Apply a force horizontally to the block of the previous problem so
that
the block remains stationary. Find F and the normal force, N.
Let's start with a free body diagram:
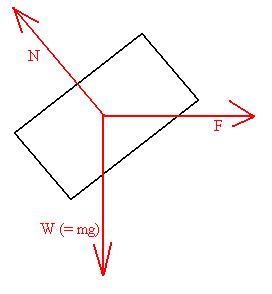
Note that the Normal force is perpendicular to the surface between
the block and the incline. Now, if one were to follow the hint
above
about choosing a co-ordinate system, one would choose the (tilted) axes
in blue in the next figure:
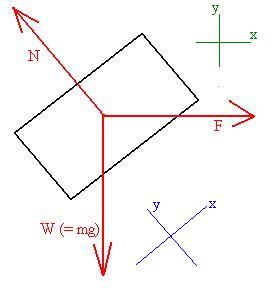
However, in this problem, the acceleration is zero ( the block is to
be held stationary). So, here is an example of those 'other
considerations.'
If one were to use the blue
co-ordinate system,
then both the Weight and Fapplied would need to be
decomposed,
giving a total of five terms to deal with in Newton's Second Law:
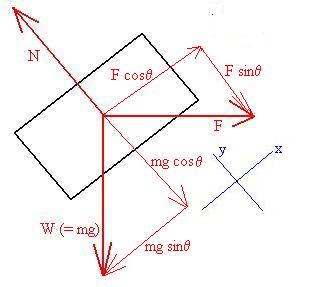
so that,
x: F cosq - gm sinq
= 0
y: N - F sinq - gm cosq
= 0
Re-arrange to get:
F = gm sinq /cosq =
gm tanq = 2*9.8*1.73 = 33.9 N
N = F sinq + gm cosq
= [gm tanq] sinq
+ gm cosq = gm [tanq
sinq + cosq] =
= 2*9.8 [0.5
+ 0.867*1.73 ] = 39.2 N
|
If one were to use the green
co-ordinate system,
then only the normal would need to be decomposed, giving a total of
four
terms to deal with in Newton's Second Law:
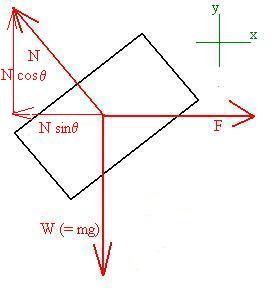
so that,
x: F - Nsinq = 0
y: Ncosq - gm = 0
Re-arrange to get
N = gm/cosq = 2*9.8/0.5 = 39.2 N
F = Nsinq = [gm/cosq]sinq
= gm tanq = 2*9.8*1.73 = 33.9 N
|
The difference in the amount of manipulation may be small, but this
serves as an example of how a judicious choice of co-ordinate systems
can
help to minimize your effort.
Let's do one more to illustrate another point:
Consider two blocks as shown with the inclined surface being
frictionless.
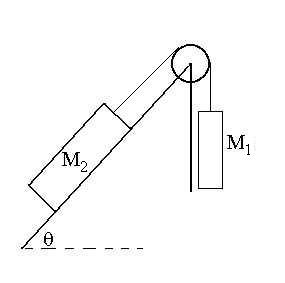
Since there are two bodies, we will have to have two free body
diagrams,
and two sets of Newton's second law equations. There looks like a
complication in choosing a co-ordinate system, though; no matter how
the
x and y axes are oriented, at least one acceleration will need to have
two components, and there will have to be several equations relating
the
accelerations of each block to each other. We can avoid this by
using
a 'fractured' co-ordinate system. For example, if mass one rises
one metre, mass two must slide down the incline by one metre (assuming
the string can't stretch). By using the system shown below,
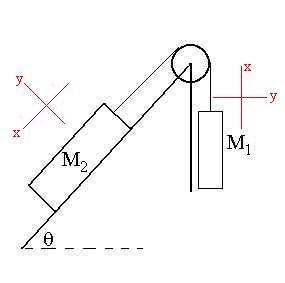
we can minimize the tedium of relating all the necessary quantities
and use simply Dx, v, and a to describe the
motions of the masses along their respective x axes, while asserting
that
there is no motion in the y directions (that is, Dx1
= Dx2 = Dx,
v1x = v2x = v, a1x = a2x =
a, v1y = v2y = 0, a1y = a2y
= 0).
Let's do free body diagrams:

Note that the angle marked q in this
diagram
is the same as the original angle of inclination.
So, write Newton's second law for each mass:
x: T - gm1 = m1ax = m1a
y: no forces
x: -T + gm2 sinq = m2ax
= m2a
y: - gm2 cosq + N = m2ay
= 0
The y equation turns out to be of no interest for this problem.
The other two equations can be subtracted to eliminate the tension
T:
| T |
- |
gm1g |
= |
m1a |
| -T |
+ |
gm2sinq |
= |
m2a |
| ---------- |
- |
---------- |
- |
------------- |
| gm2sinq |
- |
gm1 |
= |
(m1 + m2)a |
a = [(m2sinq - m1)/(m2+m1)]g
Now, to find T, we substitute this answer back into one of the original
equations. It is good form to find T such that a does not appear
explicitly:
T = gm1 + m1a = gm1 + m1[(m2sinq
- m1)/(m2+m1)]g = gm1[1 +
[(m2sinq
- m1)/(m2+m1)]
T = [m1m2g/(m2+m1)] [1
+ sinq]
Now, you can consider more difficult problems by using these
examples
as models; while the mathematical manipulations may become more
difficult,
the approach is the same.
Example:
Consider the Atwood's Machine, comprising two masses connected
by a massless string:

Find the tension in the string and the acceleration of the
masses.
Give yourself no more than one minute to obtain the correct answer.
Note the difference between 'answer' and 'solution.' The solution
would take much longer than a minute to produce.
Friction
Here is another type of force to consider. Friction
occurs
at the interface between two surfaces, and is directed along the
surface
(not perpendicular to it, as for normal forces), opposite to the
direction
in which the surfaces are sliding, or want to slide. There are
two
types of friction that we will consider: kinetic and static.
It is a common misconception that an object must be stationary to
experience
static friction, or moving to experience kinetic friction. What
is
important is whether the surfaces in question are sliding against one
another
or not; we discussed some examples in class.
We started by considering an object at rest on the desk; clearly the
sum of the forces acting on this object (weight and normal force from
the
desk) is zero, since there is no acceleration. Then we applied a
small force horizontally to the object, but we were mildly surprised
that
it did not accelerate; if Newton's second law is to remain correct,
there
must be yet another force acting oppositely to our applied force which
causes the total horizontal force to be zero (second law, Fappl
- Fmystery = ma = 0).
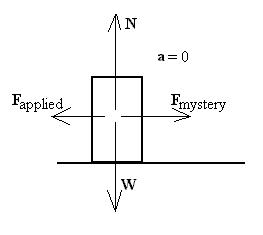
What's more, the magnitude of that force changes as we change
our applied force; it's always just big enough to cancel our
force.
That is, if we apply 2 newtons, it applies 2 newtons, if we apply 5
newtons,
it applies 5 newtons. We'll call this force friction.
A graph of this situation might look like this:
Furthermore, we saw that, if we continue to increase our applied force,
there comes a point at which this frictional force reaches a maximum
value;
we know this because we can apply enough force to make the object move,
and that requires a net force. How big is this maximum
frictional
force and what quantites determine its value?
We did a demo which should have convinced you that the magnitude of
the maximum frictional force is related to the nature of the surfaces
that
are pressed against one another, and also proportional to the normal
force
with which the surfaces are being forced together:
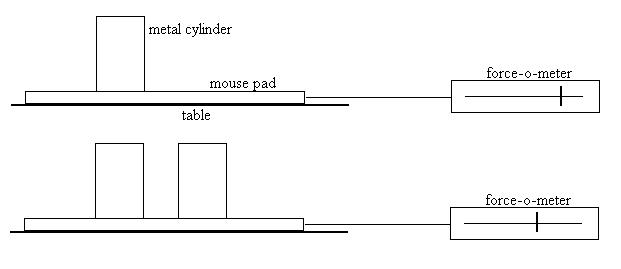
We measured the maximum value of the frictional force by attempting
to move one metal cylinder (sitting on a mouse pad 'sled') and noticing
what force was necessary to get the cylinder to start just
moving.
We repeated the experiment with two cylinders and found that about
double
the force was required. Does the maximum frictional force then
depend
on the mass of the object? Not directly: we repeated the
experiment
with my hand pushing on the mousepad and found that the force necessary
to budge the pad depended more directly on how hard I pushed down on
the
pad. In other words, the maximum frictional force really depends
on the normal force acting between the two surfaces. By doubling
the mass of the cylinders, we double the weight, double the normal
force
(second law), and thereby double the maximum possible frictional force
(If this is not entirely convincing, we could repeat the experiment
using
a magnet on the mousepad, and vary the normal force by putting various
strength magnets under the table to attract the riding magnet.).
So, we may tentatively write that
FfMAX ~ N.
Second, we flipped the mousepad over so that the shiny side was in
contact with the table and repeated the experiment. We found
again
twice as much force was required to budge two cylinders on teh mousepad
as to budge one, thus verifying the result above, but also suggesting
that
the maximum possible frictional force depends on the nature of the two
surfaces in contact. This effect is quantified with a number
called
the co-efficient of friction, m,
such
that
FfMAX = mN.
This co-efficient is usually determined experimentally, and has
different
values for different combinations of surfaces; there should be a table
of common combinations in your textbook.
To review so far:
There is a force of contact called friction which acts along
the interface of two objects (as opposed to perpendicular to the
interface,
as for the normal force of contact).
This force is only as big as it needs to be to prevent the
surfaces
from sliding against one another, but only up to a maximum value
that depends on the natures of the two surfaces and on how hard they
are
being pushed together:
Ff 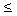 mN.
mN.
Now, what happens to the frictional force once the object starts to
move (or more properly, once the surfaces start to slide against one
another)?
It doesn't go to zero, since we know that friction will bring a book
sliding
across the table to rest. We repeated the experiment outlined
above,
making our measurements after the cylinders were already moving.
First, we made an argument that, if we drag the mousepad and metal
cylinders
at constant speed across the table, the force applied by the
string
is equal in magnitude to the frictional force (second law, Fappl
- Ff = ma = 0). We found that putting another cylinder
on the pad doubled the frictional force. Is this because the mass
is double? No, since in the absence of friction, no applied force
would be needed to keep the object moving, regardless of the mass on
the
pad. It is instead because the (vertical) normal force N has
increased
to compensate the increased weight. We tested this again by
pushing
down on the pad and sliding it across the table. We also
investigated
the effect on the nature of the surfaces by turning the pad over so
that
its rough side was in contact with the table. In the end, we
developed
this relationship, similar to that above:
Ff = mN.
We will find that, unlike the previous case, the frictional force due
to the sliding surfaces is (approximately) constant; we test this by
sliding
the apparatus across the desk at various constant speeds. We also
find that this co-efficient is generally less than the one above; think
of how much easier it is to keep a heavy object moving across the floor
than to get it to move in the first place. So we'll need to be
able
to distinguish them: the symbol mK
represents the
co-efficient of kinetic friction (surfaces are sliding),
while mS represents the
co-efficient
of static friction (surfaces are not sliding).
FSf 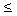 mSN.
mSN.
FKf = mKN.
Generally, mS > mK.
Because of the inequality in the relationship for static friction (the
static frictional force is only as big as it needs to be), we usually
restrict
ourselves to situations where the surfaces are 'about to slide,' or
some
similar condition so that we know that we are at the critical point
when
the equality holds true.
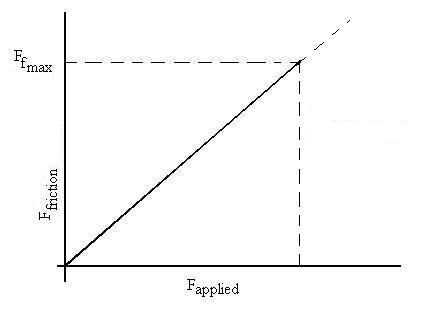
Here is a not very good figure which indicates approximately this
behaviour.
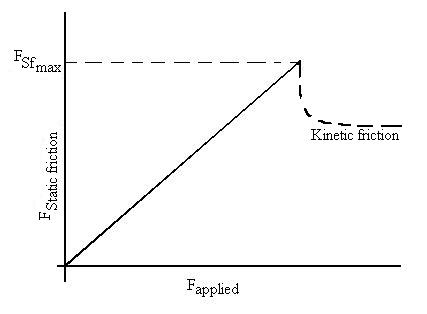
Mastery Question
Suppose that the applied force is zero, then increases toward mSN,
at which point the surfaces start to slide against one another.
Clearly,
if the force is further increased, the friction will be of the kinetic
type. What, however, will happen if the force is decreased from
the
value of
mSN after the surfaces start
to slide?
Click
here
for Solution.
Mastery Question
Suppose that a stone is tied to the ceiling with a string. An
identical string is tied to teh underside of the stone and hangs
down. Now, suppose that you pull slowly but steadily downward on
the lower string. Which string will break? If instead you
yank downward on the lower string, which string will break?
Click here for Solution.
More Example Problems
A 1000N box is kept moving with constant velocity across a floor by a
300
N force F applied at an angle of 20o below the
horizontal.
What is the co-efficient of kinetic friction between the box and the
floor?

Becuase of the wording of the problem (F keeps the box moving), we
assume that the block is moving toward the right.
Correspondingly,
the frictional force is to the left. The velocity is constant, so
all components of the acceleration are zero.
SiFi = ma
x: F cosq - Ff = max
= 0
y: - F sinq - W + N = may
= 0
Ff = mKN
In this problem, we're asked to find the co-efficient of kinetic
friction,
so it's a fairly straightforward substitution:
mK = Ff /N = [F cosq]/[F
sinq + W] = [300 cos20o]/[300
sin20o
+ 1000] = 0.26.
What are the units for the co-effiicient of kinetic friction?
Just for fun, we also find that
N = F sinq
+ W = 1102 N and Ff = F cosq
= 282 N.
Also for fun, let's suppose that boss comes along and suggests that we
pull up on the box instead of pushing down, as above.
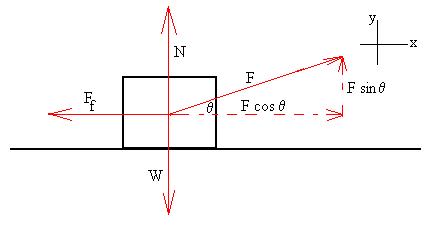
What force would be needed in this
case to keep the block moving at constant velocity, assuming that mK = 0.26?
SiFi = ma
x: F cosq - Ff = max
= 0
y: F sinq - W + N = may
= 0
Ff = mKN
Start substituting:
F cosq = Ff = mKN
= mK[W -
F sinq]
F [cosq +
mKsinq]
= mKW
F
= mKW/[cosq + mKsinq] = 0.26*1000/[cos20o + 0.26*sin20o]
= 253 N, which is less than the original 300N.
Is there some optimum angle to move this thing with minimum force?
Set dF/dq = 0
dF/dq = mKW[-sinq + mKcosq]/[cosq + mKsinq]2 = 0
So,
-sinq + mKcosq = 0
tanq = mK
Back to the original problem. For
Part B, the force F is applied
at 20o above the horizontal and we're asked to find the
acceleration,
assuming that mK
has the same value as before.

It is tempting to assert that, since
the horizontal component of F is the same as before, the acceleration
will
be the same, namely zero. Let's see:
x: F cosq - Ff = max
y: F sinq - W + N = may
= 0
Ff = mKN
Re-arranging and substituting results in
ax = [F cosq - Ff ]/m
= [F cosq - mKN]/m
= [F cosq - mK[
- F sinq + W]]/[W/g] = [300 cos20o-
0.26[ - 300 sin20o + 1000]]/[1000/9.8]
= 0.48 m/s2.
How did this happen? Take a look at N and Ff:
N = - F sinq
+ W = 897 N. Ff = mKN
= mK [-
F
sinq + W] = (0.26)(-300*sin20o
+
1000) = 233 N.
Before, the normal acted to 'balance' the weight and the downward
component
of the applied force, but here the normal is 'assisted' by the now
upward
component of the applied force. Lessening N lessens the
frictional
force.
Just for fun, let's take the second scenario and change it such that
the box is moving to the left. The second law analysis is the
same
as above, except for the direction of the frictional force (watch the
red
addition sign):
x: F cosq +Ff
=
max
y: F sinq - W + N = may
= 0
Ff = mKN
Re-arranging and substituting results in
ax = [F cosq +
Ff ]/m = [F cosq +
mKN]/m
= [F cosq +mK[
- F sinq + W]]/[W/g] = [300 cos20o+
0.26[
- 300 sin20o + 1000]]/[1000/9.8]
= 11.56 m/s2.
We see that we could have obtained this result from the results of
the last problem simply by reversing the sign of mK.
This is a useful trick.
Friction problems can be very difficult to set up, depending on what
information is given. Let's look at a fairly standard problem and
see what kinds of questions can be asked and how we might deal with
them.
Consider once again two blocks connected by a light string over a
wheel,
with one block on an incline.
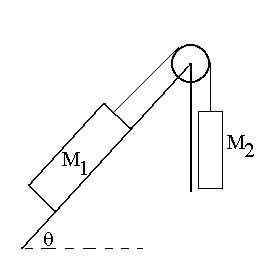
What kinds of questions could be asked? One might wonder
- what is the largest value of m1 (or the smallest value
of m2)
for which m1 will not slide down the plane?
- what is the smallest value of m1 (or the largest value
of m2)
for which m1 will not slide up the plane?
- what is the smallest value of mS
for which m1 will not slide down (or up) the plane?
- what is the smallest (or largest) value for q
for which m1 will not slide up (or down) the plane?
- what is the direction and magnitude of the acceleration, assuming
that
the blocks are in motion?
- about many things not listed here.
Many of these types of problems require us to assume or guess which way
the blocks would slide if there were no friction, since we need to be
able
to assign a direction to the frictional force which would keep that
from
happening, so often, the problem has to be solved first with m
= 0. There are a few tricks we can use, though. Let's try
some
of these questions above; luckily, most of the solutions share the
initial
steps.
Write Newton's second law, assuming that the blocks are moving, or
about
to move, with m1 sliding down the incline. Keep in
mind,
we may well be wrong about this. Even worse, the blocks may be
moving
one way but accelerating the other!
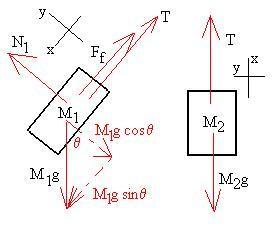
For m1,
x: - T + gm1sinq
- Ff = m1ax
y: N1 - gm1cosq
=
0
Ff = mN1
For m2,
x: T - gm2 = m2ax
y: No forces
Note that we have left the co-efficient of friction unlabelled,
since
the relationships are true for both types, so long as in the static
case,
the blocks are 'just about to move.'
Now, the only force here for which the direction is not certain is
the friction. Here though is a trick: if it turns out that we
were
wrong about the direction of Ff, we can just replace the
value
of m with its negative; this is a math
trick,
not a physics trick.
Let's address the specific questions listed above in order.
If they aren't sliding just yet, ax = 0.
- T + gm1sinq - Ff
=
0
N1 -gm1cosq
= 0
Ff = mN1
T - gm2 = 0
Through substitution and canceling out the g common to the remaining
terms, we get
m1sinq - mm1cosq
- m2 = 0.
Now, let's try to answer some of the questions posed above.
- How big can m1 be without sliding down the
incline?
Alternately,
how small can m2 be without m1 sliding down the
incline?
(m1)MAX = m2/[sinq
- mScosq
]; (m2)MIN = m1[sinq
- mScosq
]
- How small can m1 be without sliding up the
incline?
How big can m2 be without m1 sliding up the
incline?
These equations weren't written for sliding up the plane; we need to
reverse
the direction of the frictional force, so replace mS
with (-mS).
(m1)MIN = m2/[sinq
+ mScosq
]; (m2)MAX = m1[sinq
+ mScosq
]
- What is the smallest value of mS
for which m1 will not slide down (or up) the plane?
(mS)MIN = [m1sinq
-
m2]/[m1cosq].
Clearly
here the result depends on the relative sizes of the masses, such that
if the value for (mS)MIN
is positive, m1 is about (but not quite) to slide down the
plane,
while if it is negative, m1 is about (but not quite) to
start
sliding up the incline. Note that if m1sinq=m2,
then no friction is needed to keep the masses stationary.
- What is the largest (or smallest) value for q
for which m1 will not slide down (or up) the plane?
This one's tricky, involving a quadratic in sinq.
Start from result above:
m1sinq - mSm1cosq
- m2 = 0
m1sinq - m2 = mSm1cosq
m12sin2q
- 2m1m2sinq + m22
= mS2m12cos2q
m12sin2q
- 2m1m2sinq + m22
= mS2m12(1-sin2q)
m12(1 + mS2)sin2q
- 2m1m2sinq + (m22
- mS2m12)
= 0
sinq = [m2 +mS[m12(1+m2)
-m22]1/2]/[(1+mS2)m1].
Note that again, if we wanted the angle so that m1 doesn't
slide up the plane, we'd replace mS
with (-mS). We note that
this
corresponds to the other root of the quadratic equation.
If the blocks are already in motion,
- What is the direction and magnitude of the acceleration, assuming
that
the blocks are in motion?
We pretty much need to know the direction of motion in advance,
especially
since the velocity and the acceleration can certainly be in opposite
directions.
Again, assume that the blocks are sliding such that m1 is
moving
down the incline. We can still use the trick of flipping the sign
of the co-efficient of friction if the opposite is true, so that the
problem
need only be solved once.
- T + gm1sinq - Ff =
m1ax
N1 - gm1cosq
= 0
Ff = mKN1
T - gm2 = m2ax
Re-arrangement and substitution results in
ax = g[m1sinq - m2-
mKm1cosq]/[m1
+ m2]
Here's another:
Consider a car traveling down a hill inclined at angle q,
The co-efficient of static friction between tires and road is is mS.
What is the greatest deceleration the car can enjoy without skidding?
Let down the slope be the positive x-axis, so we're looking for a
negative
acceleration, here.
Write Newton's second law in each direction:
y: N - gmcosq = may = 0
x: -Ff + gmsinq = max
=
ma
Ff = mSN (in the
critical
case)
With straightforward substiution, we see that
a = [sinq - mScosq]g.
First, we see that the mass of the car doesn't matter; the answer is
the same for minis and for trucks.
Second, we see that, since we want a negative acceleration for the
car to slow, if the hill's incline is steeper than a critical value, tanq
= mS, the car will accelerate
down
the hill regardless of whether the brakes are on or not.
Conversely,
if the co-efficient of static friction is less than tanq,
the same thing will happen. What if
the
car did start to skid? Since the co-efficient of kinetic friction
is usually less than that of static friction, this would just make the
situation worse.
Another example:
Three blocks (M1 = 10 kg, M2 = 5 kg, and M3
= 3 kg) are connected by massless strings over massless, frictionless
wheels
as shown. The acceleration of the 5 kg block is 2 m/s2
to the left. The two surfaces have the same co-efficient of
kinetic
friction, mK. Find the
tensions
(T1 and T2) in the strings and the co-efficient
of
kinetic friction.
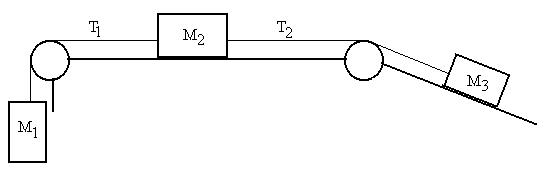
There is something wrong with the way this problem is stated.
See if you can figure it out.
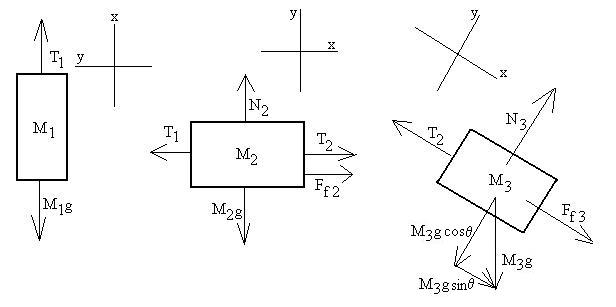
We'll assume that the blocks are sliding to the left, which I'll call
the negative x direction. Also, I'll say that all of the masses
have
the same acceleration, if I use the fractured co-ordinate system we've
discussed previously:
M1:
x: T1 - gM1 = M1a
y: No Forces
M2:
x: T2 + Ff 2 - T1 = M2a
y: N2 - gM2 = 0
Ff 2 = mKN2
M3:
x: Ff 3 - T2 + gM3sinq
= M3a
y: N3 - gM3cosq =
0
Ff 3 = mKN3
For M3, we'll solve for the Normal and substitute it in
for
Friction:
N3 = gM3cosq
Ff 3 = mKN3
= mKgM3cosq
mKgM3cosq
- T2 + gM3sinq = M3a
Let's do the same for M2:
N2 = gM2
Ff 2 = mKN2 =
mKgM2
T2 + mKgM2
- T1 = M2a
Now, let's add these two resulting equations to the one we have from
M1:
T1 - gM1 = M1a
T2 + mKgM2
- T1 = M2a
mKgM3cosq
- T2 + gM3sinq = M3a
| T1 - gM1 |
= |
M1a |
| T2 + mKgM2
- T1 |
= |
M2a |
| mKgM3cosq
- T2 + gM3sinq |
= |
M3a |
| ------------------------------------------------- |
|
------------- |
mKgM3cosq
+ gM3sinq + mKgM2
- gM1
|
= |
[M1+M2+M3]a |
This eliminated the tensions from consideration. Re-arrange to
get
mK[M3cosq
+ M2] + M3sinq -
M1 = [M1+M2+M3](a/g)
mK[M3cosq
+ M2] = [M1+M2+M3]a/g
- M3sinq + M1
mK = [[M1+
M2+ M3](a/g) - M3sinq
+ M1]/[M3cosq
+ M2]
mK = [[10
+ 5 + 3](-2/9.8) - 3sin25o+ 10]/[3cos25o
+ 5] = 0.66 (Note that, according to my co-ordinate system, the
acceleration
is -2m/s2.)
If I'd gotten a negative number for mK,
then I'd know that I'd guessed the direction of motion incorrectly.
T1 = M1 (a + g) = 10*(-2+9.8) = 78 N
T2 = - mKM2g
+ T1 + M2a = -0.66*5*9.8 + 78 + 5*(-2) = 35.7 N
Now, this really is a strange problem if we look more deeply than
the
authors intended. Why didn't we get two answers, one
corresponding
to the blocks moving and accelerating to the left, the other
corresponding
to them moving to the right and slowing down, as we normally
would?
The answer is in the specific numbers given in the problem; in the
latter
case, no friction at all gives the blocks an acceleration of -4.85m/s2,
greater than the given -2m/s2, that is, there is no
solution
for the numbers given if the blocks are sliding to the right..
Return to Notes Index
Continue to Next Section of Notes
D Baum 2000, 2002























