Let's consider a ball whirled around on the end of a string
(ignore any gravity for now). What force acts on the ball to
keep it moving in a circle?
Let's look at this situation
in more detail. Let an object move at some speed around a
circular path. Consider a particular point in the object's
path, where the velocity vector v is then tangent to the
circle. Let r
be the position vector for the object, which points from the center of the circle to
the object's location, and v is the velocity vector, which is tangent to
the circle, and therefor perpendicular to r.
r . v = 0.
Then, d(r . v)/dt =
(dr/dt) . v + r . (dv/dt) = v . v + r
. a
Now, a can have a
radial component (parallel or anti-parallel to r, positive outward) and a
tangential component (perpendicular to r): a = ar + aT, so
v . v + r
. a = v2 + r
. (ar
+ aT) = v2 + r
. ar
+ r . aT = 0.
By definition, r . aT = 0,
so
v2 = - r
. ar
.
Above, ar is the positive outward
radial component of the acceleration. The dot
product on the right side above must be negative for
v>0. Therefore, the acceleration points in toward the
center of the circle. Let's define aC as the centripetal (towards the
center) component, positive when toward the center,
such that
v2 = r aC.
Then, aC = v2/r.
So, in short, an object moving about a circular path has an
acceleration component that points toward the centre of the circle
(centripetal) for which the magnitude is v2/r.
What causes this acceleration? There must be some force or
forces which have a net component in the direction of the centre
of the circle:
Sn (Fn)C
= maC = mv2/r.
Forces which act away from the centre of the circle should be
assigned a negative sign in the sum.
Forces or components of forces perpendicular to the line
connecting the object to the centre of the circle are referred to
as tangential forces or components, for which we can write
Sn
(Fn)T = maT.
The meaning of this will be clearer after a later discussion.
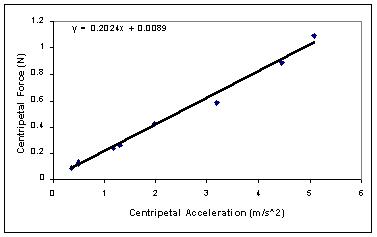
In lab, you did an experiment to verify the centripetal force
relationship above. The speed of a pendulum bob was measured
at the lowest point in its swing, while the tension in the string
was measured simultaneously with a force transducer. Here
are some results from this experiment, in which the net
centripetal force is plotted against the centripetal acceleration;
the slope should be the mass (0.2 kg in this trial, so the results
are off by 1%):

Let's return briefly to the derivation above. What if the
speed of the object had not been constant? Two things:
We would have had to replace the step,
s/Dt is the speed, v, of the object,
with
lim Dt->0 [Dr/Dt] = lim Dt->0 s/Dt=
vinstantaneous.
Also, there would had had to have been a component of the
acceleration along the direction tangent to the circular path,
which we would then have called the tangential acceleration.
But, there would still have been a centripetal component as
described.
One last note: occasionally, problems are given using the angular
velocity, w. This is the number
of radians per second (Dq/Dt) through which the object travels about
the centre of the circle. Since the arclength is given by
s = rq,
then the tangential speed is given by
v = Ds/Dt =
D[rq]/Dt = rDq/Dt = rw,
so that
aC = v2/r = w2r.

Consider
a coin on a moving turntable. What must be the minimum
co-efficient of static friction (for a given speed and radius
from the spindle) in order that the coin not slide off?
Align the
axes so that the x-direction i stoward the centre of the
circular path of the coin, and the y-direction is vertically
upward.
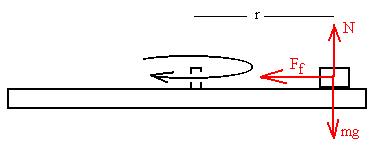
Write
Newton's second law:
SnFn= ma.
FN - mg = may = 0
Ff = max = maC = mv2/r.
Ff = mSFN
(in the critical case of the coin just about to slide).
Through substitution (not shown here) and cancellation of the mass
from each side in the result, we obtain:
(mS)MIN = v2/gr.
So, the mass of the coin doesn't matter (dime or half-dollar), and
consistent with our experience, the coin is more likely to slide
at greater speeds and at smaller radiuses.
The same results are applicable to a car driving in circles on a
flat parking lot; the static friction between tires and road
provide the centripetal force. If the car attempts to make a turn
at too high a speed, or with too tight a radius of curvature, it
will begin to skid to away from the circle's centre.
How do highway engineers minimize the necessity of friction for
turning cars along bends in the road?
D Baum 2000