Section 1-7 - Impulse & Momentum
Yet Another Picture
Impulse
Elastic
and
Inelastic Collisions
Two Dimensional
Collisions
Mastery Question
Correlation
to your Textbook
Yet Another Picture
We've looked at the motions of objects using two outwardly different,
but
ultimately identical, points of view: forces and accelerations, and
work
and energy. We know that they are the same, since we derived the
work-energy theorem using Newton's Second Law and a couple of
definitions.
Now, we'll introduce yet another picture (hence the zippy title of this
section) which we may, or may not, find convenient to use on certain
classes
of problems.
Consider two objects moving in one dimension, each with its proper
initial
velocity:
We'll let the directions of the various vectors be represented by the
signs of those quantities, just like we did back in Sections 2 &
3.
The figure not withstanding, the velocities could be in either
direction.
Suppose that these objects collide; we certainly would expect the
motions
of each mass to change due to the force exerted on it by the other.
From the Third law, we know that these forces are equal in magnitude
and opposite in direction:
F1,2 = - F2,1
Now, let's make use of the Second Law to see
the results of each of these forces on the corresponding mass:
F1,2 = m2a2
= - F2,1 = - m1a1
m2a2 = - m1a1
Remember the definition of acceleration? Substitute it in:
m2 (Dv2/Dt2)
= - m1(Dv1/Dt1)
What can we say about the two time intervals?
So,
m2 Dv2 = - m1Dv1
Let's write this out more explicitly:
m2 (v2f - v2o) = - m1(v1f
- v1o).
Now, we have a physics moment! We saw in the last section that
there was a quantity (in the absence of non-conservative forces,
anyway)
of which we had the same total amount before and after something
happened.
Might this be another example? Let's re-arrange:
m1v1o + m2v2o = m1v1f
+ m2v2f
This is very nice. Whatever this quantity mv is, we have
the same total amount before the collision as after it. This may
be useful. Let's give the quantity mv its own name, momentum:
p = mv.
In analogy with our discussion of the conservation of mechanical
energy,
we can now talk about the conservation of total momentum of a
system
of objects. Momentum may be transferred from one of the objects
to
the other during the collision, but the total amount remains constant.
Our derivation was for a one dimensional problem. However, we
could add a subscript x to each of the quantities above, then repeat
the
derivation for the y-components and again for the z-components, and we
would see that momentum is conserved independently in each of the
three
dimensons.
Note that, as we said above, the whole notion of the conservation of
momentum is nothing more than a re-statement of Newton's Second and
Third
Laws of Motion.
As an aside, we can now verify Newton's Third Law (remember that we
skipped on that in Section 4) indirectly by verifying the conservation
of total momentum, as you will do in Lab.
Impulse
Let's look back once again to the conservation of mechanical energy;
there
was a problem in that the total amount of mechanical energy was not
conserved when there were non-conservative forces present. Could
there be such a situation for momentum?
Consider the collision above, except that we shall add in an external
force, due to the action of an object outside of our system of
masses:
Let's repeat the calculation from the first section with this force
(on m1, let's say) included:
Fext + F2,1 = m1a1
F1,2 = m2a2
Remember the Third Law:
F2,1 = - F1,2
so that
m1a1 - Fext = - m2a2
Substitute as before:
m1(Dv1/Dt)
- Fext = - m2(Dv2/Dt)
m1Dv1 - FextDt=
- m2Dv2
m1(v1f - v1o) - FextDt=
- m2 (v2f - v2o)
FextDt = m1(v1f
- v1o) + m2 (v2f - v2o)
FextDt = m1v1f
- m1v1o + m2 v2f - m2v2o
FextDt = Dp1+Dp2
= Dptotal.
Since it doesn't matter which was
mass 1 and which was mass 2, this works for any situation. The
quantity
on the left we will call the impulse, the force times the time
interval
over which it was applied:
J = FDt,
so that
J = Dptotal.
What is the force is not constant in time? Analogously with the
work, we must write an integral: J
= / F
dt.
Let's review the three pictures:
- The velocity of an object will remain constant unless the object
is
acted
on by a force, in which case Ftot = ma.
- The kinetic energy of an object will remain constant unless the
object
has work performed on it, in which case Wtot = DKE.
- The momentum of an object will remain constant unless the object
is
acted
on by an impulse, in which case Jtot = Dp.
These last two we can re-write for systems of objects:
- The total mechanical energy of a system will remain constant
unless the
system has work performed on it by non-conservative forces, in which
case
WNC = DEtot.
- The total momentum of a system will remain constant unless the
system
is
acted on by an external impulse, in which case Jext
= Dptot.
Incidentally, there is a fourth picture that is very useful when the
path of an object must be determined, but we will ignore that picture
in this class.
Completely
Elastic
and
Completely Inelastic Collisions
We can define a completely inelastic collision as one in which
the
objects stick together after the collision. Let's consider a
simple
situation in one dimension in which there are no external forces (that
is, the only forces are those that each object exerts on the other):
m1v1o + m2v20 = m1v1f
+
m2v2f
Let's simplify by assuming that one object was initially at rest (We'll
learn a trick later about how to deal with situations in which both
objects
are moving), and since the objects stick together, the final velocities
are the same:
m1v1o = m1vf + m2vf
= [m1+ m2]vf
So,
vf = [m1/(m1+ m2)] v1o
Now, once again, this result will only be valid if m2 were
initially at rest.
Is kinetic energy conserved here?
(KEtot)o = 1/2 m1
v1o2
(KEtot)f = 1/2 (m1
+ m2) vf2 = 1/2
(m1 + m2) [[m1/(m1+ m2)]
v1o]2 = 1/2 m1 v1o2
* [m1/(m1+ m2)] < 1/2
m1 v1o2
No, some was lost, probably to sound, deformation of the objects,
thermal
energy, et c.
Now, let's consider a totally elastic collision, in which no
kinetic energy is lost during the collision (although, it can be
transferred
from one object to the other). We should write one equation
representing
conservation of momentum (in one dimension only) and another
representing
the fact that the kinetic energy is the same before and after.
N.B.: There is a shorter, but perhaps much less revealing, solution at
the end of this section (see One
Last Note):
m1v1o + m2v20 = m1v1f
+
m2v2f
1/2m1v1o2 +
1/2m2v202
= 1/2m1v1f2+ 1/2m2v2f2
Once again, let's let one object start at rest, just to make the math
easier:
m1v1o = m1v1f + m2v2f
1/2m1v1o2 =
1/2m1v1f2
+
1/2m2v2f2
Now, take a really deep breath.
In the second equation, we can multiply through by 2 to get:
m1v1o2 = m1v1f2+
m2v2f2
and in both equations, we can divide through by m1 to get:
v1o = v1f + (m2/m1)v2f
v1o2 =v1f2 +
(m2/m1)v2f2
To lessen the amount of writing we have to do, let's let g
represent the ratio of the masses: g = m2/m1,
so
that
v1o = v1f + g v2f
v1o2 =v1f2 +
g
v2f2
Now, we're ready to start. Solve the first equation for v1f
v1f = v1o - g v2f
and substitute into the second equation:
v1o2 = [v1o - g
v2f]2+
g
v2f2
Write more explicitly the square:
v1o2 = v1o2 -
2g v1ov2f + g2v2f2+
g
v2f2
Subtract v1o2 from each side:
0 = - 2g v1ov2f
+ g2 v2f2
+
g
v2f2
Factor out a gamma
0 = - 2 v1ov2f
+ g v2f2 +
v2f2
and a v2f :
0 = [- 2v1o + (g
+ 1) v2f] v2f
This quadratic equation has one obvious solution: v2f =
0. Let's look for the other solution after dividing out the (now
assumed non-zero) v2f:
0 = - 2v1o + (g
+
1) v2f
v2f = 2v1o/(g + 1)
Remember that g = m2/m1,
so
v2f = 2v1o/[(m2/m1)
+ 1] = [2m1/(m1
+ m2)]v1o
Let's go back and find v1f in each case:
| If v2f = [2m1/(m1
+ m2)]v1o:
m1v1o = m1v1f + m2v2f
m1v1f = m1v1o- m2v2f
m1v1f = m1v1o- m2[2m1/(m1
+ m2)]v1o
v1f = v1o - m2[2/(m1
+ m2)]v1o
v1f = v1o [1
- [2m2/(m1
+ m2)]]
v1f = v1o [(m1
+ m2)/(m1 + m2)
- [2m2/(m1
+ m2)]]
v1f = v1o [(m1
+ m2) - 2m2]/(m1
+ m2)
v1f = [(m1
- m2)/(m1
+ m2)]v1o
|
| If v2f = 0:
m1v1o = m1v1f + m2v2f
m1v1f = m1v1o- m2v2f
m1v1f = m1v1o
m1v1f = m1v1o
v1f = v1o
Which, as we indicated above, would
correspond to no collision taking place.
|
Once again, remember that these solutions are only valid if one mass
had been initially at rest, the collision was totally elastic, and
motion
was restricted to one dimension. To be clear, you should label
whichever
mass was not initially moving mass two.
What if neither mass had been at rest? Well, we could go back
and re-do the derivation with the two extra terms, but here is a neat
trick:
we can always pick a new frame of reference (indicated below by
a prime) in which v2o' is zero, then calculate the final
velocities
in that frame, then convert back to the original frame, all using
relative
velocities.
Example:
Find the final velocities of the masses given for this initial
condition.
In one dimension, letting the signs of the velocities represent the
directions:
m1 = 5 kg m2 = 2
kg
v1o = 5 m/s v2o = - 6 m/s
Let's make a chart:
|
vo |
convert to new frame
in which v2o' = 0 |
vo' |
vf' |
convert back to original frame
by reversing the previous
transformation |
vf |
| m1 |
+5 m/s |
add 6 |
+ 11 m/s |
v1f' =[(m1
- m2)/(m1
+ m2)]v1o' =
=
[(5 - 2)/(5
+ 2)]11 = 4.71 m/s |
subtract 6 |
- 1.29 m/s |
| m2 |
- 6 m/s |
add 6 |
0 m/s |
v2f ' = [2m1/(m1
+ m2)]v1o' =
=
[2*5/(5
+ 2)]11= 15.7 m/s |
subtract 6 |
9.71 m/s |
Just FYI, here are the actual solutions (asserted without proof)
which
would be obtained by solving the two equations without assuming v2o
= 0:
v1f = [(m1 - m2)/(m1 +
m2)]v1o + [2m2/(m1 + m2)]v2o
v2f = [2m1/(m1 + m2)]v1o
+ [(m2 - m1)/(m1 + m2)]v2o
Someday, when I have more interest, I'll show how this answer is
equivalent
to the method we used.
Here is an additional interesting derivation for a totally elastic
collision. Here, we do not need to assume that m2 is
intially at rest.
m1v1o + m2v20 = m1v1f
+
m2v2f
1/2m1v1o2 +
1/2m2v202
= 1/2m1v1f2+ 1/2m2v2f2
Rearrange each:
m1v1o - m1v1f =
m2v2f - m2v20
=> m1(v1o - v1f)
= m2(v2f - v20)
m1(v1o2 - v1f 2)
=
m2(v2f 2 - v2o2)
=> m1(v1o - v1f
)(v1o + v1f ) = m2(v2f
- v2o)(v2f + v2o)
Now, divide the second equation by the first:
v1o + v1f = v2f
+ v2o
and rearrange again to get:
v1o - v2o = -(v1f
- v2f).
That is, the realtive velocity of the masses before the collision is
the negative of the relative velocity after the collision. Let's
check
our example from earlier. Before the collision, the realtive
velocity
was
5 - (-6) = 11 m/s.
After, it was -1.29 - 9.71 = -11 m/s.
Now, generally, I have not found this relationship to be much
use.
It can however easily be used as a quick check on the accuracy of the
first method we worked out.
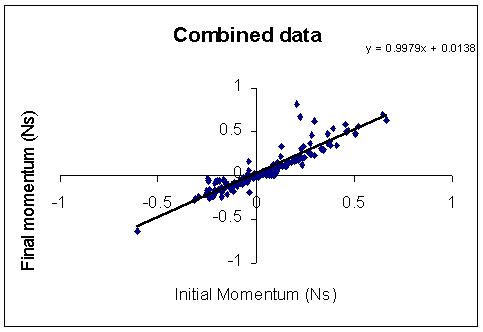
Let's try an experiment to verify the conservation of linear momentum,
and by doing so, confirm Newton's Third Law. Here are results of
total final momentum v. total initial momentum for the Post-bac
Class of 2003. Note that, even though there are a number of
outlying
points, the trend is for pTOTo = pTOTf.
Two Dimensional Collisions
As stated above, momentum is conserved in the absence of external
forces
in each dimension (x, y, or z) independently. Unfortunately, even
for totally elastic collisons, we can not make use of the results
above,
since they assumed that the speeds used to calculate the KE and the
velocities
used to calculate the momentum were the same, when in fact for two
dimensions,
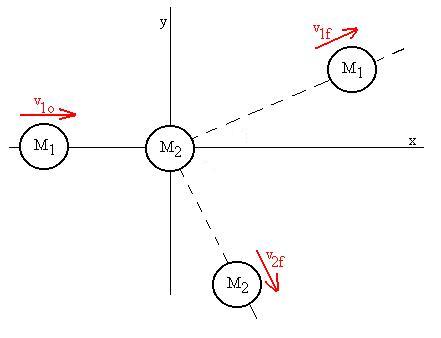
we need to worry about components. Here are some suggestions:
- Try to find a frame of reference (see above) for which one mass
is
initially
at rest; we've already seen the benefit of such a transformation.
- Try to pick a co-ordinate system in which the initial momentum of
the
other
mass is along one of the axes (say the x-axis), so that no components
will
be necessary, i.e., v1ox = v1o and v1oy
= 0.
Then,
x: m1v1o + 0 = m1v1fx +
m2v2fx
y: 0 + 0 = m1v1fy - m2v2fy.
I'll let the signs in front of the terms reflect their directions.
Now, assuming that we know all initial conditions, is this enough
information
to find the final velocities?
What if I said that the first mass
moves off at an angle q1
from the x-axis and that the second mass moves off at q2?
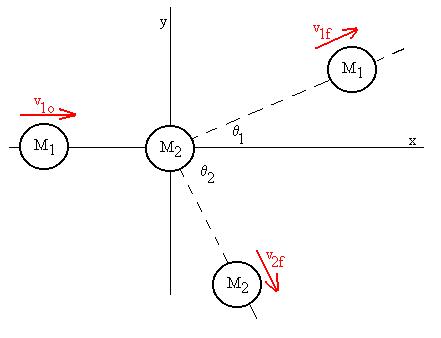
Then, I could write
x: m1v1o + 0 = m1v1f cosq1+
m2v2f cosq2
y: 0 + 0 = m1v1f sinq1
- m2v2f sinq2.
Can we solve now?
What do I need to solve?
The actual values of the angles are determined by the impact
parameter,
which describes how 'head-on' the collision is. Think of a cue
ball
hitting a pool ball; the final direction of the hit ball can be
adjusted
by the player by causing the collison to occur at slightly different
spots
on the balls' surfaces.
Here are a couple of interesting special cases (which both assume no
rotation of the objects):
Totally inelastic collision:
Since the objects stick together, vf1 = vf2 (call
them just vf ) and q 1=
q2
(call the angle just q).
x: m1v1o = m1vf cosq
+
m2vf cosq
= (m1 + m2) vf cosq
y: 0 = m1vf sinq
+ m2vf sinq
= (m1 + m2) vf sinq.
O.K., so the second relationship
implies that q
= 0, which simplifies the first to
m1v1o = (m1 + m2) vf
so that
vf = m1v1o/(m1
+ m2)
No surprise there, it's become an
essentially one dimensional problem again.
Now try a totally elastic
collision:
x: m1v1o = m1v1f cosq1+
m2v2f cosq2
y: 0 = m1v1f sinq1
- m2v2f sinq2.
In addition, we have conservation
of kinetic energy:
1/2m1v1o2 =
1/2m1v1f2
+
1/2m2v2f
2
You might imagine that this will not be easy to solve (you'd be
right!).
Let's look at a very specific case, that of the masses being equal
(mass
two is still initially at rest):
v1o = v1f + v2f
(masses cancel)
v1o2 = v1f2 + v2f
2
(halves
and masses cancel)
where I've written the momentum equations in vector form. The
first equation says we can make a figure like this:
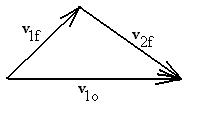
and the second, which looks a lot like the Pythagorean theorm, is only
going to be true if the triangle is a right triangle so that vif
and v2f are at right angles to one another, a nice
result.
Three Dimensional Collisions
One can imagine how difficult these might be to calculate.
However,
in the case of only two objects, we can reduce the problem to a simpler
two-dimensional case. First, move to a new reference frame in
whch
one mass is initially at rest. Then, place the x-y plane so that
it contains the two final velocity vectors. Since the z-component
of the final momentum is now zero, we know that the initial component
is
also zero, and so the initial velocity vector of mass one also lies in
that plane. Then, as above, choose the x- and y-directions so
that
the initial y-component of p is zero.
Collisions of three or more objects are not treatable this way, since
the final velocity vectors may not lie all in one plane.
Example:
S&F 6-47
A 0.5 kg block is released from rest at the top of a frictionless,
curves
track 2.5 metres above the top of a 2 metre high table. At the
bottom
of the track, this mass collides elastically with a 1 kg mass that is
initially
at rest.
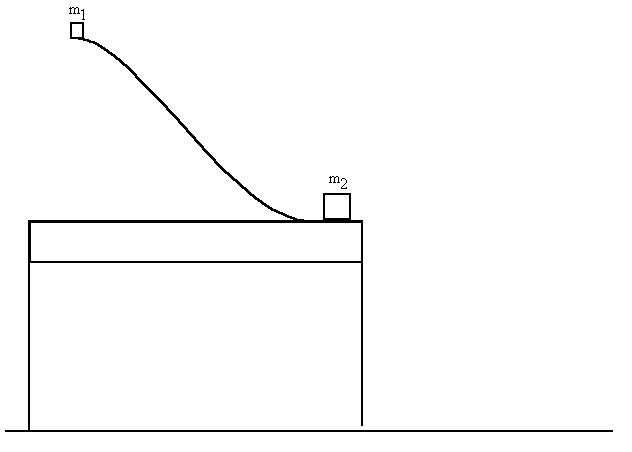
a) Find the velocities of the two masses immediately after the
collision.
b) How high back up the track does the 0.5 kg mass rise?
c) How far from the base of the table does the 1 kg mass land?
d) How far from the base of the table does the 0.5 kg mass land?
This is a good problem, in that it requires you to choose which of
the
three 'pictures' we have developed to use in each section. Keep
in
mind that the three pictures are essentially identical, but that one
may
be much more convenient to use that the other two in a given situation.
Mass one starts from rest (label situation A) and slides down the
incline
until just prior to collision with mass two (call this B). We
choose
to use conservation of mechanical energy in this case, since there are
no non-conservative forces doing work (The normal force from the
incline
is perpendicular to the direction of motion, and the weight can be
converted
to a PE term. We don't want to use impulse-momentum, since both
of
those forces are enternal and provide an impulse, the normal in a
complicated
way, and we would still need to find the time to travel down the
incline).
PEA + KEA = PEB + KEB
m1gh1 + 0 = 0 + 1/2m1v1B2
where I have set PE=0 at the table top.
v1B = 7 m/s (I will omit numerical calculation steps
in this example)
For the collision (B refers to just before, C refers to just after),
we will use a combination of conservation of momentum (no external
forces
acting horizontally, no net force vertically) and, since the collision
is elastic, conservation of kinetic energy:
m1v1B + 0 = m1v1C + m2v2C
1/2m1v1B2 +
0 = 1/2m1v1C2 +
1/2m2v2C2
We already worked out the solution to these equations (for m2
initially at rest):
v1C = [(m1-m2)/(m1+m2)]v1B
= - 2.3 m/s
v2C = [2m1/(m1+m2)]v1B
= + 4.67 m/s.
Let's look at what happens with mass two, which is now launched
horizontally
off the table. The quickest way to approach this is with the
kinematic
equations:
Dy = voyt + 1/2ayt2
= 0 - 1/2agt2
=>
-h2 = -1/2agt2
=>
t = 0.64 sec
Dx = voxt + 1/2axt2
= v2Ct + 0 = 2.99 m from the base of the table.
I've skipped on some of the background justification here too.
To find the altitude to which the smaller mass rises again on the
incline
(label this event D), use once again conservation of mechanical energy:
1/2m1v1C2 +
0 = m1ghD + 0
hD = 0.27 m
Mass one now slides back down the plane to the bottom (label this E);
find this speed once again with conservation of mechanical energy:
m1ghD + 0 = 0 + 1/2m1v1E2
v1E = +2.3 m/s (we have to add the sign ourselves after
we take the square root to indicate that mass one moves to the right).
Then, mass one is launched horizontally, so use the same relationships
as above:
Dy = voyt + 1/2ayt2
= 0 - 1/2agt2
=>
-h2 = -1/2agt2
=>
t = 0.64 sec
Dx = voxt + 1/2axt2
= v1Et + 0 = 1.49 m from the base of the table.
Center of Mass
The center of mass of an object can be thought of naively as the
average location of an extended object or collection of individual
objects. Why does this help us? We will see that the motion of the
center of mass is the same as the motion of a point particle of the
same mass were all of the external forces acting on the extended system
applied to it.
First, define the center of mass:
rCM = [Si mi ri]/[Si mi]
=
[Si mi ri]/mTOT
Now, we'll go in two directions here.
The momentum of the entire system is
pTOT = Si pi
= Si mi vi = Si
mi dri/dt = d/dt[Si mi ri] = d/dt[mTOT
rCM] = mTOT
drCM/dt = mTOT vCM.
So, the momentum of the collection of objects (or parts of an object)
is the same as is the entire mass mTOT were moving at vCM.
Second, the sum total force acting on the individual objects (or parts
of an object) is
FTOT = Si Fi
= Si mi ai
Si FEXTERNAL + Si FINTERNAL
= Si mi d2ri/dt2 = d2/dt2[Si
mi ri] = d2/dt2[mTOT rCM] = mTOT d2rCM/dt2 = mTOT aCM.
From NIII, we know that all of the internal forces will cancel, so
Si FEXTERNAL =
mTOT aCM.
Rockets
Consider a rocket of mass m out is space where there are no
gravitational effects. The rocket is moving with velocity v
relative to some observer (vR,O) when it expells a small
amount of material (- dm,
probably burnt fuel; dm is
the change in the mass of the rocket, so -dm is a positive number) out the
back at velocity vF,O.
The relative velocity (see Section 3 of these notes) of the rocket and
the fuel (vF,R) is then:
vF,O = vF,R + vR,O.
Before the fuel is expelled, the momentum of the system is:
mvR,O
and after:
(m + dm)(vR,O + dvR,O) + (-dm)vF,O
In the absence of external forces, these two should be equal:
mvR,O = (m + dm)(vR,O
+ dvR,O) + (-dm)vF,O = (m + dm)(vR,O + dvR,O) + (-dm)(vF,R + vR,O).
Let's multiply the right hand side out and cancel any terms we can (the
product of the two differential terms is very small)
mvR,O = mvR,O + dm vR,O + m dvR,O
+ dm dvR,O + (-dm)vF,R + (-dm)vR,O.
0 = m dvR,O
+ (-dm)vF,R.
Now, let's change our notation to match most textbooks. The
velocity of the rocket vR,O we'll make just plain v, and the
absolute value of the (negative) velocity of the spent fuel relative to
the rocket vF,R we'll call vEXH.
m dv = - vEXH
dm.
Now, we can go two ways with this to find out two separate
quantities.
1) m dv = - vEXH
dm
Divide both sides by dt
m dv/dt = - vEXH dm/dt
But, dv/dt is the acceleration of the
rocket:
ma = - vEXH dm/dt
and, since the only force acting on the rocket is
from the escaping exhaust, the left hand side is equal to that force
(called the thrust):
FTHRUST = - vEXH dm/dt,
where
we remember that vEXH is a positive number and that dm is a negative number.
2) m dv = - vEXH
dm
dv =
- vEXH dm/m
Intergrate each side:
vo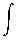 v dv =
- vEXH
mo
v dv =
- vEXH
mo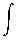 mdm/m
mdm/m
vf - vo = - vEXH ln
m/mo = vEXH ln mo/m
vf = vo + vEXH ln
mo/m
where we remember that vEXH is a positive
number.
Note:
There are three possibilities, even if there are the same
number
of equations as variables: a unique solution, an infinite number of
solutions,
or no solution. If we assume that the problem is a physical one,
i.e.
it models an actual system, our experience assures us that there will
be
a unique solution to the problem.
As an aid to visualizing these three cases, consider the equations
of two lines
in the x-y plane:
ax + by = c
dx + ey = f
A solution of (x,y) for the pair corresponds to a point of
intersection
of the lines. If the lines are parallel and separated, there is
no
solution. If the lines are parallel and lie atop one another,
there
is an infinite number of solutions. If the lines are not
parallel,
there is one solution.
Another Note:
I've been asked several times about work as measured in different
frames
of reference. I imagine that similar questions about impulse will
come soon. Let's take a look:
In 1-d; let the sign of each quantity indicate the vector's
direction:
Consider a solitary force F acting over a displacement Dx.
The work done will be
W = FDx = 1/2mvf2
- 1/2mvo2.
Now, let's write the same expression in a new frame of reference
moving
with velocity vR relative to the first frame:
W' = FDx' = 1/2mvf'2
- 1/2mvo'2.
Keep in mind that:
v' = v + vR and Dx'
= Dx + vRDt,
where
Dt is the time interval (the same in
both
frames, at least in our Galilean transformation) over which the force
is
applied.
So, immediately, we can see that the amounts of work done by the
same
force as viewed in the two frames of reference are different:
W = FDx
W' = FDx' = F[Dx
+ vRDt] = FDx
+
FvRDt = W + FvRDt
This then means that the change in kinetic energy is different in
each
of the frames, as we can see explicitly below:
DKE = 1/2mvf2
- 1/2mvo2.
DKE' = 1/2mvf'2
- 1/2mvo'2 = 1/2m[vf
+
vR]2 - 1/2m[vo+
vR]2 = 1/2m[vf2+
2vfvR + vR2] - 1/2m[vo2
+
2vovR + vR2] =
= 1/2mvf2
- 1/2mvo2 + 1/2m[2vfvR
- 2vovR ] = DKE
+ m[vf - vo]vR.
Does this make sense? Subtract the two relationships:
W' - W = FvRDt = DKE'
- DKE = m[vf - vo]vR.
FvRDt = m[vf
- vo]vR.
Divide by vR, assuming it's not zero:
FDt = m[vf - vo]
= Dp.
This is our impulse relationship. The impulse is the same in
each of the two reference frames:
Dp' = mvf' - mvo'
= m[vf + vR] - m[vo + vR] =
mvf - mvo =Dp.
One Last Note
Let's try a different solution for the case of a 1d totally elastic
collision with m2 initially at rest. We had
m1v1o = m1v1f + m2v2f
1/2m1v1o2 =
1/2m1v1f2
+
1/2m2v2f2
The first equation becomes
m2v2f
= m1v1o - m1v1f = m1(v1o
- v1f) *
and the second becomes
m2v2f2
= m1v1o2 - m1v1f2
=
m1(v1o - v1f)(v1o + v1f).
Now, divide the second equation by the first:
v2f
= v1o + v1f **
Let's next substitute this result into the starred equation:
m2(v1o + v1f)
= m1(v1o - v1f)
Rearrange:
(m2 - m1)v1o = - v1f (m1
+
m2)
v1f = [(m1
- m2)/(m1
+ m2)]v1o
Now we susbtitute this result back into the double-starred
equation:
v2f
= v1o + v1f = v1o + [(m1
- m2)/(m1
+ m2)]v1o = [(m1 + m2)/(m1
+ m2)]v1o + [(m1
- m2)/(m1
+ m2)]v1o = [2m1/(m1
+ m2)]v1o
as before. This solution is certainly shorter, but doesn't seem
to give us the 'no collision' solution discussed above.
Mastery Question
A clown juggles five balls while standing on a scale. He always
has
exactly one ball in one or the other hand. What is the average
reading on the scale?
Click here for the Solution.
Return to Notes Directory
Continue to Next Section
of Notes
D Baum 2000





